Diffusion Evolution Algorithm(DEA)の解説とPython実装
はじめに
Diffusion Models are Evolutionary Algorithmsの中で提案されたDiffusion Evolution Algorithmという最適化アルゴリズムの理解と検証のために記事を書きました。詳しい内容は元論文を参照していただければ幸いです。
論文の概要
論文では、拡散モデルと進化アルゴリズムの数学的等価性を示し、拡散モデルが本質的に進化アルゴリズムを実行していることを明らかにしています。進化をノイズ除去プロセスとみなし、逆進化を拡散とみなすことで、拡散モデルが選択、突然変異、生殖隔離などの進化アルゴリズムの要素を自然に包含していることを数学的に証明しています。そして,拡散モデルと進化アルゴリズムの等価性に基づいて、Diffusion Evolution Algorithmという新しい進化アルゴリズムを提案しています。
Diffusion Evolution Algorithm(DEA)
Diffusion Evolution Algorithm(DEA)は、進化アルゴリズムと拡散モデルを組み合わせた手法です。集団ベースの進化的な探索と、確率的な拡散過程による局所探索を行うため、グローバルな最適化問題にも効果的です。
この記事では、DEAのアルゴリズムを数式と共に解説し、Pythonでの実装を行います。最後に、最適化過程をアニメーションで可視化します。著者によるプログラムがGithubで公開されているため、実行だけを行いたい場合はそちらを参照ください。
アルゴリズムの概要
DEAは、個体群の進化を「拡散過程」として捉え、個体群がランダムなノイズを伴いながら進化し、最適解に向かって収束していきます。
1. 初期化
初期集団は、問題の解空間でランダムに初期化されます。各個体は以下のようにランダムなベクトルとして生成されます。
ここで、
2. フィットネス評価
次に、各個体のフィットネス(目的関数の値)を計算します。フィットネス関数
3. 拡散過程
DEAは、集団の各個体に対して以下の式を用いて、次世代の個体を生成します。
-
\alpha_t -
\hat{x}_0^{(i)} -
\sigma_t \epsilon_t^{(i)}
4. 高フィットネス個体の推定
各個体
ここで、フィットネススコアに基づく重み付き平均を計算します。
5. 進化の繰り返し
上記のプロセスを各世代ごとに繰り返し、集団を進化させていきます。最終的に、最適解に収束することを目指します。
PythonによるDEAの実装
それでは、実際にPythonでDEAを実装してみましょう。ここでは、Five-well potential function を最適化対象とします。
必要なライブラリのインポート
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
Five-well potential functionの定義
まず、最適化対象となる関数を定義します。今回は、複数の局所最適解を持つ Five-well potential function を使用します。
def five_well_potential(X):
x, y = X[0], X[1]
term1 = np.exp(-((x - 1)**2 + (y - 1)**2))
term2 = np.exp(-((x + 1)**2 + (y - 1)**2))
term3 = np.exp(-((x - 1)**2 + (y + 1)**2))
term4 = np.exp(-((x + 1)**2 + (y + 1)**2))
term5 = np.exp(-0.5 * (x**2 + y**2))
return - (term1 + term2 + term3 + term4 + term5)
DEAアルゴリズムの実装
次に、DEAの主要な部分を実装します。
Five-well poten
def diffusion_evolution(pop_size, dim, generations, fitness_func, alpha_schedule, sigma):
# 初期化 - 集団をランダムに生成
population = np.random.randn(pop_size, dim)*10 + 3
all_generations = [] # 全世代のデータを保存するリスト
for t in range(generations):
# フィットネス評価
fitness_scores = np.array([fitness_func(ind) for ind in population])
# アルファ値を取得
alpha_t = alpha_schedule(t, generations)
# 正規化定数Zを計算
Z = np.sum([np.exp(-fitness_scores[j]) for j in range(pop_size)])
new_population = []
for i in range(pop_size):
# 近傍の個体から推定される高フィットネス解を計算
neighbors = np.random.choice(range(pop_size), size=pop_size//2, replace=False)
weighted_avg = np.sum([population[j] * np.exp(-fitness_scores[j]) for j in neighbors], axis=0) / Z
noise = np.random.randn(dim) * sigma
new_ind = alpha_t * weighted_avg + (1 - alpha_t) * population[i] + noise
new_population.append(new_ind)
# 次世代の集団に置き換え
population = np.array(new_population)
# 全世代のデータを保存
for ind in population:
all_generations.append([t, ind[0], ind[1], fitness_func(ind)])
# データフレームに変換し保存
df = pd.DataFrame(all_generations, columns=['Generation', 'X', 'Y', 'Fitness'])
df.to_csv('gen.csv', index=False)
return population
パラメータの設定と実行
アルファ値のスケジュールやその他のパラメータを設定し、DEAを実行します。
pop_size = 50 # 集団サイズ
dim = 2 # 次元(2D)
generations = 100 # 世代数
sigma = 0.1 # ノイズの大きさ
def alpha_schedule(t, generations):
return 1 - t / generations
final_population = diffusion_evolution(pop_size, dim, generations, five_well_potential, alpha_schedule, sigma)
結果の可視化
結果をアニメーションで可視化します。
df = pd.read_csv('gen.csv')
fig, ax = plt.subplots()
X, Y = np.meshgrid(np.linspace(-3, 3, 100), np.linspace(-3, 3, 100))
Z = np.array([five_well_potential([x, y]) for x, y in zip(np.ravel(X), np.ravel(Y))])
Z = Z.reshape(X.shape)
contour = ax.contourf(X, Y, Z, levels=50, cmap='viridis')
scat = ax.scatter([], [], color='red')
cbar = fig.colorbar(contour)
cbar.set_label('Five-well Potential Value')
global_best = np.inf
def update(frame):
global global_best
current_gen = df[df['Generation'] == frame]
current_best = current_gen['Fitness'].min()
if current_best < global_best:
global_best = current_best
scat.set_offsets(current_gen[['X', 'Y']].values)
ax.set_title(f'Generation {frame} - Global Best Fitness: {global_best:.4f}')
return scat,
ani = FuncAnimation(fig, update, frames=range(generations), repeat=False)
ani.save('diffusion_evolution_five_well.gif', writer='imagemagick')
plt.show()
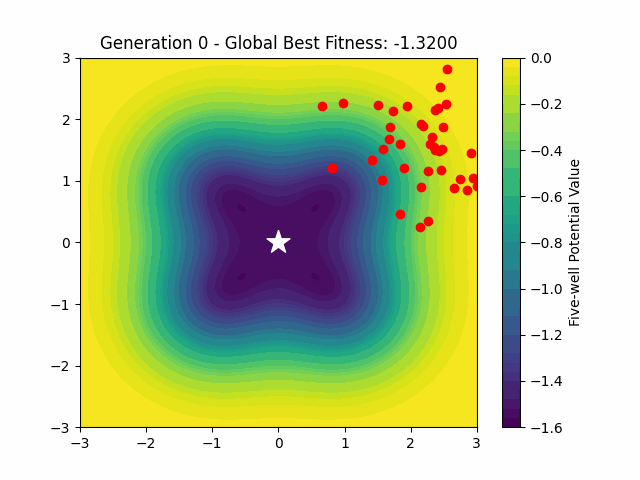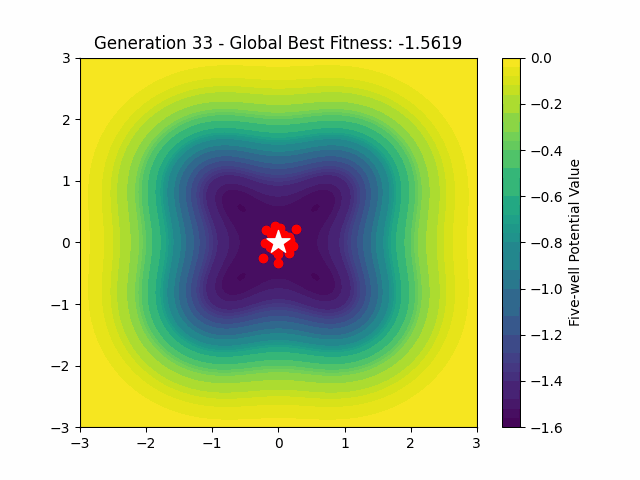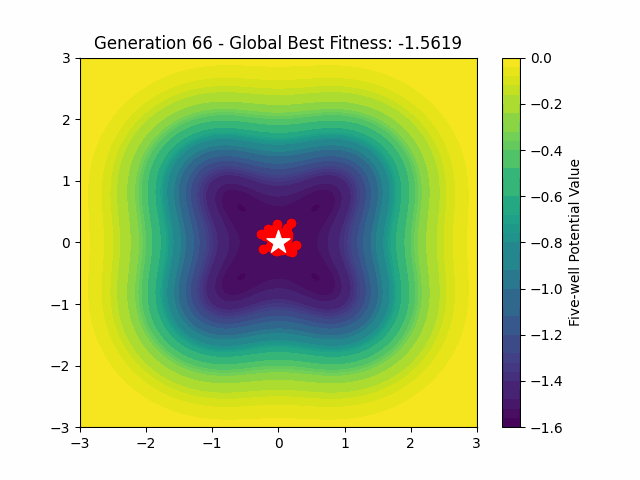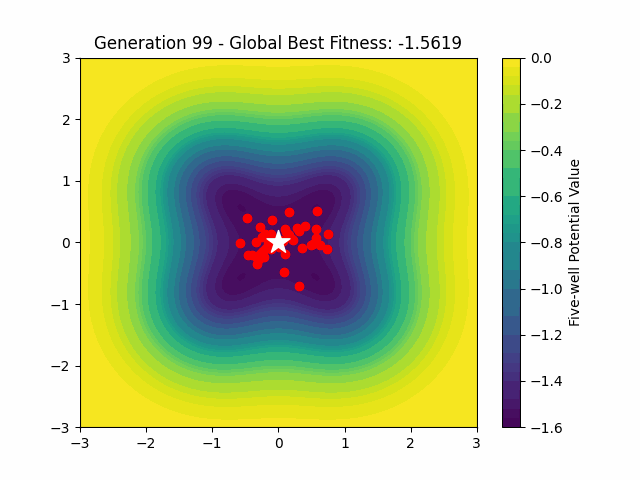
Discussion