Juliaで実装したルンゲ・クッタ法とDeffierentialEquations.jlでローレンツ方程式を計算して比べてみる。

自分で実装した４次のルンゲ・クッタ法と、常微分方程式ソルバーのDeffierentialEquations.jlでローレンツ方程式を計算して比べてる

ローレンツ方程式と設定条件

$$\begin{align}{} \frac{dx}{dt} = \sigma(y-x)\\\ \frac{dy}{dt} = x(\rho-z)-y\\\ \frac{dz}{dt} = xy - \beta z\end{align}$$

定数を

$${\sigma = 10, \beta = \frac{8}{3}, \rho = 28}$$

 初期値(x,y,z) = (1.1, 0.5, 0.5)とする

４次のルンゲ・クッタ法の実装

4次のルンゲ・クッタ法について整理するとこういう計算を行う

$${ y' = f(t,y), y(t_0)=y_0}$$

を考えるとき

$$\begin{align}{}&y_{n+1}=y_n+\frac{h}{6}(k_1+2k_2+2k_3+k_4)\\&t_{n+1}=t_n+h\\&k_1=f(t_n,y_n) \cr&k_2=f(t_n+\frac{h}{2},y_n+\frac{h}{2}k_1)\cr&k_3=f(t_n=\frac{h}{2},y_n+\frac{h}{2}k_3)\cr&k_4=f(t_n+h,y_n+hk_3)\end{align}$$

juliaで実装

ルンゲクッタ法の計算の心臓部を作る

function rk4(t,x,y,z,h)
    k1x = fx(t, x, y, z) * h
    k1y = fy(t, x, y, z) * h
    k1z = fz(t, x, y, z) * h
    k2x = fx(t + 0.5 * h,x + 0.5 * k1x,y + 0.5 * k1y,z + 0.5 * k1z) * h
    k2y = fy(t + 0.5 * h,x + 0.5 * k1x,y + 0.5 * k1y,z + 0.5 * k1z) * h
    k2z = fz(t + 0.5 * h,x + 0.5 * k1x,y + 0.5 * k1y,z + 0.5 * k1z) * h
    k3x = fx(t + 0.5 * h,x + 0.5 * k2x,y + 0.5 * k2y,z + 0.5 * k2z) * h
    k3y = fy(t + 0.5 * h,x + 0.5 * k2x,y + 0.5 * k2y,z + 0.5 * k2z) * h
    k3z = fz(t + 0.5 * h,x + 0.5 * k2x,y + 0.5 * k2y,z + 0.5 * k2z) * h
    k4x = fx(t + h, x + k3x, y + k3y, z + k3z) * h
    k4y = fx(t + h, x + k3x, y + k3y, z + k3z) * h
    k4z = fz(t + h, x + k3x, y + k3y, z + k3z) * h
    nx = x + (k1x + 2.0 * k2x + 2.0 * k3x + k4x) / 6.0
    ny = y + (k1y + 2.0 * k2y + 2.0 * k3y + k4y) / 6.0
    nz = z + (k1z + 2.0 * k2z + 2.0 * k3z + k4z) / 6.0
    return nx,ny,nz
end

次に計算を進めるための駆動部

function rungekutta(n,d,ic)
    t=0.0
    x0,y0,z0=ic
    x=[x0]
    y=[y0]
    z=[z0]
    for i=1:n
        nx,ny,nz = rk4(t,x[i],y[i],z[i],d)
        push!(x,nx)
        push!(y,ny)
        push!(z,nz)
        t=t+delta
    end
    return x,y,z
end

最後にローレンツ方程式を定義

function fx(t,x,y,z)
    a*(-x+y)
end
function fy(t,x,y,z)
    -x*z+b*x-y
end
function fz(t,x,y,z)
    x*y-z*c
end

実装した４次のルンゲ・クッタ法と微分方程式ソルバーDefferentialEquations.jlとの比較

ルンゲ・クッタ法の実装ができたので、ここからは実際に計算して比較していく

実装ルンゲ・クッタ法でローレンツ方程式を計算

後のDifferentialEquations.jlとの比較のため要素数を6,595にした。それを単純にステップ数で割り算したので変化量が0.018で計算

a = 10.0
b=28.0
c =8/3
ic = (1.1,0.5,0.5)
x,y,z =rungekutta(6594,0.018,ic)

グラフを描画するとこの様になる

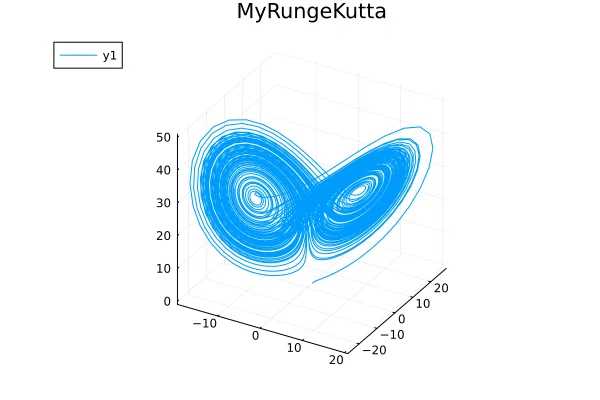
少しカクついてるけど、発散したりせずにある程度求めらている。

DifferentialEquations.jlでローレンツ方程式を計算

DifferentialEquations.jlでローレンツ方程式を計算
これは、DifferentialEquations.jlのチュートリアルにも出てくるのとほぼ同じ

using DifferentialEquations
function lorenz!(du,u,p,t)
    du[1] = 10.0 * (u[2]-u[1])
    du[2] = u[1]*(28.0-u[3])-u[2]
    du[3] = u[1]*u[2]-(8/3)*u[3]
end

u0=[1.1;0.5;0.5]
tspan = (0.0,500.0)
prob = ODEProblem(lorenz!,u0,tspan)
sol=solve(prob)

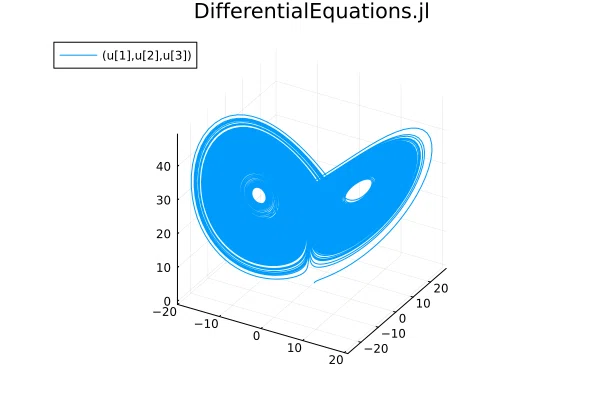
美しい。
さすが、計算パッケージだけある。よくできている。

両者比較

それぞれで求めてみて、パットした見た目だけではなく、違う側面からも観察してみる
ｘの推移をグラフにしてみた

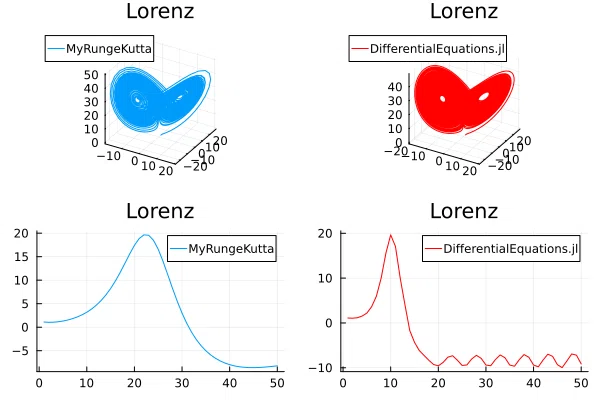
だいぶ違う。
細かい作りが違うので、すべての条件を揃えるわけにはいかなかった。
さすがパッケージはよくできていると思う。

それと同時にルンゲ・クッタ法っていう数値計算の入門出でてくる方法を浸かってもしっかり計算できることを確認できた。

パッケージを使うのもよいが、こうやって、自分で実装してみることでより理解が深まると思う。