Zenn
📈

Pythonを使って時系列分析を丁寧に Part.1（時系列分析のモデル、周期成分、自己相関）

2023/01/29に公開
Python
#
時系列分析
#
statsmodels
tech

時系列分析

時系列データは

  • トレンド
  • 季節成分
  • 不規則成分

の3要素が合成している、と考えるのが一般的です。

合成の仕方は2通りが考えられ

  • 加法モデル
  • 乗法モデル

です。

モデルの定式化

トレンドをT(t)、規則成分をS(t)、不規則（Irregular）成分をI(t)として、元データO(t)を表すことを考えてみます。
加法モデルであれば、そりゃ

\begin{align*} O(t) = T(t) + S(t) + I(t) \end{align*}

となりますね。乗法モデルであればもちろん

\begin{align*} O(t) = T(t) \times S(t) \times I(t) \end{align*}

周期成分の発見

周期成とは何でしょうか。
例えばアイスクリームの販売数とかで考えると、毎年夏に売れることが想像できます。

毎年夏に特別な振る舞いを示す → 周期成がある

とみなすわけですね。これを機械的に見分けるためにはどうすればよいでしょうか。

例えば月ごとの時系列データy(t)があるとして、毎年夏に売れるという特徴を持つのであれば
y(t)とy(t-12)が値として近いことになります。
近いかどうかを判断するのは差分を導入すれば良いので、それを全てのtで計算して和を取って見ればよいわけです。
あ、和を取るとy(t)とy(t-12)が正でずれるときと負でずれるときで相殺してしまうので、二乗和を取りましょう。
つまり、12ヶ月の周期性があるかどうかを判断できる値A(12)は

A(12) = \sum_t \left(y(t) - y(t-12)\right)^2

として定義でき、このA(k)が小さくなる k で周期性があると見なせることになります。
適当に作ったデータで見てみましょう。

y = [0,0,0,0,0,1,2,3,2,1,0,0,0,0,0,0,0,1,2,3,2,1,0,0]

これは 1月から翌年12月までの、疑似アイスクリーム販売数だとしていまして、
6月に1個、7月に2個、8月に3個、9月に2個、10月に1個、ほかは0個としています。
これでA(k)を計算してみましょう。
今回は一旦12ヶ月までのデータをみるとしてみます。

A = [0 for _ in range(13)]
for k in range(13):
    for t in range(len(y)):
        A[k] += (y[t] - y[t-k])**2

これで求めたAを見てみると

print(A)

[0, 12, 36, 60, 72, 76, 76, 76, 72, 60, 36, 12, 0]

となっており、A[0]（自分自身との差をとっているので当然）、A[12]で0になっていますね。

これでも良いと言えば良いんですが、もっと標準的に使いやすい指標として自己相関（autocorrelation）があります。y(t)の平均を\bar{y}として、

A(k) = \dfrac{\sum_{t=k+1}^{T}(y(t)-\bar{y})(y(t-k)-\bar{y})}{\sum_{t=1}^T(y(t)-\bar{y})^2}

となります。自己相関というだけあって、相関係数と似ていますね。

相関係数 = \dfrac{\frac{1}{n}\sum_{i}^{n}(x_{i}-\bar{x})(y_{i}-\bar{y})}{\sqrt{\frac{1}{n}\sum_{t=i}^n(x_{i}-\bar{x})^2}\sqrt{\frac{1}{n}\sum_{t=i}^n(y_{i}-\bar{y})^2}}

これを実際に計算してみましょう。

A = [0 for _ in range(15)]
for k in range(15):
    bottom = 0
    for t in range(0,len(y)):
        bottom += (y[t]-y_bar)**2

    top = 0
    for t in range(k,len(y)):
        top += (y[t] - y_bar)*(y[t-k] - y_bar)
        
    A[k] = top/bottom

図示してみると

from matplotlib import pyplot as plt
# 日本語フォント
plt.rcParams['font.family'] = 'Hiragino Sans'

# 横軸
K = [i for i in range(15)]

fig, (ax) = plt.subplots(1,1,figsize=(6,4))

ax.set_xlabel("k")
ax.set_ylabel("自己相関")
ax.plot(K,A)

あれ、おかしくないですか？
A(12) = 1ではないですね。
ここでよくよく定義式を見てみると、分子の範囲が k+1 \leqq t \leqq T となっていて、t = 0 から始まっていないですね。
これを1に近づけようとすると、データのサイズを大きくするしかないです。
ですが、どちらにしろ、kが大きくなればなるほどA(k)の値は小さく見積もられてしまうことに注意が必要です。
見方として ピークが存在しているかどうか で判断するのが良さそうです。

statsmodelsを使ってみる：二酸化炭素濃度の例

気象庁が出している二酸化炭素濃度の月平均値[1]を例にしてみましょう。

ページ下部にcsvファイルがあります。
このcsvファイルは下部に注意事項が書いてあるため直接ロード出来ないことに注意してください。
（下部を削除するなどしてください）

Pythonのstatsmodels[2]を使って自己相関を図示してみます。

import pandas as pd
import datetime
import statsmodels.api as sm

# pathは各々で指定してください
df = pd.read_csv(path)
y = df.iloc[:250]
# 型指定
y = o[["二酸化炭素濃度の月平均値"]].astype("float")

# 自己相関を図示、36点まで
sm.graphics.tsa.plot_acf(y,lags=36)

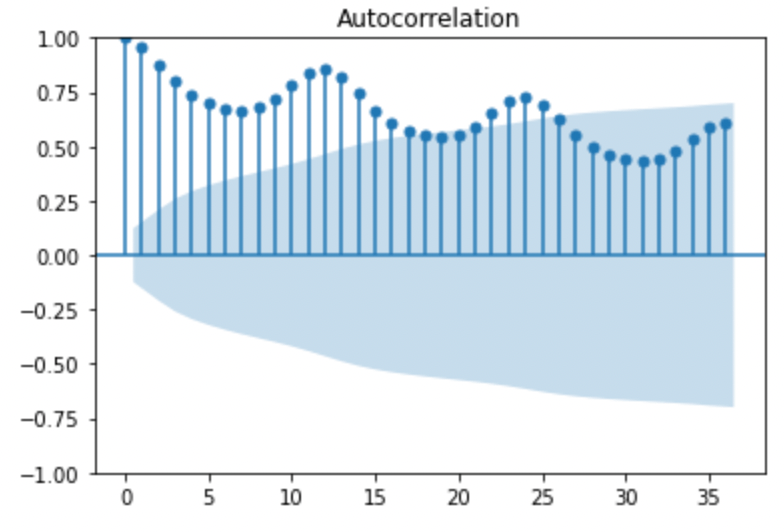
これをみれば12,24,36にピークが来ていることがわかり、（元データは1ヶ月ごとの数値なので）12ヶ月の周期性が存在していることがわかりますね。

このこと（12,24,36の件）をもう少し詳しく見てみましょう。
この現象を言い換えると、12ヶ月の周期性があることを理由に24ヶ月の周期性が存在している、ということになります。
24ヶ月の周期性があるかもしれないのに、12ヶ月の周期性があることで見えづらくなっている
と捉えることも出来ます。

  • 12ヶ月の周期性に起因しており、本当は24ヶ月での周期性はない
  • 12ヶ月の周期性とは別に24ヶ月の周期性が存在している
    • 24ヶ月の周期性 = 去年の値には依存しないが、一昨年の値には依存する

このどちらなのかを見極めたい、ということです。
そこで偏自己相関が登場します。

偏自己相関（ここでは紹介だけ）

変自己相関の計算を手でやりだすととんでもないことになるのでそれは別でやるとして、y(t)とy(t-k)の関係を、y(t-1), y(t-2), \cdots , y(t-k-1)の影響を取り除いて計算したものです。
Pythonのstatsmodelsを使うとすぐ出来ます。

sm.graphics.tsa.plot_pacf(y,lags=36)

これを見ると１ヶ月は強く、2ヶ月周期が弱く、12ヶ月周期性がそこそこの強さで存在していることがわかります。

脚注

  1. https://www.data.jma.go.jp/ghg/kanshi/obs/co2_monthave_ryo.html ↩︎

  2. https://www.statsmodels.org/stable/index.html ↩︎

Discussion