ベイズ推定を使って、連続殺人犯の居場所を解明しよう！　(Numb3rsより)

概要

今から２０年くらい前に「Numb3rs～天才数学者の事件ファイル～」という、天才数学者とFBI捜査官のコンビが難事件を解決していくアメリカドラマが放送されていた。その中で出てきたエピソードの１つに、連続殺人の居場所をこれまでの殺害現場から推測する、所謂、地理的プロファイリングが使われるエピソードがあった。
　今回は、この問題を地理的プロファイリングで使われている主流の方法とは別のベイズ推定方法を用いてアプローチしてみようと思う。

注意事項

• わかりやすさのため、数学的厳密性を犠牲にしています。
• 実際の地理的プロファイリングではありません、あくまで、ベイズ推定の応用問題として面白いと思ったので考えました。確立された地理的プロファイリングを学びたい方は、例えば、日本語の本だと「地理的プロファイリング」（北大路書籍）や論文を読むことをお勧めします。

ベイズ推定について

事前知識として、一応、ベイズ推定について記載する。
だが、本記事はベイズ推定の解説がメインではないので、詳細は別の解説記事を見てほしい。

0. 真の分布$q(x)$から出たデータ$x^n = (x_1, x_2, x_3, ..., x_n)$を集める
   補足説明

   • ベイズ推定では、データがある分布$q(x)$から出てくるものと仮定する
   • 私たち（推測者）は、この分布$q(x)$を見ることはできないが、そこから出るデータ$x^n$はみることができる
   • こういった制約の中で、データの背後にある真の分布$q(x)$を推測しようというのがベイズ推定の問題設定だ
1. 確率モデル$p(x|w)$と事前分布$\psi (w)$を設定する
   補足説明

   • 私たち(推測者)は、データ$x^n$や問題背景（今回の場合、連続殺人事件）から、背後にある真の分布$q(x)$がどのような分布か予測し、それを表す最適な確率モデル$p(x|w)$を、直感や経験から設定する。
   • つまり、私たち(推測者)は、確率モデル$p(x|w)$の$w$をうまく調節すれば、それが真の分布$q(x)$になるであろうことを期待して確率モデルを設定する。
   • 同様に確率モデル$p(x|w)$のパラメータ$w$の事前分布$\psi (w)$を決める。
2. 観測したデータ$x^n$と先ほど用意した確率モデル$p(x|w)$、事前分布$\psi (w)$を使って、事後分布を計算する。

確率モデル$p(x|w)$

今回、連続殺人犯の事件現場と住居の関係性を表す式を真の分布と確率モデルに設定したい。

ざっくり、以下の２つの性質を持っていれば良さそうである。

1. 住居から近すぎる場所では、犯罪を起こさない（なぜなら、すぐバレちゃうから）
2. 住居からあまりにも遠く離れた場所でも、犯罪を起こさない（なぜなら、犯行は習慣化しており、遠くまで行くのが面倒だから）
3. 殺人犯は住居と職場の２カ所を拠点にしている

補足説明

• １つ目と２つ目の条件は、私が勝手に考え、３つ目の条件は、ドラマの設定から持ってきた。
• 実際に使われている地理的プロファイリングの要素はこれよりはるかに複雑だが、今回は、一種の遊びでやるので、上記のような適当な設定にした。

そこで、テキトーに、この３つの性質をもつ、座標$(x,y)$で事件の発生確率表すモデル$p(x, y|a_i, b_i, c_i, d)$を以下のように考えた。

$$p(x, y \mid a_1, a_2, b_1, b_2, c_1, c_2, d ) := \frac {1} {V} \sum_{j=1}^2 \frac { a_j \exp(-0.05 D_{j}(x, y))} { 10 + \left | D_{j}(x, y) - d \right | }$$

ただし、$a_1 + a_2 = 1$を満たし、$D_{j}(x,y)$は住居又は職場からの距離、つまり、$D_{j}(x,y):= \sqrt{ \left ( x - b_j \right )^2 + \left ( y - c_j \right )^2 }$であるとする。また、$V$は正規化定数であり、$x,y$で積分した結果が$1$になるようにする。
また、慣例的に${\bf x} = (x, y)$, $w = (a_1, a_2, b_1, b_2, c_1, c_2, d)$と書くものとする。つまり、確率モデルはすべてのパラメータを明示的に記載するのではなく、$p({\bf x}|w)$と短くに書くものとする。

定数についての補足説明

• 上記の10や0.05などの定数は後々、グラフの見やすさのため、決めた適当な値であり、重要ではない
• $V$を具体的に数式で書くと以下のようになる。
  • $V := \int_{\bf x} p({\bf x} \mid w ) d{\bf x}$

パラメータに関する補足説明

• $(b_1, c_1)$は犯人の職場の座標を表し、$(b_2, c_2)$は住居の座標を表す。
• $a_1$は職場から犯罪を起こす比率、$a_2$は住居から犯罪を起こす比率とした
• $d$は犯人が拠点から最も犯罪を起こしやすいと感じる距離とした。

事前分布$\psi (w)$

事前分布は今回すべて、一様分布とする。
しかし、ある程度区間を決める必要はあり、今回、座標については$[0, 80] \times [0, 80]$の閉区間、$a_1$については$[0, 0.45]$、　$d$については$[0, 14.5]$の閉区間の中で一様に確からしいと仮定する。

a1についての補足説明

• $a_1$は本来、$0\sim 1$の範囲の値をとることができるが、今回はモデルの対称性を崩すため、意図的に$0\sim 0.45$の範囲をとることにした。
• モデルが対称性を持つ場合、シミュレーションが不安定になることがある。理由はその数学的構造にあるのだが、今回は立ち入らない。

真の分布$q(x)$とデータ$x^n$

さて、本来の手順と逆になるが、今回は真の分布を、確率モデルのパラメータが$a=0.35$, $(b_1, c_1) = (28,28)$, $(b_2, c_2) = (52, 48)$, $d=7.2$とした。
この分布をプログラムにプロットしたのが以下だ。

パラメータに関する補足説明

• これらの値は、私がグラフなどがきれいに見えるように決めた値であり、意味のある数値ではない。

グラフに関する補足説明

• このグラフはヒートマップで、明るい部分の確率が高く、暗い部分の確率が低い。
• 右上のドーナッツの穴の中心部分が住居であり、左下のドーナッツの穴の中心部分が職場である。

数値計算について

• この記事の数値計算はすべて区分求積法で計算しているが、次元の呪いで計算量が爆発的に増えていくためお勧めできない。

この真の分布$q(x)$から、データをランダムに３０個とってくると以下のようなデータが得られた。

これだけだとわかりにくいので、先ほどの真の分布と重ねてみる。

こうしてみると、確かに真の分布から生成されていることがわかる。
このように、人の目で犯人の犯罪行為の規則性を見つけることは簡単ではない。

事後分布$p(w|X^n)$を計算

まず、事後分布を計算する準備として、事前分布$\psi ( w)$、確率モデル$p({\bf x}|w)$、データ$x^n$を使って尤度関数を以下のように計算する。

$$L(w) := \psi ( w) \prod_{i=1}^N p({\bf x}_i \mid w )$$

この式を見てわかる通り、尤度関数は事前分布$\psi ( w)$と確率モデル$p({\bf x}|w)$にデータ$x^n$を代入して、かけ合わるだけでよい。

尤度関数の意味

• 尤度関数の意味というのを語弊を恐れず、ざっくり言ってしまうと、パラメータ$w$がどれだけ真のパラメータに近いか、ということを表す関数。
• この性質から、尤度関数が高いパラメータがよく出るような確率分布を作れば、それが真のパラメータを予測する分布になっていることが期待できる。そして、それこそが次に紹介する事後分布$p(w|x^n)$だ。

事後分布$p(w|{\bf x}^n)$は以下のように計算できる

$$p(w|x^n) = \frac{1}{U} L(w)$$

ここでUは正規化定数で、積分の結果が１になるように設定する。

補足説明

強いてUを数式で書くと以下のような形になるが、合計を1にするためだけの定数であり、本質的ではないのであまり気にする必要はない。

$$U = \int_w L(w) dw$$

上記の数式に従い、数値計算をすると、$p(w|x^n)$を導くことができる。
$p(w|{\bf x}^n)$は、$w$が$w = (a_1, a_2, b_1, b_2, c_1, c_2, d)$であることから、７次元（より正確には$a_1+a_2=1$という制約より６次元）空間上の確率分布であり、３次元以下しか認知できない人間には”見る”ことができない。しかし、以下のように見たいパラメータ以外を積分して強制的に２次元に落とし込んでやれば、可視化することができる。

例：職場$(b_1, c_1)$の事後分布を可視化する式

$$p(b_1, c_1 | {\bf x}^n) = \int_{a_1, a_2, b_2, c_2, d} p(a_1, a_2, b_1, b_2, c_1, c_2, d |{\bf x}^n) \ da_1 da_2 db_2 dc_2 dd$$

この方法を使って、職場$(b_1, c_1)$と住居$(b_2, c_2)$を可視化してみる

職場$(b_1, c_1)$の事後分布

職場の事後分布を真の分布と重ねて描画した（カクカクしていて荒い部分が事後分布）。

白→黄→赤→黒の順で確率が低くなっていく。
グラフから、大体、職場の少し上あたりの確率が高くなっていることが確認できる。

住居$(b_2, c_2)$の事後分布

同様に住居の事後分布を真の分布と重ねて描画した

こちらも、住居の少し上あたりの確率が高くなっていることが確認できる。

比率$a_1$の事後分布

真の分布の$a_1$は$0.35$であるため、よい推定になっていることがわかる。

犯人が犯罪を起こしやすいと考えている距離$d$の事後分布

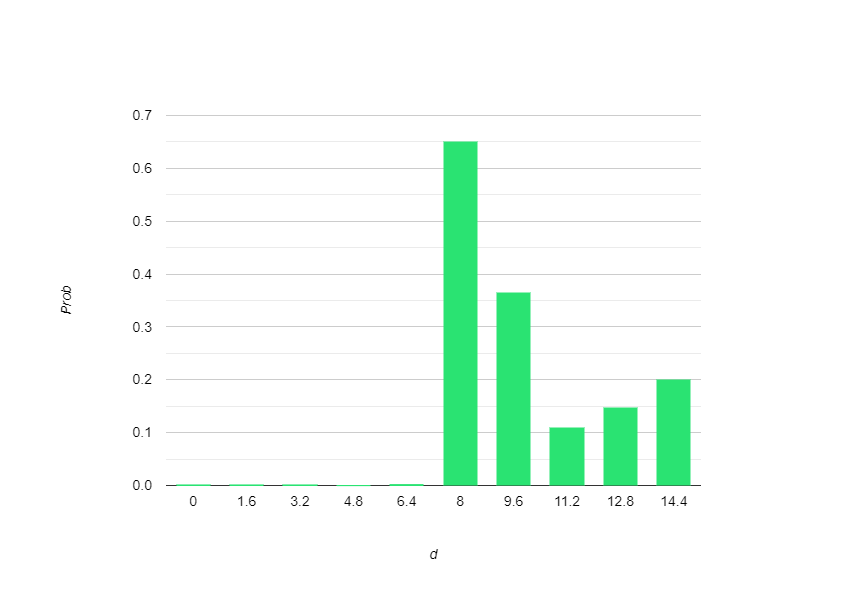
真の分布の$d$は$7.2$であるため、こちらもよい推定になっていることがわかる。

予測分布・モデル選択

犯人の居場所を特定できたのでほとんど目的を達成することができたが、せっかくなので、さらに分析を進めたいと思う。

予測分布

事後分布$p(w |{\bf x}^n)$を使って、確率モデル$p({\bf x}| w)$を$w$について積分することで、真の分布$q({\bf x})$を予測する分布、つまり、予測分布$p^*({\bf x})$を作ることができる。

$$p^* ({\bf x}) = \int_w p({\bf x} | w) p(w | {\bf x}^n) dw$$

これを数値計算して求めたのが以下の図である。左の図が真の分布で、右の図が予測分布である。

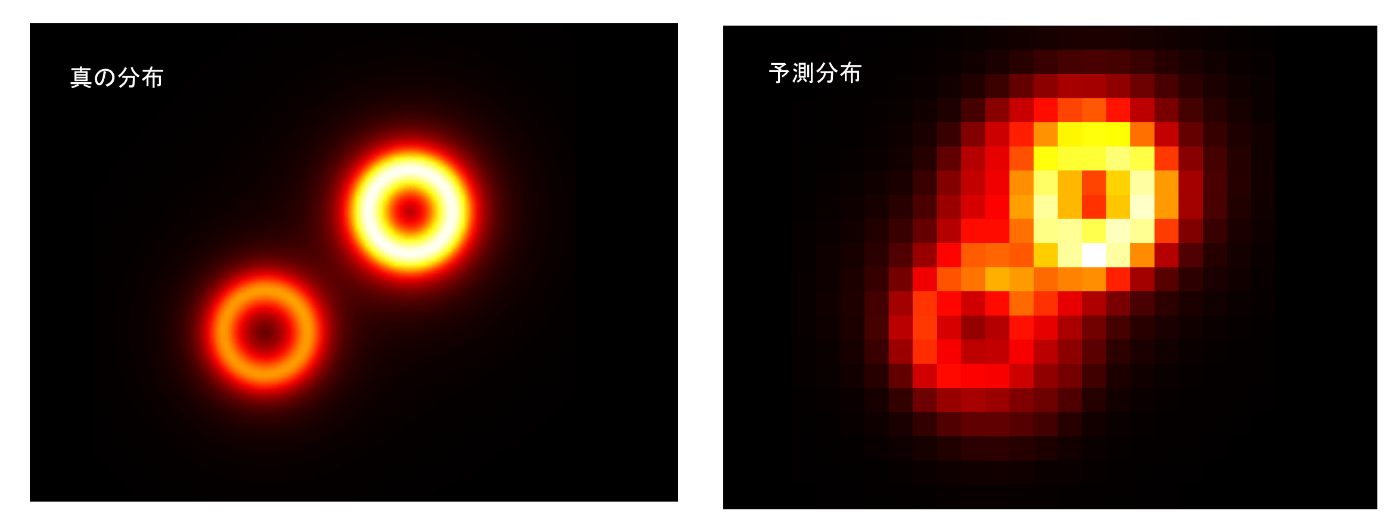
こうして見比べてと、少し予測分布のほうが幅が広く、上に位置していることがわかる。

この予測分布を使って、犯人の次の犯行現場を予想することができるだろう。
もっとも、予測については深層学習を使ったほうが良い結果が出る（たぶん？）ので、今はあまり使われないと思う。

モデル選択

ドラマにおいて、天才数学者は最初、犯人が２つの拠点（住居と職場）を利用していることに気が付かず、「犯人は１つの拠点から犯行を行っている」という誤った仮説のもとで、数式を立てた。その結果、正しい事後分布にならず、犯人を逮捕することができなかった。
　しかし、その挫折を、兄のFBI捜査官や父と協力して、乗り越え、再度挑戦するというのが、ドラマのクライマックスだ（唐突なネタバレ）。
　ドラマの中では、犯人の拠点が２つある可能性に気が付いた瞬間、これまでの「犯人の拠点が１つである」という仮定のモデルを棄却して、すぐに「犯人の拠点が２つある」というモデルを採択した。
　これを直感ではなく、もう少し統計的に判断するならば、統計モデルのモデル選択をすることになる。
つまり、真の分布と計算したモデルの誤差を推測する量である情報量基準という値を計算し、比べて、情報量基準が小さいほうが良いモデルだ、ということになる。

情報量基準のすごさ

• 情報量基準の説明で、「真の分布と計算したモデルの誤差を推測する量」といったが、この情報量基準のすごい点は、なんと、計算には真の分布が必要ない、という点だ。
• 例えば、「ボールペンと鉛筆の長さを比較したとき、鉛筆はどれくらい長いか、予想してください。しかし、あなたに考える材料として鉛筆は渡せるけど、ボールペンは渡せません。」と言われたら途方に暮れてしまうだろう。しかし、情報量基準は”ボールペン”がなくてもどれくらい長いか回答できてしまう、という驚異的な式だ。
• もちろん、しっかりカラクリがある。真の分布を使わない代わりに、そこから出たデータを使って推測するのだ。前の例だと、ボールペンの部品だけは渡してくれるようなものである。

情報量基準はいろいろあるけど、現在のところ最強の基準はWAIC（またはWBIC）であるので、今回はこれを利用する。

$$WAIC = - \frac {1} {n} \sum_{i=1}^n \log p^*(x_i | w) + \frac {1} {n} \sum_{i=1}^n \left ( \int_w (\log p(x_i | w))^2 p(w|x^n) dw - \left ( \int_w \log p(x_i | w) p(w|x^n) dw \right )^2 \right )$$

事後分布で平均をとっているので、かなり計算コストが高い式なのだが、頑張って計算すると、以下のような値になった。
（ついでに、「１つの拠点から犯行を行っている」という誤った仮説の下でモデルを作り、事後分布をつくり、それのWAICも計算した）

モデル	WAIC
２つの拠点から犯行を行うモデル(これまで計算してきたモデル)	5.32
１つの拠点から犯行を行うモデル	5.55

１つの拠点から犯行を行うモデル

• このモデルの記述は難しくない。具体的には以下の形になる

  $$p(x, y \mid b_1, c_1, d ) := \frac {1} {V} \frac { \exp(-0.05 D(x, y))} { 10 + \left | D(x, y) - d \right | }$$

  ただし、$D(x, y) := \sqrt{ \left ( x - b_1 \right )^2 + \left ( y - c_1 \right )^2 }$である。

• $b_1, c_1, d$の事前分布は同じでよい

この結果から、「２つの拠点から犯行を行うモデル(これまで計算してきたモデル)」のほうが妥当である、といえる。

結論

• ベイズ推定と仮想的な確率モデルを使って、犯人の居場所を特定する、という遊びをやってみた
• 計算してみると、サンプル数３０で、ようやく、「２つの拠点から犯行を行うモデル(これまで計算してきたモデル)」のほうが妥当である、という結論に到達しているのに、ドラマの中ではより少ないサンプル数で、拠点が１つでないことに気が付いており、天才数学者とFBI捜査官の最強コンビは、尋常じゃないことがよくわかった。
• 今回、区分求積法ですべて数値計算をしたが、次元の呪いで半分死にかけたので、次回はPyMC（マルコフ連鎖モンテカルロ法）を使いたい（反省）

最後に

• 「Numb3rs 天才数学者の事件ファイル」は２０年前の古いドラマですけど、面白いので、ぜひ皆さんにもおすすめです、それではまた！