Claude 3.7 Sonnetの拡張思考モードにおったまげた件
I.はじめに
昨日2025年2月25日、Anthropic社はClaude 3.7 SonnetとClaude Code(プレビュー版)をリリースしました[1]。
素晴らしく未来を感じさせるものでしたので、感動を共有するために速報記事をしたためました。
※本記事はあくまで筆者一個人の見解によるものであることをご了承ください。また、検証には私物のClaudeアカウントを利用しました。
II.リリースの概要
発表のあったClaude 3.7 SonnetとClaude Codeについて簡単にご紹介します。
(1)Claude 3.7 Sonnet
- Claude 3.5 Sonnetの後継モデルにあたり、数学・CS・コーディング支援分野で大きな性能向上を果たす
- 必要に応じて拡張思考モード(extended thinking mode)を使用することができ、より精緻に問題解決を考えさせるとともにモデルの思考過程を出力させることができる
- コンテクストウィンドウサイズは200k[2]であり、3.5 Sonnet他Claudeファミリーの各モデルと同じ
- Amazon Bedrockでは現状米国3リージョンのみ対応。フルリージョン対応は今後予定される[3]
また、アナウンスには以下のコメントがあり、今後のAnthropic社/Claudeの展望を感じさせられるものでした。
"Just as humans use a single brain for both quick responses and deep reflection, we believe reasoning should be an integrated capability of frontier models rather than a separate model entirely." [1:1]
(引用者訳:人間がちょっとした振り返りと深い内省を両方できるように、推論とは先進モデルの統合的な能力の1つであるべきであって、単個のモデルとして存在するべきものではない。)
個人的には、ClaudeファミリーはLLMを通じたシームレスなユーザー体験を第一において開発されているのだなと解釈しました。既に市場にあるGemini 2.0 Flashなどでは100万トークンが扱えますし[4]、モデルスペックで勝負するというよりはあくまで使いやすいインターフェースを追求されている印象です。
(2)Claude Code
Claude Codeはリサーチプレビュー機能(いわゆるベータ版、正式リリース前機能)としてアナウンスされたもので、なんとターミナルから対話型インターフェースを起動してClaudeを操作し、ファイルを操作してもらえるというものです。
こちらはまた後日改めて記事を書きたいので本稿のスコープ外としますが、実際の挙動は以下の公式動画で確認できます。
Next.jsのプロジェクトファイルを開き、ソースコードの概要から新機能の開発まで行ってくれるようです。(なんという未来...)
III.標準モード と 拡張思考モードをそれぞれ使ってみた
Claude 3.7 Sonnetの標準モードと拡張思考モードの性能を比較するために、分析プロジェクトで実際に遭遇した課題をアレンジし与えてみました。
題:「N次元空間内の点Pから球を描き、他の点をちょうどk個含めるための半径rを導出してください」
まず標準モードでの実行結果ですが、20秒ほどで以下のコードが出力されました。(関数の呼び出し部分は省略しています。以降同)
import numpy as np
from scipy.spatial import distance
def find_radius_containing_k_points(points, center_point, k):
"""
N次元空間の点Pから球を描き、他の点をちょうどk個含めるための半径rを導出する関数
Parameters:
----------
points : numpy.ndarray
N次元空間上の点群のリスト(形状: [点の数, 次元数])
center_point : numpy.ndarray
中心点P(形状: [次元数])
k : int
含めたい点の数
Returns:
----------
radius : float
ちょうどk個の点を含む球の半径
"""
# 中心点と同じ点がpointsリストに含まれる場合を考慮する
# 中心点と完全に一致する点を除外
points_without_center = []
for point in points:
# 浮動小数点の誤差を考慮した等価性チェック
if not np.array_equal(point, center_point):
points_without_center.append(point)
points_without_center = np.array(points_without_center)
# 中心点からの距離を計算
distances = np.array([distance.euclidean(center_point, point) for point in points_without_center])
# 距離を昇順でソート
sorted_distances = np.sort(distances)
# k個の点を含める場合、k番目の点までの距離が半径となる
if k <= len(sorted_distances):
radius = sorted_distances[k-1]
else:
raise ValueError(f"k={k}は点の総数を超えています。点の数は{len(sorted_distances)}個です。")
return radius
このfind_radius_containing_k_points関数は確かに動作するのですが、点Pから同一距離に複数の点が存在し、ちょうどk個を囲うことができない(取りすぎてしまう)ケースでは期待する出力が得られません。
それでは拡張思考モードではどうでしょうか。こちらは推論に2分2秒かかり、以下が出力されました。
import numpy as np
def find_sphere_radius(P, points, k):
"""
N次元空間の点Pから球を描き、他の点をちょうどk個含めるための半径rを導出する
引数:
P: 球の中心点を表すnumpy配列(N次元)
points: 他の点の集合を表すnumpy配列(形状は[m, n]、mは点の数、nは次元数)
k: 球内に含めたい点の数
戻り値:
球の中心Pからの距離がrの範囲内にちょうどk個の点が存在するような半径r
そのような半径が存在しない場合はNoneを返す
"""
# Pから全ての点までのユークリッド距離を計算
distances = np.sqrt(np.sum((points - P)**2, axis=1))
# 点Pが点集合に含まれている場合、その点を除外(距離≒0の点)
mask = ~np.isclose(distances, 0)
if np.sum(mask) < len(distances):
distances = distances[mask]
# 境界条件のチェック
if k <= 0:
return 0
if k > len(distances):
return None # 十分な点がない
# 浮動小数点の誤差を避けるために距離を丸め、一意な距離を取得
unique_distances, inverse_indices, counts = np.unique(
np.round(distances, decimals=10),
return_inverse=True,
return_counts=True
)
# 各一意な距離における累積点数を計算
cumulative_counts = np.cumsum(counts)
# ちょうどk個の点を与える一意な距離のインデックスを見つける
exact_k_indices = np.where(cumulative_counts == k)[0]
if len(exact_k_indices) > 0:
# ちょうどk個の点を含む距離が見つかった
return unique_distances[exact_k_indices[0]]
else:
# ちょうどk個の点を含む距離は存在しない
return None
一見すると同じようなコードですが、こちらはnp.uniqueを用いて同一距離上の点が複数あった場合を考慮しており、条件を満たす距離rが存在しない場合が明確に考慮されています。
またこの拡張思考モードですが、Sonnetさん(もはやそう呼びたい)がその思考過程で「あーでもないこーでもない」としているのをリアルタイムで確認することができます。(下図赤枠囲い箇所)
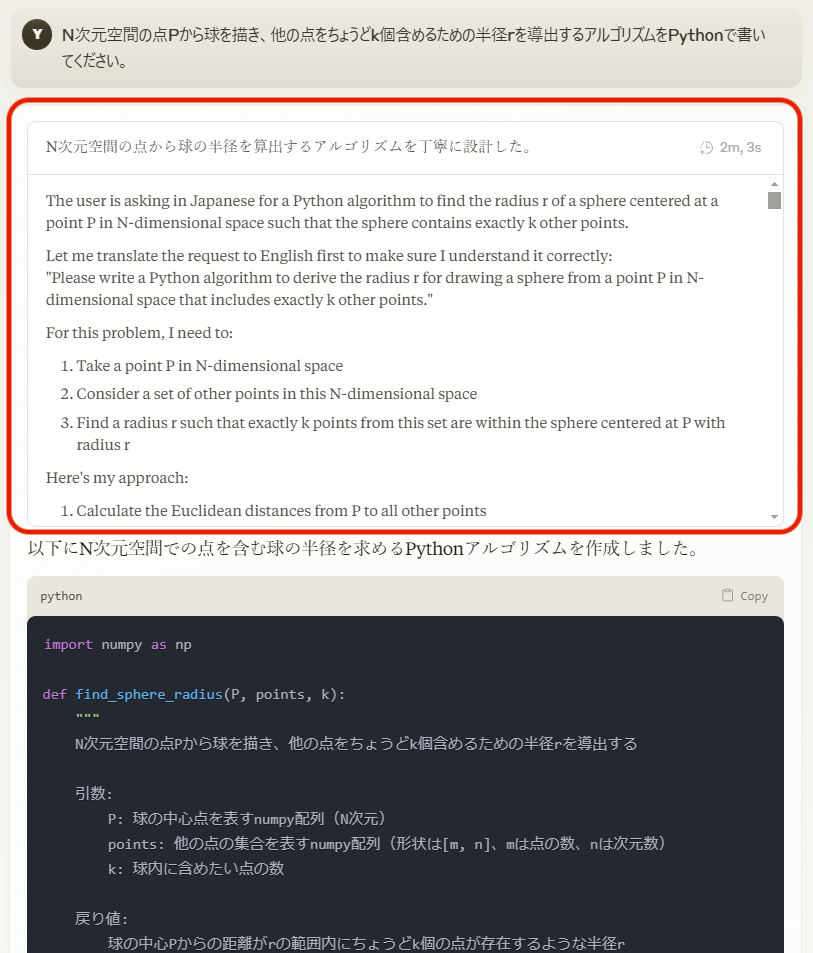
驚いたのは以下の内容でした。実際の出力からの引用です。
Actually, the problem statement specifically asks for a sphere that contains "exactly k other points", which implies that P is not counted among these k points. So let me simplify the solution(...)
(引用者訳:ちょうどk個の点が、と指示されているから、暗に中心の点P自体はk個に含めないということなのではないか?これを踏まえて問題を単純化してみよう(...))
But there's still another issue to consider. What if there are multiple points at the same distance from P? In that case, we need to be careful about the "exactly k points" requirement.
(引用者訳:ちょっと待った、もし複数の点が点Pから同一距離にあったらどうするんだ?この場合「ちょうどk個」という条件について注意する必要がありそうだ。)
実際に人間が複数名集まって行われているかのような、与えられた課題に対する高度に分析的な議論がなされており、3.7 Sonnetの高度な推論能力が確認できます。
IV.まとめ
Anthropic社のClaude 3.7 Sonnet / Claude Codeの発表アナウンスの概説と、3.7 Sonnetの目玉機能「Extended thinking mode」の実行テストを行いました。
拡張機能モードは、「正しそうなLLMの出力が本当に合っていそうなのかどうか」を人間が人間的に考えるためのヒントを与える、強力なツールだと実感しました。
採用情報
D2Cグループではデータサイエンティスト、エンジニアの方々を募集しています。
ブログを読んでD2Cで働いてみたいと思った方、D2Cの業務に興味をもってくださった方がいらっしゃいましたら是非ご応募ください。
▼ D2Cグループ採用サイトはこちら
▼ D2C問い合わせフォームはこちら
-
前述のアナウンスページにcontext window sizeの記載は見当たりませんでしたが、モデル概要ページに記載があります: https://docs.anthropic.com/ja/docs/about-claude/models/all-models ↩︎
-
https://aws.amazon.com/jp/blogs/aws/anthropics-claude-3-7-sonnet-the-first-hybrid-reasoning-model-is-now-available-in-amazon-bedrock/ ↩︎
株式会社D2C d2c.co.jp のテックブログです。 D2Cは、NTTドコモと電通などの共同出資により設立されたデジタルマーケティング企業です。 ドコモの膨大なデータを活用した最適化を行える広告配信システムの開発をしています。
Discussion