Pythonを使った一元配置分散分析(ANOVA)で統計解析
はじめに
こんにちは、D2Cデータサイエンティストの郷原です。
データ分析を行う際に、aとbとcの平均値を比較してaが一番大きかったけど、これは他の二つと比べて有意な差があると言えるのだろうか?
こんな疑問を持ったことはないでしょうか?
上記のような疑問を統計的に検証することができるのが分散分析(ANOVA)です。
本記事では、1つの因子による平均値の差を分析する「一元配置分散分析」について、Pythonを使って試してみようと思います。
一元配置分散分析とは
一元配置分散分析(ANOVA, Analysis of Variance)は、複数のグループの平均値を比較し、それらの違いが偶然なのか、それとも統計的に意味があるのかを検証するための手法です。この手法を使えば、「ある要因が結果に影響を与えているかどうか」を分析することができます。
例えば、異なる肥料を使った場合の植物の成長を比較するとしましょう。このとき、「肥料の種類」が分析対象の要因(独立変数)となり、「植物の成長量」が結果(従属変数)になります。一元配置分散分析では、複数の肥料を使ったグループ間で成長量に差があるかどうかを確認するのです。
要するに、「1つの要因(独立変数)」が「結果(従属変数)」にどれだけ影響しているのかを統計的に評価する方法と考えるとわかりやすいでしょう。
使用するデータセット
カリフォルニア州の住宅市場に関するデータセットであり、回帰問題などでよく使用されるサンプルデータになります。
- サンプル数:20640
- カラム数:9
| カラム名 | 詳細 | 型 |
|---|---|---|
| MedInc | 地域の世帯の中央値収入(単位: 10,000ドル) | float64 |
| HouseAge | 地域内の住宅の築年数の中央値 | float64 |
| AveRooms | 世帯1軒あたりの部屋の平均数 | float64 |
| AveBedrms | 世帯1軒あたりの寝室の平均数 | float64 |
| Population | 地域の人口 | float64 |
| AveOccup | 世帯1軒あたりの平均居住者数 | float64 |
| Latitude | 地域の緯度 | float64 |
| Longitude | 地域の経度 | float64 |
| MedHouseVal | 地域内の住宅価格の中央値 | float64 |
仮説と分析方針
今回は人口が多い地域ほど住宅価格が高くなるのではないか?(人口多い=大都市=物価が高い?)
という仮説をもとに分析をしていこうと思います。
そのため、人口の多さを5分割し、
「Very Low, Low, Medium, High, Very High」というグループに分けて、人口の数によって、統計的に有意な差は生まれるのかを調べてみようと思います。
使用するライブラリ
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import fetch_california_housing
from scipy import stats
今回はscipyのstatsを用いて分散分析を行っていきます。
データの確認
data = fetch_california_housing(as_frame=True)
df = data.frame
dataには辞書型のBunch(特殊な型)としてデータを格納するために、as_frame=Trueを引数に設定します。
(FalseにするとNumpy配列の状態で返されるみたいです)
実際にdataを見てみるとわかりますが、Bunch形式では分析に使用できる状態ではないため、.frameと書くことによってDataFrameのみをとってくることができます。
試しに中身を見てみると
display(data)

上記のようなデータが格納されているみたいです。
Population(人口)ごとに5つのグループに分ける
df["PopulationGroup"] = pd.qcut(df["Population"], q=5, labels=["Very Low", "Low", "Medium", "High", "Very High"])
pd.qcutを使用すれば、q分割することができます。また、pd.cutと異なり、分位数の基づいて分割できるため、今回のような大きさ順に分けたい時などは使用すると便利だと思います。
基礎統計量を見てみる
print(df.groupby("PopulationGroup")["MedHouseVal"].describe())
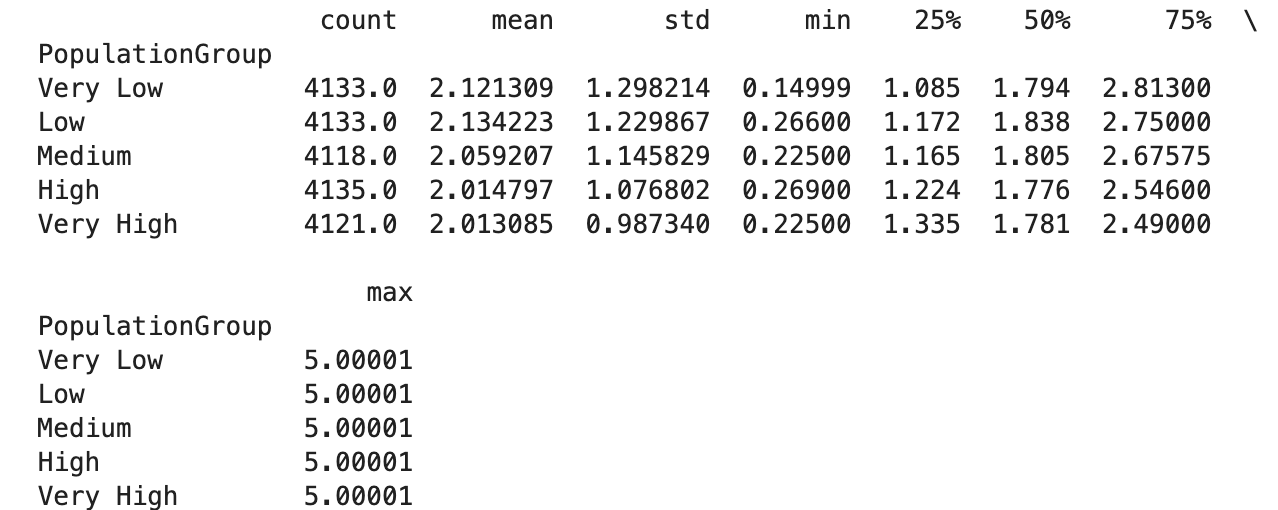
仮説とは逆の結果となり、人口が増えれば増えるほど住宅価格は低くなっていることがわかります。ただ、それと同じように分散も低くなっています。
そのため、平均値だけで人口と住宅価格の関係を説明するのは不適切であると言えます。
(ばらつき度合いが異なるため、外れ値などの影響を受けている可能性も考えられる)
データの散らばり度合いを箱ひげ図を用いて比較してみます。
plt.figure(figsize=(10, 6))
sns.boxplot(x="PopulationGroup", y="MedHouseVal", data=df, color = '#A0C4FF')
plt.show()
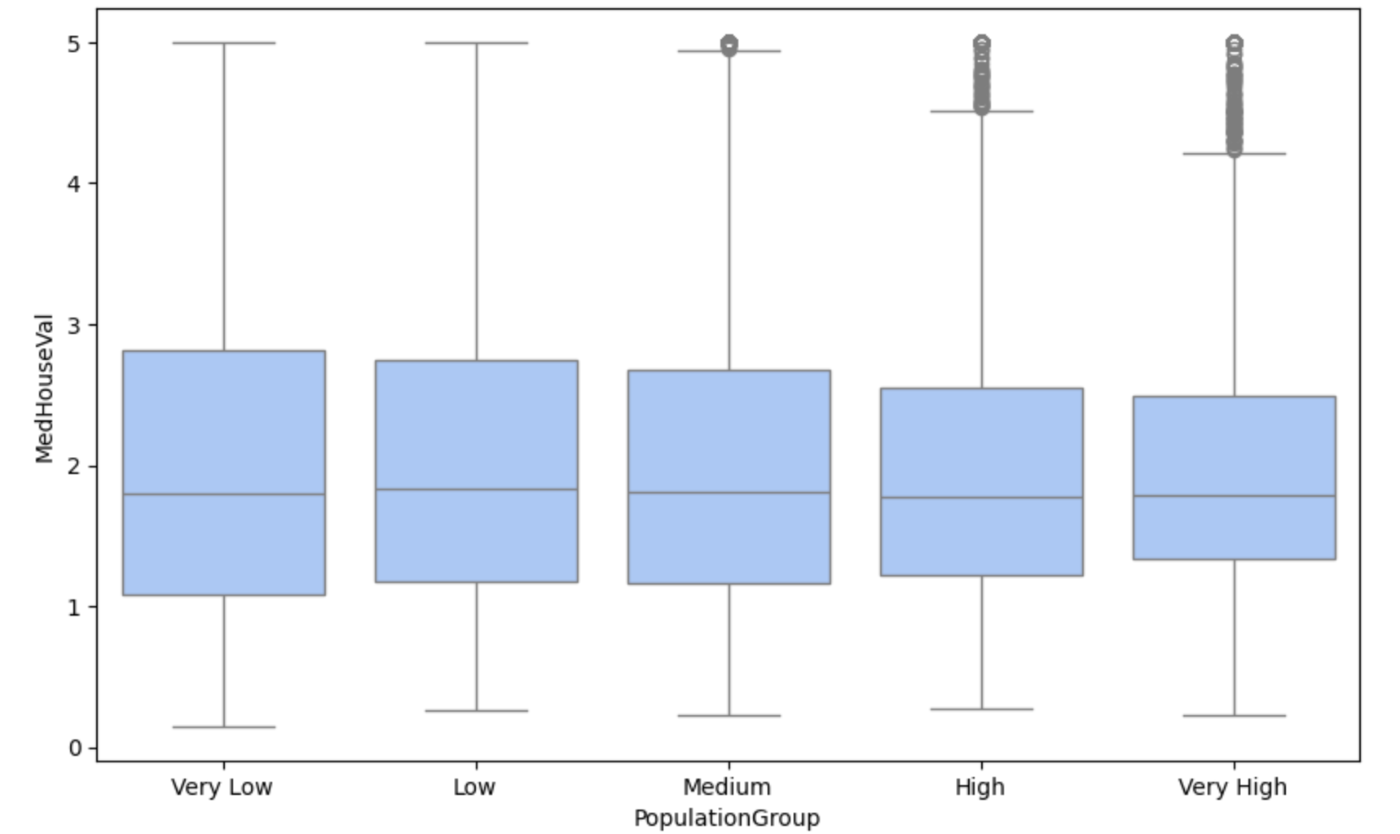
人口が多くなるにれ、四分位範囲が小さくなっていることがわかります。
分散分析(ANOVA)を行ってみる
今回はF統計量とp値という指標を使って人口数の違いによって、住宅価格に有意な差があるのかを調べていきます。
- F統計量:グループ間の分散とグループ内の分散の比率
- p値:帰無仮説が正しいと仮定した場合に、現在のデータが観測される確率
- 対立仮説:「人口が異なる5つのグループ間で、住宅価格の平均値には統計的な有意差がある」
- 帰無仮説:「人口が異なる5つのグループ間で、住宅価格の平均値には統計的な有意差がない」
今回はp値が0.05以下の時に帰無仮説を棄却するため、「人口によって住宅価格の平均値に有意な差があるグループもある」と言えます。
groups = [df.loc[df["PopulationGroup"] == group, "MedHouseVal"] for group in df["PopulationGroup"].cat.categories]
f_stat, p_value = f_oneway(*groups)
print(f"F-statistic: {f_stat}")
print(f"P-value: {p_value}")

まず、groupsという変数に、グループごとの値をリストに格納する処理を行っています。
f_onewayモジュールの引数には各グループのリストを与える必要があるため、*groupsにしています。
上記の結果より、p値は非常に小さく、F統計量も10以上(大きい)あるため、人口ごとの住宅価格の平均値には有意な差があると言えます。
まとめ
このように、分散分析のような統計的な手法を使うことによって平均値で大小比較するのだけでなく、その差が誤差の範囲なのかどうか(有意に差があるのか)を調べることができます。
詳しい計算方法や、分散分析については下記の記事が参考になるかと思うので参考にしてみてください。
最後までお読みいただきありがとうございました、この記事が皆さまのお役に立てれば幸いです。
参考記事
参考書籍
株式会社D2C d2c.co.jp のテックブログです。 D2Cは、NTTドコモと電通などの共同出資により設立されたデジタルマーケティング企業です。 ドコモの膨大なデータを活用した最適化を行える広告配信システムの開発をしています。
Discussion