VARモデルの実装に挑戦
はじめに
こんにちは、D2Cデータサイエンティストの郷原です。
本記事では、多変量時系列分析モデルの一種であるVARモデルについて、時系列分析初心者が自分なりの解釈と大まかなイメージを活用例をもとに紹介していきます。
もし、多変量での時系列分析を始める際に、本記事がお役に立てば幸いです。
VARモデルとは
VARモデルってなに?
VARモデルとは Vector Autoregression Model の略称であり、変数間の因果関係などを読み取ることができる多変量時系列分析手法です。
因果関係について詳しく
ここでの因果関係とは、変数Aを予測する際に変数Bが予測に有意な影響を与えてるかどうかを指します。そのため、実際に変数Aと変数Bに因果関係があるとは限りません。
例えば、とある商品の売上を予測する場合に、その日の最高気温のデータを使用したとします。ここでVARモデルにおける因果関係があったとしても、売上と最高気温に実際の因果関係があるとは言えません。
このようなVARモデルにおける因果のことをグレンジャー因果と呼び、下記方法で判定しています。
- 予測に使う変数Aと変数Bを用意
- 変数Bを予測に用いなかった場合と用いた場合の予測残差を比較
- 変数Bを予測に用いた時に予測残差が減少している場合、グレンジャー因果があるとみなす
VARモデルでは、グレンジャー因果がある場合のみ、その先の分析に用いることができます。
(グレンジャー因果がない=多変量にすると精度が落ちてしまう)
実際に使ってみる
使用データ
それでは実際にVARモデルを実装していきましょう。
本記事で使用しているデータはこちらのアメリカの小売店販売データになります。
こちらは過去にKaggleで行われていた Retail Data Analytics というコンペで使用されていたデータです。
今回は平均気温データ(Temperature)を使って、週の売上(Weekly_Sales)を予測していきます。
また、抽出条件はStore=11、Dept=1とします。
- Store : お店
- Dept : お店の中のとある部門
- Weekly_Sales : 週の売上
- Temperature : 週の平均気温
使用するデータをプロットしてみます。
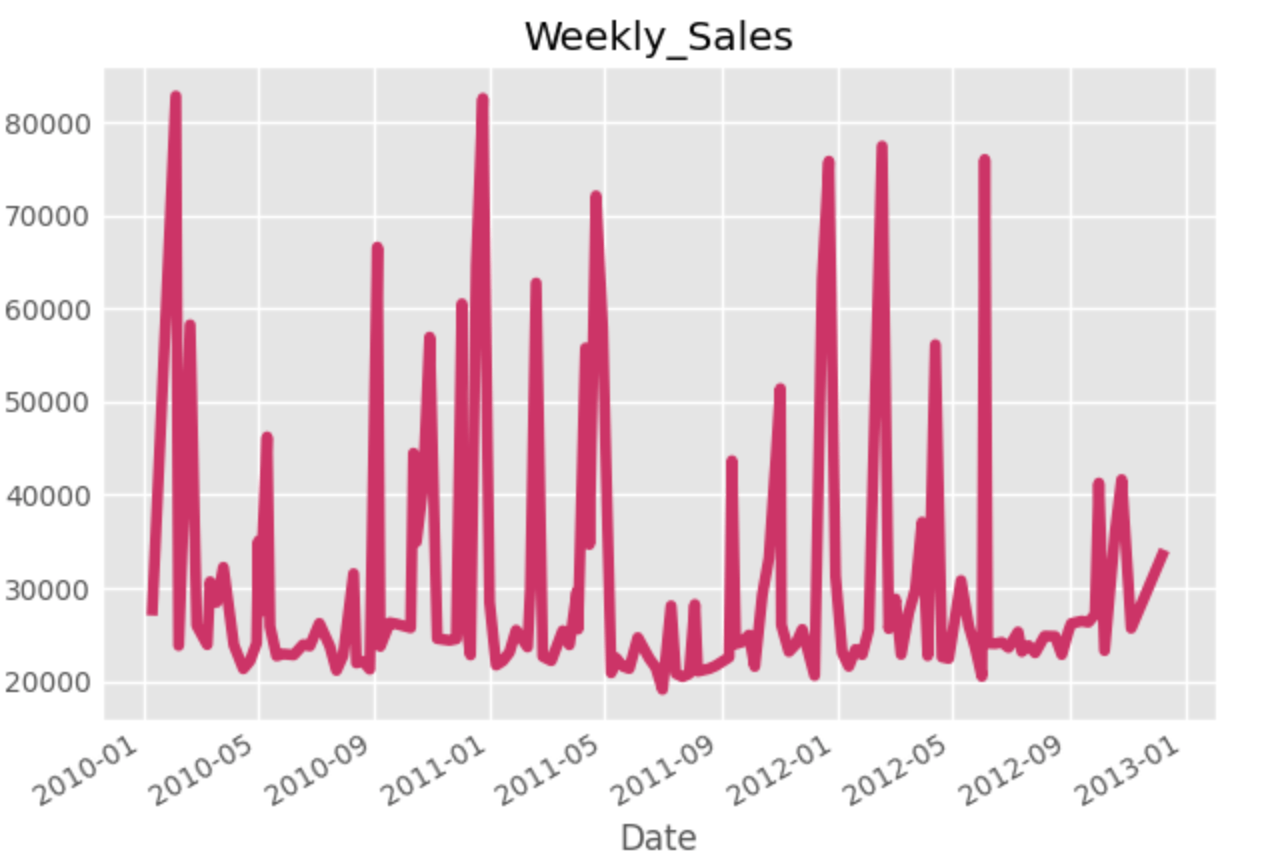
データは3年分くらいあり、分析に使用できるだけのデータ量はありそうな印象です。
グレンジャー因果の確認(0:Temperature,1:Weekly_Sales)
endog = df1[['Temperature','Weekly_Sales']].to_numpy()
model = VAR(endog)
model_result = model.fit(maxlags=11, ic='aic')
model_result.test_causality(causing=0, caused=1)

結果は0.047程度(0.05以下)なので、グレンジャー因果はあるといえそうです。
インパルス応答
インパルス応答とは、変数Aにある一定のショックを与えたときに、変数Bにどのような影響があるのかを可視化できるものです。
ここでは、平均気温が増加したときに、売上がどのように変動するのかを見ることができます。
実際に下記コードでプロットしてみます。
fig, ax = plt.subplots(figsize=(6, 4))
ax.plot(irf.orth_irfs[:, 0, 0], linestyle='-', marker='o')
plt.title('Temperature→Temperature')
plt.show()
fig, ax = plt.subplots(figsize=(6, 4))
ax.plot(irf.orth_irfs[:, 1, 0], linestyle='-', marker='o')
plt.title('Temperature→Weekly_Sales')
plt.show()

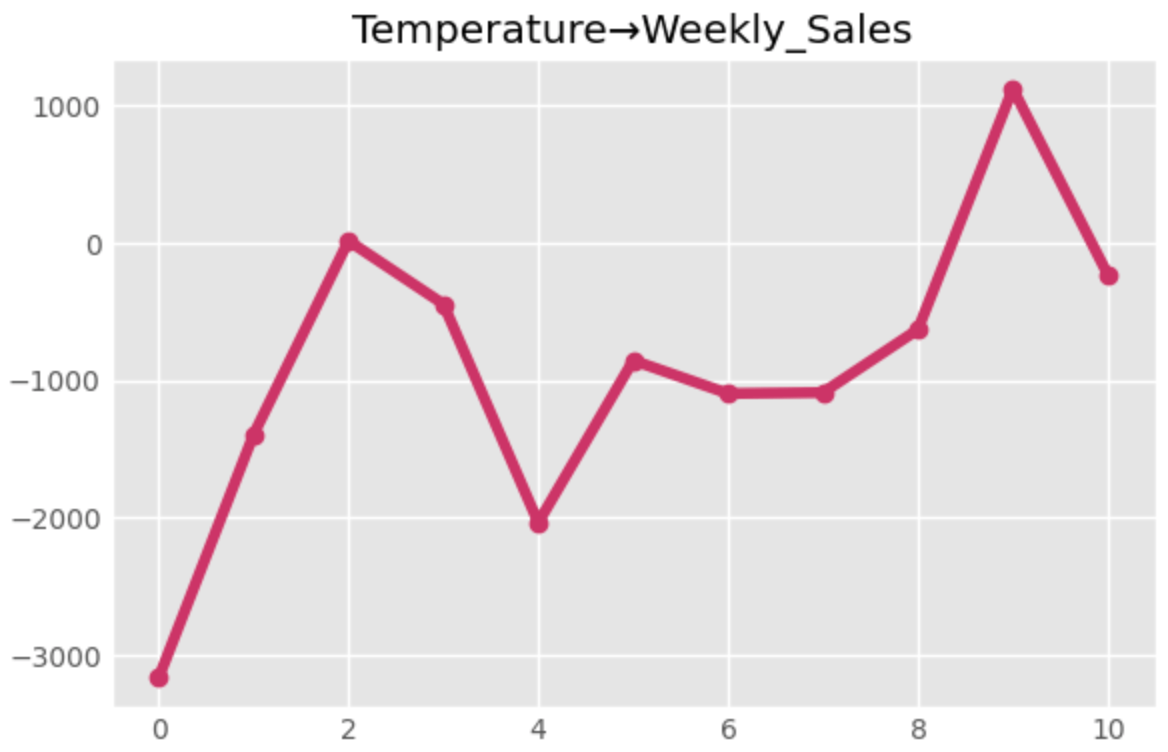
これら2つのグラフを見ると、平均気温にある一定のショックを与えた時に、売上が-3000になっていることがわかります。また、2週間後には売上は0あたりになっています。
この結果から、平均気温が上がると売上は下がり、2週間後にはほとんど影響がなくなっているように読み取れます。
分散分解(FEVD)
分散分解とは、予測に寄与する割合の変化を算出したものになります。
今回だと、売上の予測に平均気温データがどれくらい寄与しているかを知ることができます。
fevd_values = fevd_results.decomp
fevd=pd.DataFrame(fevd_values[1],columns=['Temperature','Weekly_Sales'])
fig, ax = plt.subplots(figsize=(6, 4))
ax.plot(fevd['Weekly_Sales'], label='Weekly_Sales', linestyle='-', marker='o',color='#3366CC')
ax.plot(fevd['Temperature'], label='Temperature', linestyle='-', marker='o',color='#CC3366')
ax.legend()
plt.title('FEVD_plot')
plt.show()
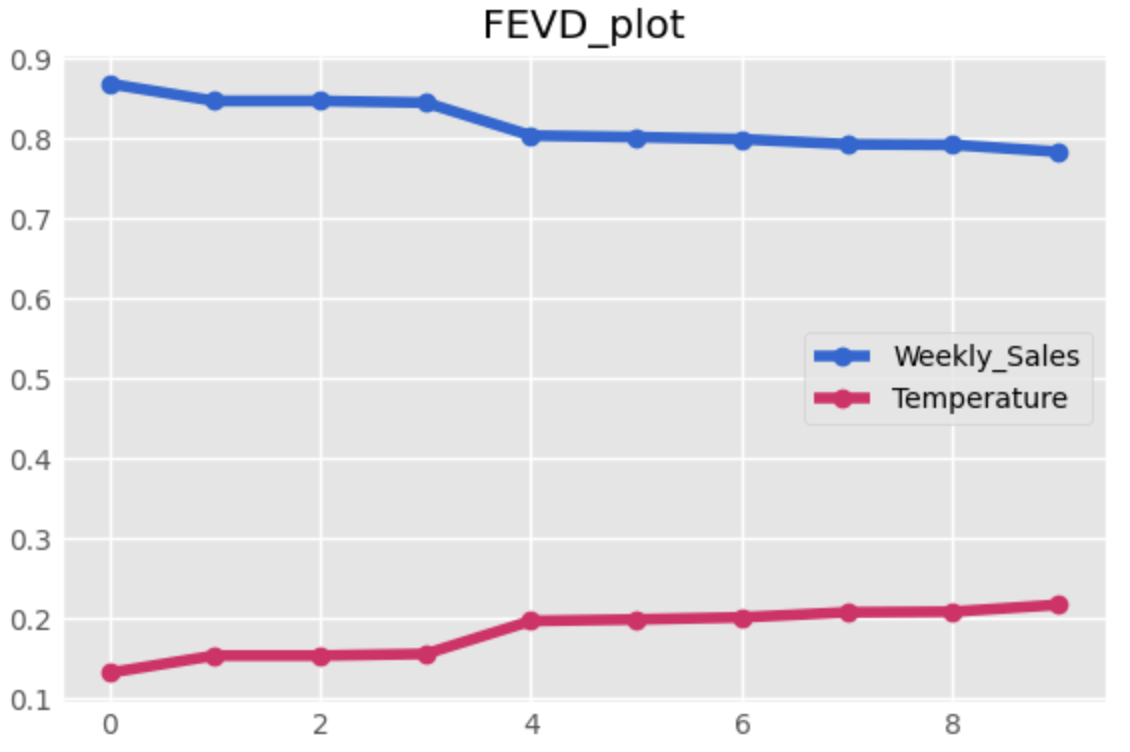
これを見ると4週間(約1ヶ月)後に平均気温の寄与率が少し上がっているようです。
また、平均気温データは1~2割ほど売上の予測の際に寄与していることがわかります。
予測結果
最後に、8週間分の予測結果の出力とプロットをしてみましょう。
predict = model_result.forecast(model_result.endog, steps=8)
predict = pd.DataFrame(predict,columns=['Temperature','Weekly_Sales'])
fig, ax = plt.subplots(figsize=(6, 4))
ax.plot(predict['Weekly_Sales'],linestyle='-', marker='o')
plt.title('Predict_plot')
plt.show()
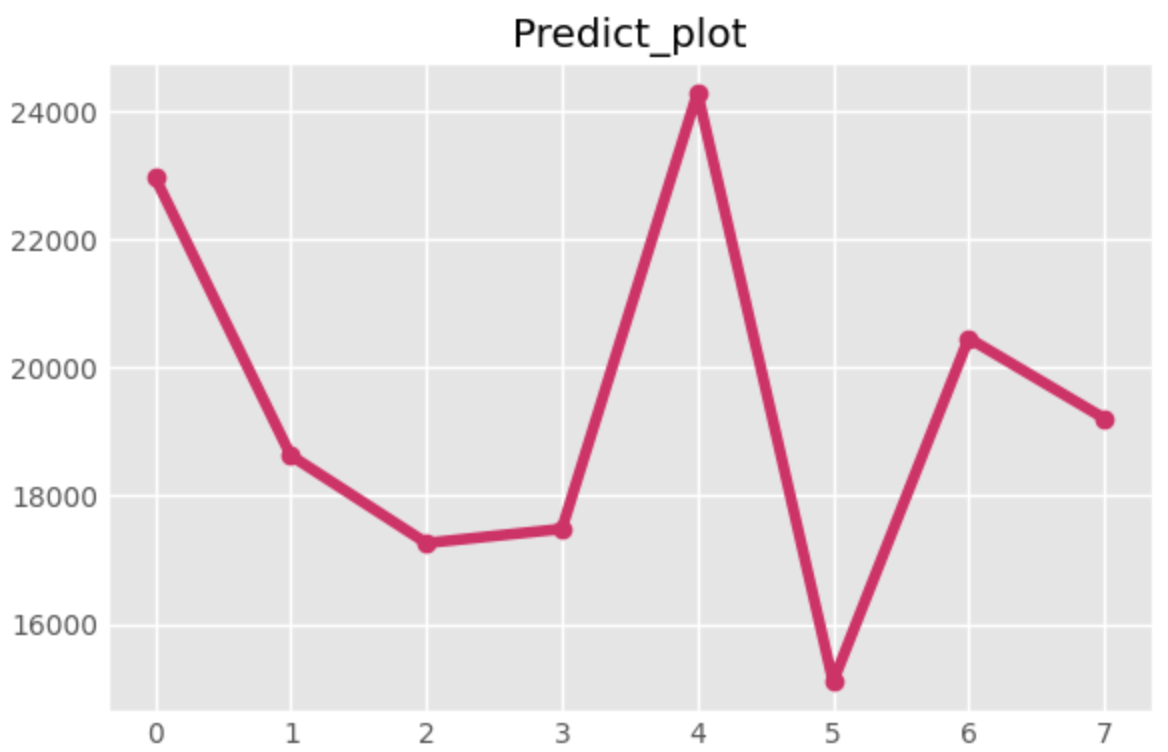
無事プロットができました。
今回は一通りの流れの説明なので、実際に精度を見たりしていませんが、検証用データなどを用意して精度を測ってみるとより良いモデルができると思うのでぜひ試してみてください。
モデリング時の工夫
ここからは、実際にモデリングをする際に工夫できる点をいくつか紹介していきます。
定常性の確認
定常性とは、平均や分散が常に一定であり、時間と共に変化しない状態のことを示しています。
VARモデルなどでは本来、定常性のあるデータを使用した方が良いとされています。
また、時系列データは季節性などによって、非定常データであることが多いです。ここでは非定常データを定常データに変換する手法の一つである、差分を取る方法を紹介します。
df1['Weekly_Sales'].diff().dropna().plot()
plt.title('Weekly_Sales_diff')
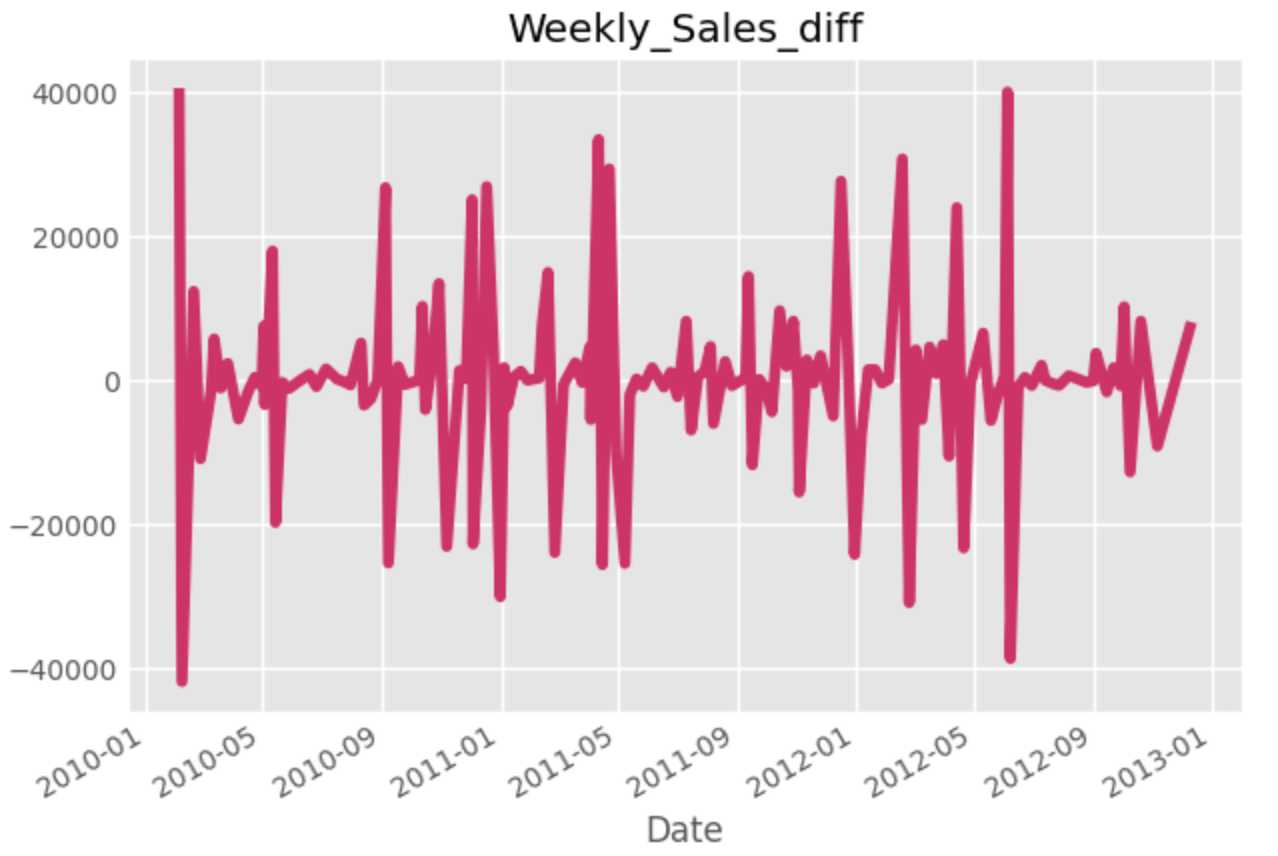
diff()を使う際は1行目がNaNになってしまうのでdropna()等で行ごと消してしまいましょう。
なんとなくx=0を中心に振動しているのが分かると思います。
また、ADF検定などを使えば、実際に定常かどうかの判断ができますが、今回は割愛いたします。
ハイパーパラメータ
VARモデルを実装する際に、こちら側で入力する必要があるパラメータは2つあります。
- ラグ次数(maxlags)
- 情報基準(ic)
これらを調べられる一番簡単な方法を今回はご紹介します。
print(model.select_order(20).summary())

するとこのように最適なラグを情報基準ごとに出力してくれます。
今回だと、aicのラグ次数が11の地点での数値が1番低いとわかります。
最後に
本記事では、多変量時系列分析の一種であるVARモデルの自分なりの解釈と大まかなイメージを活用例をもとに紹介させていただきました。
まだまだ時系列分析の全てを理解するのには時間がかかりそうですが、導入として知っておくと便利な情報を中心に記載してみました。これを機に時系列分析について興味を持っていただけたら幸いです。
最後までお読みいただき、ありがとうございました。
参考記事
参考文献
時系列分析と状態空間モデルの基礎: RとStanで学ぶ理論と実装(著 馬場真哉 プレアデス出版 2018年)
株式会社D2C d2c.co.jp のテックブログです。 D2Cは、NTTドコモと電通などの共同出資により設立されたデジタルマーケティング企業です。 ドコモの膨大なデータを活用した最適化を行える広告配信システムの開発をしています。
Discussion