AUCをちゃんと説明できないはずがない

正直なところ　ずっと自信がありませんでした　今日までは。(独白)

こんにちは、D2C^[1] データソリューション部のYと申します。
機械学習を学び始めたら精度指標として最初に出てくるであろうAUCは、ライブラリさえ使えば数行で扱えますが原理は意外と丁寧に解説されないことが多いのではないでしょうか。
あえてこの時代に、わざわざ、その値の意味や意義を精緻に理解して他人にわかりやすく説明できるようにすることを目標とし、自戒を込めて本稿を上梓します。

I.はじめに

(1)この記事の30秒サマリ

• 混同行列は、実データとモデルの予測結果を組み合わせ、機械学習モデルが直面する「射撃精度」と「撃ち漏らし回避性能」のトレードオフを評価するためのもの
• 検出したい事象を陽性、それ以外を陰性と呼ぶ時、
  • AUCは撃ち漏らし回避性能の評価を応用してスコア上位者からすくい上げた時の陽性者の件数に着目し、「陰性は陰性らしく低いスコアを、陽性は陽性らしく高いスコアをどの程度あてがえているのか」という予測スコアの順序性を指標化したもの
  • 陽性が著しく少ないと簡単にズルができるので、PR-AUCが有用。これは、同様に射撃精度向上と撃ち漏らしの両方の観点に注目し、モデルが両者をトレードオフながらもどれだけまんべんなく最大化できているかをスコア化したものである

(2)なぜAUCを理解するのが難しいのか

個人的経験を踏まえですが、AUCの理解を阻害する要因は2つあると思われます：

• ①5割: 混同行列、及びそこから算出される各指標(アルファベットのオンパレード)が導入動機なしにいきなり出てきてしまい、意味的整理がきちんとされないから
• ②4割：混同行列からROC曲線やAUCに至る動機、および導出の過程が十分に説明されないことが多いから

結局は説明不足が9割だよねという話なので、これに対し、本稿では①②の解説を図ったほか、あわせて有用なPR-AUCについても紹介します。
(他、1割が英語翻訳のされ方によるものではないかという話を述べます)

II.AUCを順を追って理解する

(1)混同行列：「射撃精度」と「撃ち漏らし回避」

機械学習の性能を考える上で、まず混同行列(confusion matrix: cm)なるものを導入します。
これは、正解のデータのクラス件数と予測されたクラス件数を縦横に配置することで、「現実にはこうなのだがそれを機械学習はどう捉えたのか？」という性能を分かりやすく可視化する道具です。^[2]

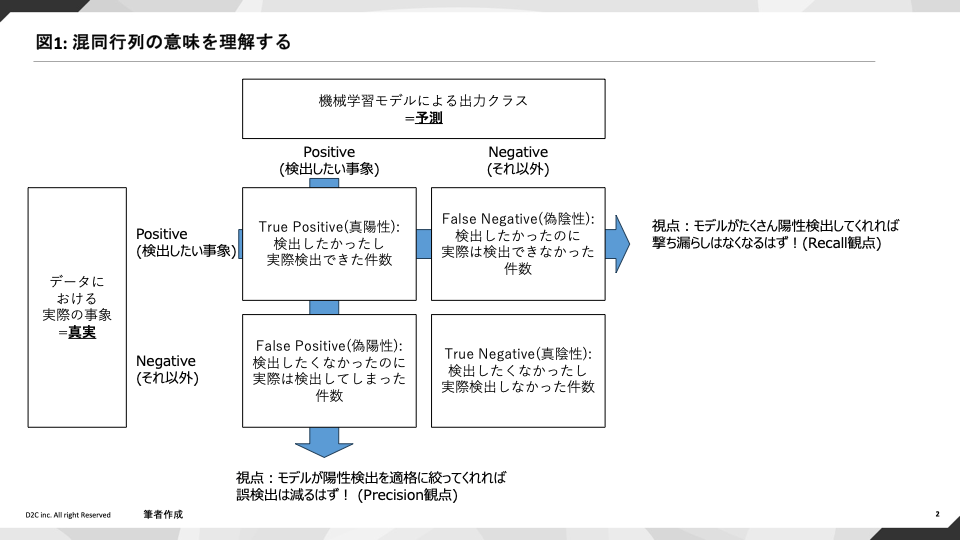
まず全般的な見方として、どのような目的のモデルであれTrue Positive(TP: 陽性検出したかったし実際に検出できた=本当に陽性だった)とTrue Negative(TN: 検出したくなかったし実際陽性検出しなかった=本当に陰性だった)は望ましいことであり、あらゆる意味でこのモデルの推論は「正解」といえるでしょう。
これに対応した評価指標として、後述のAccuracy(「正解」率)というものがあります。

次に詳細を評価するために、ここからモデルを特定の利用目的に沿って深掘りしようと思った際に、機械学習のトレードオフとして、的中精度の向上と予測し漏らしの回避という2点を選択せねばねばならないという事実を理解しておくことが肝要です。
射的でたとえますと、当てたい的(=検出したい事象)があった際にもしなるべく「正確」に的中させようと思えば確実に射抜ける的だけを絞って撃つわけであり、それは射抜けそうにないが存在する的をいくらか見捨てることになってしまいます。
一方で、的に対する撃ち漏らしを回避したいのならばひたすらに弾を打っていれば良いわけですが、弾のムダ打ちが避けられないということです。
ここでいう射撃の精度にはPrecision、撃ち漏らしの回避性能(機会損失の回避と言っても良い)にはRecallという名前がついています。^[3]
重要なのはTP、FPなどのアルファベットの並びそのものではなく、これらの計算に対する意味的な理解であるということに留意されたいです。

(a)Accuracy / 「正解」率

前掲の通りAccuracyは全般的な見方ですから、混同行列において「正しい分類」、すなわちTPとTNが全体においてどれだけを占めるかという点で表現されます。

Accuracy = (TP + TN) / (TP + FN + FN + TN)
≒ 狭義の正しい分類 / すべてのデータ件数

(b)Precision / 適合率： 射撃精度

Precisionの利用目的は「なるべく無駄打ちを減らすために、陽性だと自信をもって予測できる的ののみ正確に射撃するようなモデルを評価すること」ですので、陽性予測者のうち実際どれだけが陽性者だったのかで評価指標をつくることが妥当でしょう。故に、

Precision(適合率) = TP / (TP + FP)
≒ 正しく陽性予測した件数 / ムダ撃ちを含め、陽性だと予測した件数

と定義されます。当然、大きい方が望ましい値ですね。

(c)Recall / 再現率 / TPR：撃ち漏らし回避

同様に、Recallは「なるべく撃ち漏らしを少なくし、陽性者を漏れなく検知するモデルを評価すること」を目的とした指標ですから、実際の陽性者のうちどれだけをモデルが陽性だと予測したか、拾えたかを指標として考えれば良いでしょう。故に、

Recall(再現率) = TP / (TP + FN)
= 陽性だと予測し、当たった数 / 実際の陽性者の件数

と定義することができます。Precision同様に大きい方が望ましい値です。

Recallは、陽性だと正しく予測できた件数(TP)を実データの陽性件数(TP+FN)で割ることから、
全陽性者に占める正陽性予測件数の割合ということでTrue Positive Ratio, TPRとも呼ばれます。

なお、後述するROC曲線においてRecallとセットで評価されるのが、FPR False Positive Ratioというものです。
これは混同行列でRecallより一つ下の行で同様の計算をしたものであり、実際は陰性であるのに誤って陽性と検知してしまった割合のことを指し、こちらは小さい方が望ましい値です。

(2)現実問題にあてはめて考える

掲出の指標群を、過去のアクセスデータからECサイトでの商品購入を予測するモデルにあてがって考えてみましょう(Positive = 購入)。
ここで再現率(Recall)を増やすことは機会損失の可能性を最小化するのに有用で、例えばマスマーケティングとしてクーポンを配布する施策での配布先最適化モデルとしての妥当性を評価できるでしょう。
一方で、適合率(Precision)を増やすことはお客様が購入をしそうだという予測の確度を最大化させられるため、ロイヤリティの高そうなお客様に絞ってキャンペーン施策を打ちたい場合に適した指標だと言えます。

(3)おまけ：指標と翻訳

データサイエンス界隈ではaccuracyを「正解率」、この手の指標を束ねて「精度」評価指標と呼ぶことが一般的かと思われますが、我々日本語話者の翻訳慣習に従えばaccuracyこそ「精度」と訳すのが妥当ではないでしょうか。

評価指標という意味でmetricsという単語が使用された場合、英語では概ねperformanceにかかることが一般的であると思われ^[4][5]、最適化する対象はモデルのperformanceであるわけですから、performance metricsには「能率評価」ぐらいの翻訳が妥当なのではないでしょうか。
その意味で、強調のために「正解率」や「精度」を指す場合にはすべて括弧を付したいのですが、かえって読みづらくなると思われるので以降は割愛します。

(4)なぜこれだけでは不十分なのか：ROC曲線とAUCのモチベーション

ここまでで機械学習におけるトレードオフが理解でき、混同行列を用いて各指標を定量評価できるようになりましたので、これで評価指標としてはもはや十分ではないのでしょうか？
これで終わってしまうと、実務的なレベルでは2点問題が生じます。^[6]

(a)閾値の問題

まず、前掲の混同行列は評価時に予測モデルが0/1のクラス出力を行っていなければならず(当たり前)、連続値の出力に対して適用する際には閾値を決めなければならないという制約があります。

筆者の実務的感覚ですが、検出したい事象を予測する機械学習モデルを作る際に、いきなり0/1のクラス分類を行うことは少ないのではないでしょうか。
前述のユーザー購入予測モデルでいえば、むしろ0以上1以下の連続値として購入確率を予測するモデルを作成し、その予測スコアの高低をもって施策適用するのが一般的なはずです。

この閾値の設定をどうすればモデルを客観的に評価できるのか、という点が問題としてあがります。

(b)すくい上げと順序性の問題

もう一点は、予測モデルの出力したスコアの順序的な確からしさをどう評価すればよいのかという問題です。
前章で「予測スコアの高低をもって施策適用するのが一般的」と書きましたが、これは具体的には購入予測スコアの上位N万人に絞ったお客様に特定のキャンペーン施策をあてがう、あるいはNをゆるやかに設定してまんべんなくクーポンを配信するなどのユースケースにあたります。
ここでモデルの良いパフォーマンスとして問われているのは「スコア上位者からすくい上げた時に、どれだけのタイトな / ゆるやかなすくい上げ方をしても適切に陽性者を検出できているか」であり、言い換えると「低い予測スコアが付されたデータ群には陽性の発生確率が低く、またスコアが高ければ陽性の発生確率が高い状態をどれだけ担保できているか」というスコアの順序性の問題であるわけです。

RecallやPrecisionはあくまでモデルの出力結果を静的に眺めた評価であり、そうしたスコアの内実を動的に見るような評価は行えないわけです。

これら2つを解決するのが、ROC曲線(Receiver Operating Characteristic curve)^[7]およびそこから算出されるAUC(Area Under the Curve)なのです。

(5)ROC曲線とAUC

ROC曲線は前掲の問題点を鑑み、「それならば閾値を少しずつずらして連続値を扱い、予測スコアのスコア上位者から拾い上げていった時の様子を評価すればいいじゃないか！」 という視点を取ります。

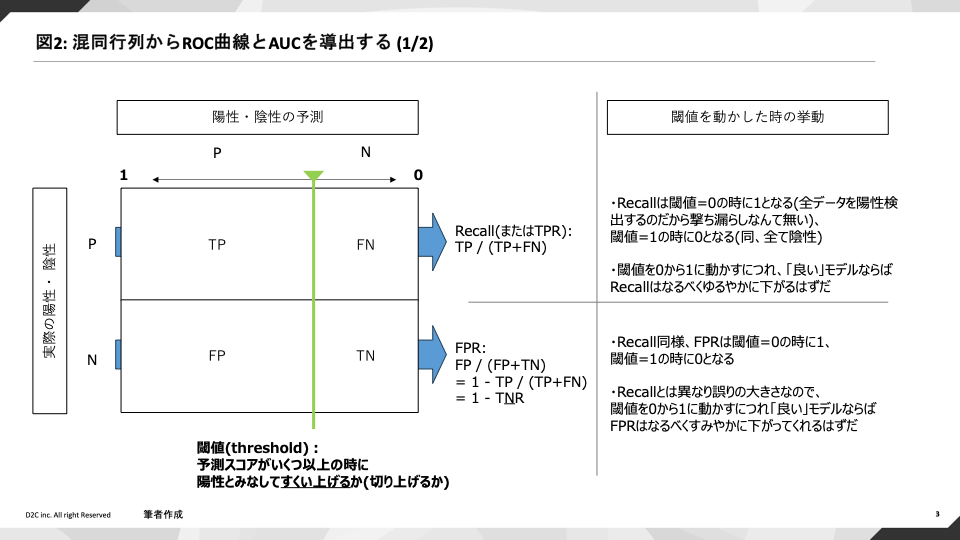
ROC曲線は連続値である予測スコアの閾値を少しずつずらすため、混同行列に対してその「しきいの線」(予測としてのPositive | Negative)を少しずつずらしていくような見方をし、そこに置いて指標がどのような値を取るのかを考えます。
その際、分かりやすく影響を受けるのは(TP+FNに占めるTPの割合を評価している)Recallと、同様の計算を陰性を誤って陽性検出観点で行っているFPRですから、これらを対置して考えます。

まず閾値を0に設定した場合、これはどんなスコアをモデルが出力しても陽性予測とみなすということですから、Recall(撃ち漏らし回避の度合い)は当然1であり、
本当に陰性の正しい検知がされないわけですからFPRも1を取ります。
同様に、閾値が1の場合は陽性検出が実質的に全くされないわけですから、Recall・FPRともに0となります。

スコア上位者からのすくい上げの観点で我々が「良いモデル」に期待する動きとしては、どのような閾値をとってもなるべくRecallが高い状態を維持していることであり、
対置されるFPRは陽性誤検出の比率ですからなるべく低くあって欲しいというものでしょう(図2参照)。

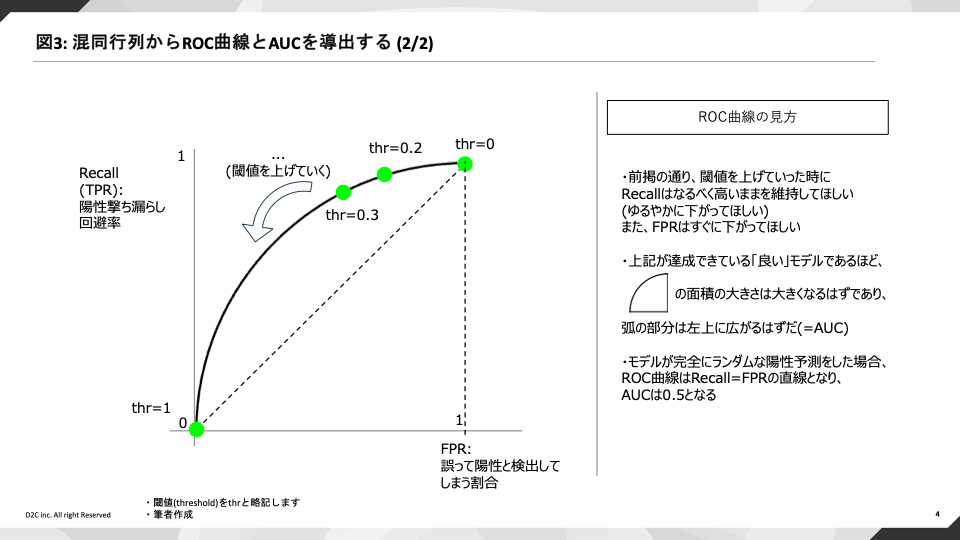
閾値を増減させた時のRecallとFPRの値を二次元平面にことでモデルに描画すると、図3のような孤が描かれます。^[8]
これがROC曲線であり、孤が描いた右下側の面積の大きさをAUCと呼びます。
RecallとFPRが同じ割合で減っていく場合(図中央の点線に相当)と比べ、Recall性能が良いものである(閾値を上げて言ってもRecall性能がなるべく下がらないでいてくれる)ほど曲線は左上に伸びていき、AUCも1に近似されます。

III.AUCの問題点：不均衡データ

AUCでスコアの順序性も評価できるようになったのだからもう十分そうなものですが、
AUCは陽性のデータ数が少ない不均衡データに対して過度に高く算出されてしまうという弱点があります。

例えば1万レコードのうち陽性者がわずか数件しか無いデータを予測したとします。
この場合、Recallはその数件だけを陽性と撃ち漏らさなければ良いわけですから高いRecallを担保するのが比較的容易にでき、ROC曲線も容易に左上に引きつってしまうことになります。

そこに待ったをかけるのがPR曲線です。

IV.待ったをかけるPR曲線とPR-AUC

Precision-Recall曲線はその名の通りPrecisionとRecallのトレードオフの関係を予測スコアの閾値を増減させて描画した曲線のことです。
理解に必要なパーツは既に出てきたもののみです。

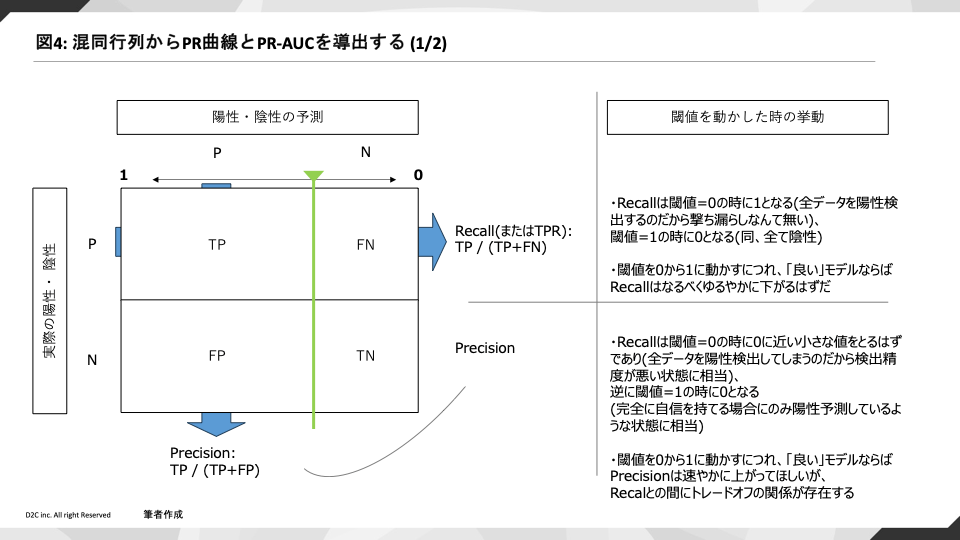
不均衡データに対してRecallが過度に高いことでモデル評価が引っ張られてしまう状況を防ぐために、
Precisionという観点を併せて評価します。
スコア上位者を陽性とみなしてすくい上げる際に、撃ち漏らしは減らしつつ一方で適格に陽性者だけを検出するという、その相反する期待をモデルに課し、能率を評価するのです。

ROC曲線にならって描画された面積の大きさをPR-AUCと称し、この値が1に近いほど「良い」モデルと判断できるわけです。

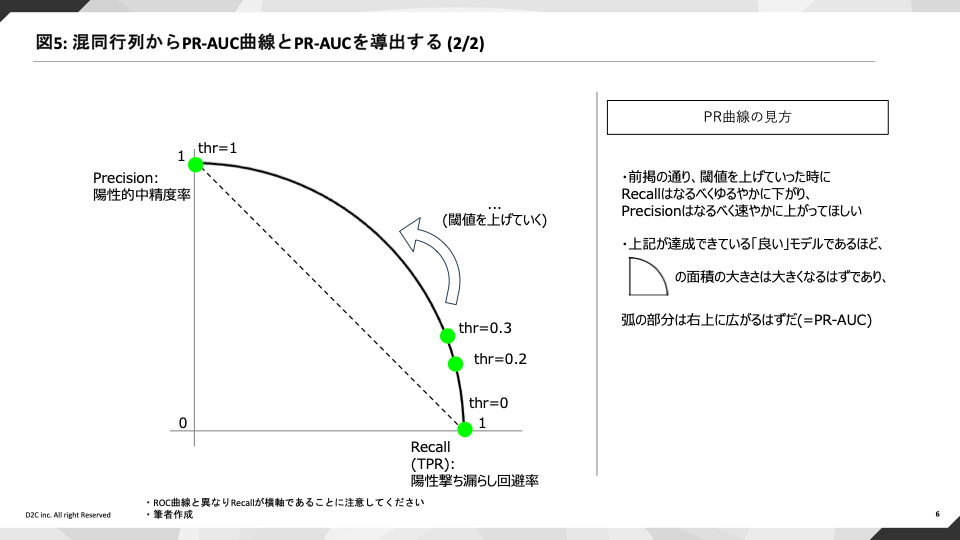
実務的にPR-AUCで高いスコアを獲得することはかなり^[9]難しく、モデルの妥当性を厳しく評価するのに優れた指標です。
初手としてAUCを評価し、PR-AUCを併せて用いるというユースケースが多いように見受けられます。

V.終わりに

基礎的な内容で記事を書くのは無知を晒す恐ろしさがありましたが、勇気を持って出稿しました。
本稿が誰かの役に立ちましたら望外の喜びです。
弊社テックブログでは技術話題について日々更新しておりますのでぜひ他の記事もご覧くださいませ！

採用情報

D2Cグループではデータサイエンティスト、エンジニアの方々を募集しています。
ブログを読んでD2Cで働いてみたいと思った方、D2Cの業務に興味をもってくださった方がいらっしゃいましたら是非ご応募ください。

▼ D2Cグループ採用サイトはこちら
https://recruit.d2c.co.jp/

▼ D2C問い合わせフォームはこちら
https://www.d2c.co.jp/inquiryform/

参考

• 【評価指標】ROC 曲線と AUC についてわかりやすく解説してみた　グラフィカルで優れた説明として参考にしました
• [第3版]Python機械学習プログラミング 達人データサイエンティストによる理論と実践 / Sebastian Raschka (著), Vahid Mirjalili (著), 福島真太朗 (監修), 株式会社クイープ (翻訳)
  (PP.186-187に掲載されている解説、及び疾病予測モデルを用いた評価指標解釈の明瞭な例示を、本稿「現実問題に即して考える」章で参考にしました)

脚注

1. 弊社の社名です。direct-to-commerceの略ではありません。

2. 実データの陽性・陰性を横軸、予測出力を縦軸に取った混同行列もあるようですが、以降の説明のしやすさを鑑みて横軸に予測出力を表す構図を採用しました。 これが本当のconfusion...

3. ほか、PrecisionとRecallの調和平均を取ったF1 scoreというものもありますが、後述する閾値を設定しないと評価に用いることができないという他指標と同様の使いづらさを抱えており、AUCやPR-AUCを用いればその使いづらさをカバーできることから、紹介を割愛しました。

4. 例1：Stanford大学での講座にて、"(...)there are evaluation metrics that encapsulate (中略) performance."と表現されています。

5. 例2:Data Science Performance Metrics for Everyone 記事タイトルが物語っています。
   もちろんすべての英語話者がこれらのように表現するわけではないでしょうが、それでもperformanceのmetricsという言い回しが一定の一般性を持っているとは解釈できるのではないでしょうか。

6. 学術的な意味での問題意識がどうだったのかという点では本稿は調査不十分です。いつか追って追記したいと思います

7. ROCのCはcurveではなくcharacteristicのことなので、Kiyomizudera Templeのような誤用にはあたらないです。

8. 一般的には閾値を1から下げていき、ROC曲線を左下から右上へ描くものとして説明されます。しかし、AUCが前掲の「スコア上位者からのすくい上げ」観点での評価指標であり、閾値上昇によりRecall(撃ち漏らし回避性能)が低下していくさまを述べたほうが理解が容易にすすむと考え、この手順で説明しました。

9. 実務家諸氏のコメントを待ちたいです。サンプルデータを使ってよく表現される「PR-AUCが0.95です」のような素晴らしい状況は、個人的には現実の分析命題ではまずお目にかかれないだろうなと思います。