SPARF: 少ない画像、曖昧なカメラパラメータでも3次元シーンを学習可能なNeRFの紹介

はじめに

初めましてD2Cデータサイエンティストの吉井です。

普段はリサーチ関係の業務に携わっておりますが、データ分析で得られた知見を社外の研究会等で発表したり、社内向けに勉強会を開いたりなど、最新の研究に追いつけるよう日々努めております。

今回の寄稿の機会を受けて、最新のトレンドであるNeRFに関連する記事を執筆することに決めました。

背景・動機

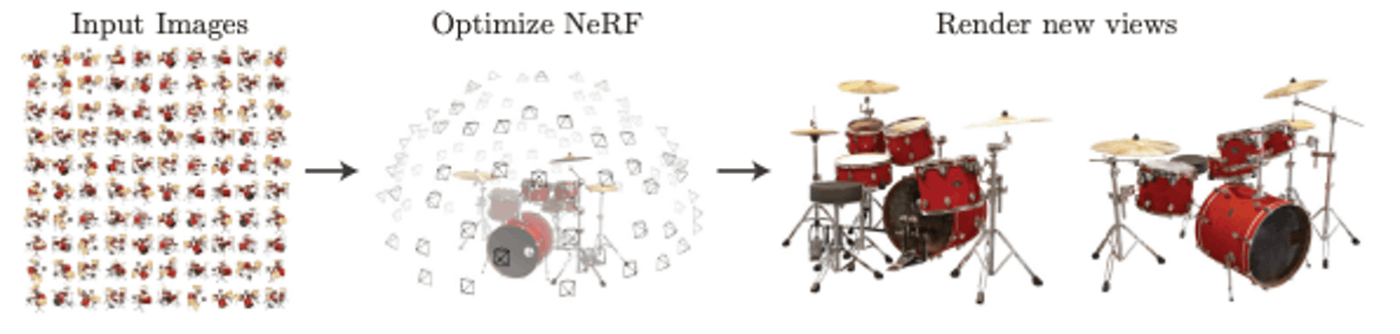
NeRF(Ben Mildenhall et al. 2020)は複数の視点画像から新たな視点画像を生成する技術です。図1のドラムを囲うように撮影したカメラ画像とカメラパラメータ(カメラの位置座標や姿勢等)から、Radiance Fieldと呼ばれる「場」のデータを学習します。このRadiance Fieldを使って、新しい視点からの写真を生成することができるのです。

図１. NeRFの概略図。ある３次元のシーンを複数の視点から撮影した画像を学習し新たな視点の画像を生成する技術 (出典:https://arxiv.org/pdf/2003.08934.pdf)

このとき生成する視点を連続的に動かすことで立体的にシーンを再現することができ、ダイナミックな映像を生み出せることから、すでに様々な企業で広告への活用がなされています。また空間把握の技術などへの応用も研究されていて非常に広い分野で注目されている技術です。

一方で、NeRFには高密度な入力画像とそれらの正確なカメラポーズが必要という欠点があります。大掛かりな装置を組めば複数視点・正確なカメラパラメータを持つ画像群を用意することは容易でしょうが、できることならスマホ程度のサイズ感で撮影したいものです。これまでの研究ではカメラポーズがわかってる疎な画像群からシーンを学習したり、カメラポーズが不正確で密な画像群からシーンを学習したりする手法が研究されてきましたが両者をいっぺんに解決する研究はありませんでした。

今回紹介するSPARFはこのNeRFが抱える問題点を同時に解決した手法で、カメラパラメータが不正確な疎な画像群(3枚程度)からシーンを学習することが可能です。この手法はCVPR2023に採択された論文でhighlightに選ばれたことから日本語圏のTwitter界隈でも密かな話題となっていました。

本記事は実のところ8月に公開する予定の記事だったのですが、私が体調を崩してしまい記事の執筆が間に合わなかったこともあり10月の公開となっています。本来ならば速報的な意味合いでこの記事を発表したかったのですが、9月末現在で日本語の解説記事は(私が調べた限り)出ていないようなので興味がある人の参考になれば良いなと思っております。

以下ではSPARFの具体的な手法を紹介する前に、簡単にNeRFの手法について紹介します。NeRFの紹介記事は日本語で詳しく紹介されている記事がたくさんあるため、簡単な図と式でイメージを伝えられるように紹介いたします。
また、SPARFの著者がgithubでコードを公開しています。この記事でもオリジナルのシーンを生成するところまでお見せしたかったのですが、コードではPublicデータの追試までしか実装されておらず、オリジナルデータでのシーン生成には一手間かかりそうだったため、今回の記事公開までには準備することができませんでした。再現が出来次第この記事(もしくは次回の記事で)の更新を予定しています**。

NeRF

まずは、NeRFの手法について紹介します。
解説にあたって図を使用しますが、本来NeRFが３次元のものを様々な角度から撮影した２次元の情報から復元するのに対して、本記事では２次元のものを１次元に射映した情報から復元するように捉えて紹介しています。
また、NeRFは画像座標、カメラ座標、世界座標の座標変換を多用する技術なのですが、本記事ではそれらの詳細な解説は行わずすべてカメラパラメータで変換可能なものとして扱っています。詳細な実装はそれぞれ公式の論文やgithubからご確認ください。

Radiance Field

まず、Radiance Fieldと呼ばれる「場」について解説します。
Radiance Fieldは空間中の任意の点が色(放射輝度)と密度の情報を持つ「場」のことで、各点は見る角度に依存して異なる色の放射をします。
３次元の立体を点群で表現するアイディアと同じで「もの」があれば密度が高く見る角度によって異なる色の情報をもち、「もの」がなければ真空で密度が0となり光を放射しません。煙やガラスのような後ろが透けて見えたり、同じ点でも角度によって反射で明るさが異なるものも表現できるのがRadiance Fieldの利点です。

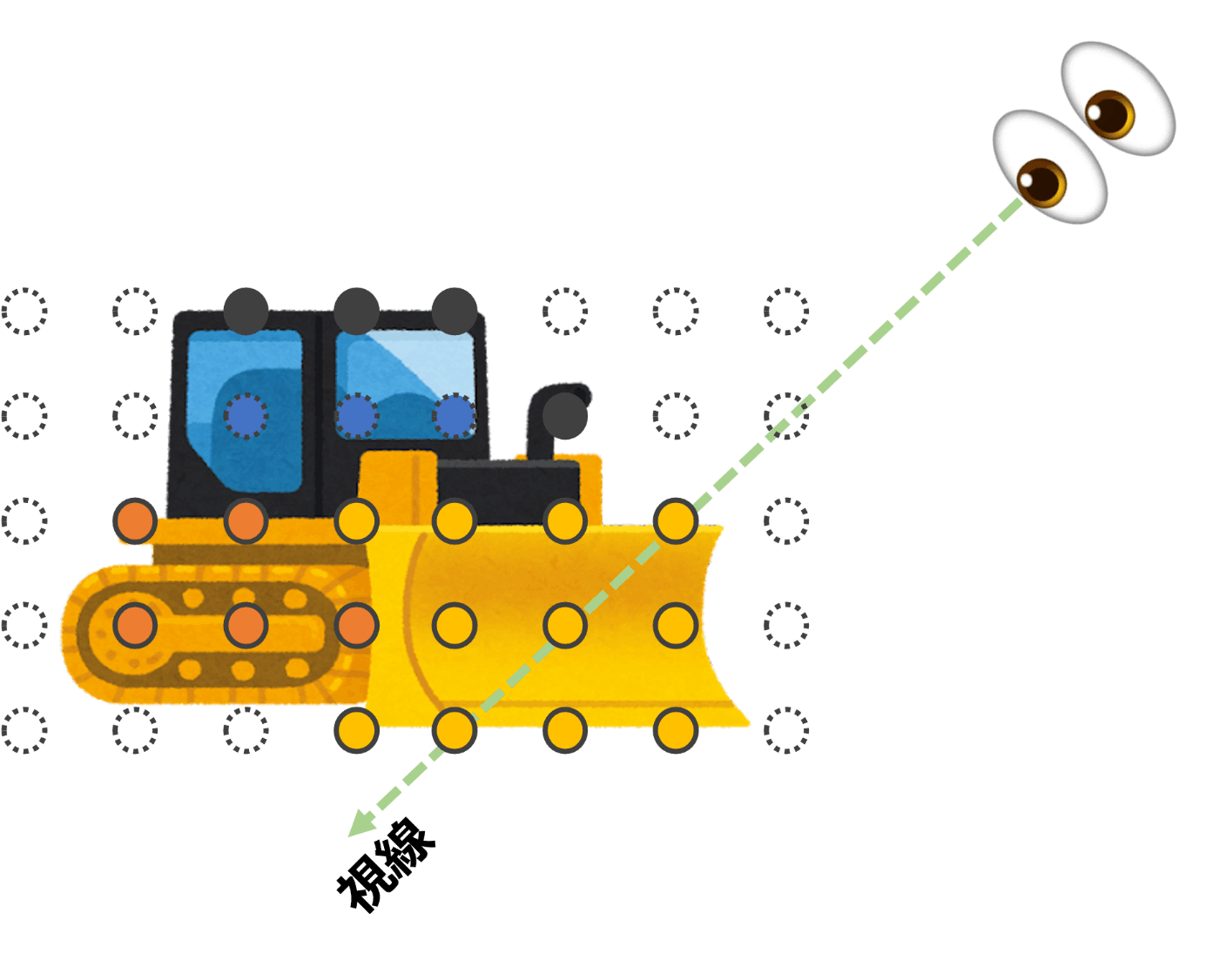
図2.1. Radiance Fieldのイメージ図。　Radiance Field中の任意の点は色と密度の情報を持っていて、色は見る角度によって変化します。図では各点が色を持ち、縁の線が実践なら不透明、点線なら透明を意味しています。

このRadiance FieldはNeural Netによって学習されます。このときNeural Netは空間上の座標$\bm{x}$とそれを観測する方向$\bm{d}$を入力することでその点の放射輝度$\bm{c}$と密度$\sigma$を出力する関数となっています。

Neural NetでRadiance Fieldを表現することからNeRFという名前が採用されているようです。

Volume Rendering

Volume Renderingは、Radiance Fieldをある方向から観測したときに得られる輝度を計算するプロセスのことです。
ある点から観測者に向かって放射される光は密度($\sigma$)と色(c)の積で決まります。また放射された光は観測者に到達するまでの空間で減衰し、それは観測者までに通過する点の密度の和から計算できます。

$$C({\bf{r, d}})=\int_{t_{n}}^{t_{f}} T(t) \cdot \sigma({\bf{r}}(t)) \cdot c({\bf{r}}(t), {\bf{d}}) dt$$

$$T(t) = \exp\left(-\int_{t_{n}}^{t} \sigma({\bf{r}}(s)) \right) ds$$

図2.2. Volume Renderingのイメージ図。視線方向上の各点から放射された光はスクリーンに到達するまでに前方の空間で減衰します。それらの重ね合わせた放射強度がピクセル上の輝度となります。スクリーン上のピクセルを走査することで画像を生成できます。

Radiance Fieldをある位置$\bf{r}$から観測した画像を生成するとします。画像内のピクセルを選ぶと視線方向$\bf{d}$が決まり輝度$C({\bf{r, d}})$を見積もることができます。このとき視線を少しずつ走査させることで画像を生成することができます。

model、学習方法

Radiance Fieldを学習するモデルは図2.3のようなMLPを重ね合わせた構造をしています。大まかに二段構成になっていて座標$\bm{x}$を入力して密度$\sigma$を出力する階層と、その後さらに視線方向$\bm{d}$を入力して色情報$\bm{c}$を出力する階層となっています。

図2.3. NeRFのモデル。(出典:https://arxiv.org/pdf/2003.08934.pdf)

Positional Encoding

モデルの図を見ると座標情報$\bm{x}$をモデルに入力する前に関数$\gamma(\cdot)$が適応されていることがわかります。これはPositional Encodingと呼ばれる関数で、座標に高速で振動する成分を付与する効果があります。

$$\gamma(p) = \left(\sin(2^{0}\pi p), \cos(2^{0}\pi p),\cdots,\sin(2^{L-1}\pi p), \cos(2^{L-1}\pi p)\right)$$

これはNeural Netで画像を生成する際に高周波成分を学習することが困難なためです。つまり連続的な入力では論文中のレゴブロックのような微細な構造を生成することができないため、あらかじめ高周波成分を持つ関数に通したものも入力に使ってしまおうというアイディアです。論文中では位置情報については$L=20$を採用していて3次元の入力$\bf{x}$の各成分に適応して60次元に、方向成分については$L=12$を採用して2次元の入力$\bf{d}$を24次元にしています。

図2.4. NeRFの論文ではPositional Encodingを入れることでシーンの高周波成分がきれいに描画できていることを示しています。(出典:https://arxiv.org/pdf/2003.08934.pdf)

Hierarchical Volume Sampling

モデルは視線ごとに学習を行います。
学習画像内のピクセルについてその視線方向上の点を複数点選出します。それらの点についてモデルに座標と視線方向の情報を入力して各点の色と密度を計算します。
これらの色・密度情報からVolume Renderingを施すことでピクセルの輝度値を見積もることができます。この推論された輝度値と元のピクセルの輝度値の残差が小さくなるように学習を繰り返すことでモデルを更新していきます。

$$\mathcal{L}_{\rm{photo}} = \frac{1}{n}\sum_{i=1}^{n}\sum_{p}\lVert{I_{i}(\bf{p}) - \hat{I}_{i}(\bf{p};\theta)\rVert}_{2}^{2}$$

より詳細なRadiance Fieldを獲得する手法として、視線方向上の点をサンプリングする手法についてHierarchical Volume Samplingというアイディアがあります。
モデルは学習の初期段階ではまだどこに「もの」があるかわかっていません。そこで視線を等間隔に切り分けてその区間からランダムに点を選出します(図2.5.a)。これにより粗いレンダリングをすることができ学習が進むにつれて、どこに「もの」があるのかが明確となります。その後、視線方向中から「もの」がある領域を重点的にサンプリングする(図2.5.b)ように変更することで密なレンダリングを行うことができます。

図2.5.a 学習の初期段階ではどこに「もの」があるのか分からないので区間を区切ってランダムに点を選びます。	図2.5.b 学習の後半ではどこに「もの」があるのか分かってきてるので、密度が高い領域をより密に点を選び出します。これによりより詳細なレンダリングが可能になります。

NeRFの問題点

以上がNeRFのアイディアで画像群からシーンを学習する手法です。
NeRFは前述の通り高密度な画像郡がないとモデルは簡単に過学習を起こしてしまい。カメラポーズが正確でないとVolume Renderingや視線の抽出で不整合が生じます。それぞれの問題に独立でアプローチした手法はこれまでにも提唱されてきましたが、今回紹介するSPARFはそれらを同時に解決したというもので、つまり少ない画像でカメラポーズが不正確でもシーンを学習できるというものです。

SPARF

SPARFの学習について基本的な戦略はNeRFと同じですが、カメラパラメータ$\mathcal{P}$も同時に学習を行います。

$$\mathcal{L}_{\rm{photo}}(\theta,\hat{\mathcal{P}}) = \frac{1}{n}\sum_{i=1}^{n}\sum_{p}\lVert{I_{i}(\bf{p}) - \hat{I}_{i}(\bf{p};\theta, \hat{P_{i}})\rVert}_{2}^{2}$$

以下ではSPARFの重要なアイディア２つについて紹介をいたしますが、その前にSPARFでは学習時に深度を利用するので確認をしておきます。深度はNeRFの時点で計算することができていて密度と透過率の積の重ね合わせで表現できます。

$$z({\bf{r, d}})=\int_{t_{n}}^{t_{f}} t \cdot T(t) \cdot \sigma({\bf{r}}(t))dt$$

Multi-View Corresponding

まずはMulti-View Correspondingです。
これは同じシーンを撮影した２枚の画像について同じ"点"を被写体に捉えていたとします。このとき、片方の画像の"点"の画像座標から３次元空間中の対応する世界座標を計算することができます。この"点"について世界座標からもう一方の画像座標に変換したときに"点"の座標を正しく計算できているか評価します。これによりNeRFの学習とカメラポーズの校正をすることができます。

$$\mathcal{L}_{\rm{MVCorr}}(\theta,\hat{\mathcal{P}}) = \sum_{{\bf{p}}\in\mathcal{V}}\mathcal{L}_{{\bf{p}}}$$

$$\mathcal{L}_{\mathbf{p}} = w_{p}\rho \left( \mathbf{q} - \pi \left( \hat{P}_{j}^{-1}\hat{P}_{i}\pi^{-1} \left( \mathbf{p}, \hat{z}(\mathbf{p};\theta, \hat{P}_{i}) \right) \right) \right)$$

ただし$\rho(\cdot)$はHuber Lossです。

図3.1　Multi-View Correspondingのイメージ図。　二枚の画像i, jから黄色いバツを観測したとき、画像iに映るバツの座標を世界座標に対応させて画像jに投影する。それが画像jに映るバツの座標との距離が0になるように学習を進める(出典:https://github.com/google-research/sparf)

このとき、二つの画像内で同じ"点"であることを確かめるためにPDC-Netと呼ばれる外部モデルを使用しています。

Improving Geometry at Unobserved Views

また過学習を回避するために擬似的に新しい視点を用意して、その視線の深度とNeRFから再構成される深度が一致するように学習を進めるImproving Geometry at Unobserved Viewsという手法を提案しています。この過程により新しい視点を再構成しても不整合が起こりづらくなります。

$$\mathcal{L}_{\rm{DCons}}(\theta) = \sum_{p} \gamma_{y}\rho(z_{y} - \hat{z}({\bf{y}};\theta,P_{\rm{un}}))$$

図3.2　Improving Geometry at Unobserved Viewsのイメージ図。学習画像にない新しい視点を用意し座標変換により疑似深度マップを生成。NeRFモデルと新視点のカメラパラメータから生成される深度マップとの残差が小さくなるように学習する。(出典:https://github.com/google-research/sparf)

上記3つのLossを同時に最小化することでNeRFとカメラポーズを同時に学習していきます。

$$\mathcal{L}(\theta,\hat{\mathcal{P}}) = \mathcal{L}_{\rm{photo}}(\theta,\hat{\mathcal{P}}) + \lambda_{c}\mathcal{L}_{\rm{MVCorr}}(\theta,\hat{\mathcal{P}}) + \lambda_{d}\mathcal{L}_{\rm{DCons}}(\theta)$$

実際に使った感想・次回への結び

SPARFの手法の紹介については以上ですが、コードが公開されているので動かしてみた感想についても触れておきたいと思います。私の環境ではRTX4090で10万回イタレーションで14時間の学習時間を要しました(BatchSizeやその他設定はgitで公開されているものを採用しています)。

図4.1	学習で使用した3枚の画像	↑

(参照:https://roboimagedata2.compute.dtu.dk/data/text/multiViewCVPR2014.pdf)

出来上がったシーンがgifの通りで確かに過学習や不整合が起こっていなそうなことが確認できます。

図4.2.a 学習で得られたシーン	図4.2.b　学習で得られた深度マップ

論文中でもA100環境の10万回イタレーションで10時間とあるので、少ない枚数といえどやはり通常のNeRF同様計算に時間がかかってしまうようです。

実際アプリケーションでの利用を考える際、今回の論文では触れてこなかった学習時間はネックになってしまいます。NeRFの高速化についてはすでにたくさんの研究がなされており、SPARFでもそれらアイディアは踏襲できる可能性があると筆者は主張していますが、現状は半日程度の学習時間が必要なようです。

そんな中3D Gaussian Splattingという高速で三次元シーンを学習可能な手法が提案されました。まだ詳細については読めていないのですが、次回はこちらの手法について調査しても良いかもしれません(**)。