論文:限られたリソースでどのように推定し、制御すべきか?―リソースが制限されたシステムにも適用可能な部分観測制御理論の構築―
博士過程の鳥取さんの論文が公開されました。2本関連した論文なので合わせて解説したいと思います。
今回も広報でボツになったプレスリリース用の文章をちょっと改変したものです。理論としての汎用性にフォーカスした形で書いています。
研究のポイント
◆ リソースが制限されたシステムにも適用可能な部分観測制御理論を構築しました。
◆ 平均場制御理論の技法を応用することで最適な制御器を設計するアルゴリズムを構築しました。
◆ リソースの制限が顕著な小型デバイスの制御設計や生物システムの行動原理の解析に寄与することが期待されます。
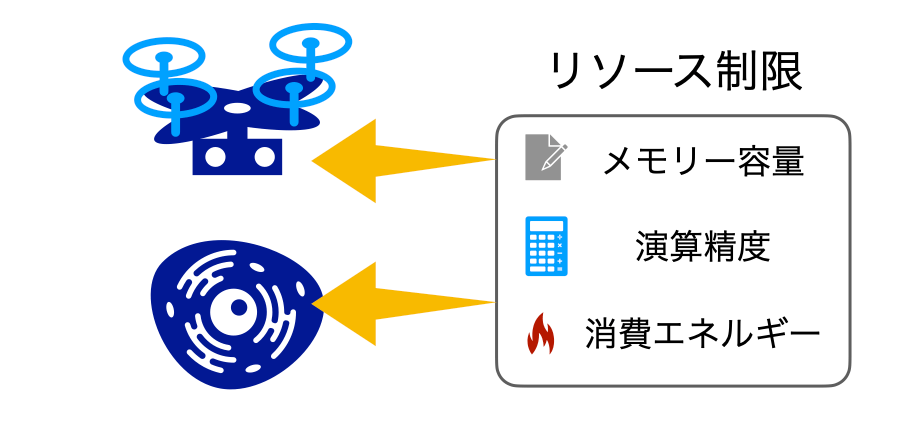
図1 推定・制御問題におけるリソースの制限
不確定な情報から状態を推定し、制御する問題では、一般に情報を記憶するメモリー容量や演算の正確性、消費エネルギーに制限がある。制御対象のみならず制御を実現する制御器側のリソース制限を考えた最適化が現実問題では重要になる。
研究概要
制御対象を正確に観測できない状況下で、不確定な情報から対象の状態を推定し最適な制御を実現する制御器を設計することは工学において普遍的な課題であり、古くから部分観測制御理論として研究されてきました。しかし、部分観測制御理論は無限のリソースを制御器に使える理想的な状況を前提として構築されています。一方で、現実問題では、制御器の記憶のサイズや演算の正確性、そして動作時のエネルギーコストのようなリソース制約が必ず存在します(図1)。そのため、それらが特に顕在化する小型デバイスや生物システムなどのシステムに部分観測制御理論を直接応用することが困難であるという理論的な課題がありました。
博士2年の鳥取さんは、リソースが制限されたシステムにも適用可能な新しい部分観測制御理論を構築しました。また平均場制御理論[1]の技法を応用することで、最適な制御器を設計するアルゴリズムの構築にも成功しています。この理論は、リソースの制限が無視できない小型デバイスの制御設計や生物システムの行動原理の解析に寄与することが期待されます。
研究の詳細
研究背景
「制御対象を望むように制御する最適な方法は何か?」は工学の多くの局面で現れる普遍的な問題です。また多くの状況では制御対象の状態を完全に観測することができないため、対象の状態を最適に推定し、かつ最適な制御も実現する制御器を設計することが求められます。部分観測制御理論はこのような最適推定と最適制御の複合的な問題を解くための理論であり、特に、最適推定は機械学習でも有名なベイズ推定で与えられることが知られています。
しかし、従来の部分観測制御理論では、設計される制御器が持つリソースの制限が全く考慮されていません。具体的には、無限の記憶容量を持ち、演算が正確な制御器が想定され、制御器を動作させるときに発生するエネルギーコストも考えられていませんでした(図1)。このような設定は、十分な計算機リソースと理想的な動作環境を制御器に仮定できる大型システムの制御問題であれば近似的に実現可能ですが、ドローンなどの小型デバイスや極限環境下で動作する探査ローバーの設計では現実的でありません。加えて、細胞など、単純でリソースの制約が大きいにも関わらず高度な振る舞いを示す生体の設計原理を理解する上でも部分観測制御理論は不十分なものです。
研究内容
博士課程2年鳥取さんは、平均場制御理論の技法を応用することで、リソースが制限されたシステムにも適用可能な新しい部分観測制御理論を構築しました。
1. リソースの制限を考慮した部分観測制御問題の定式化
従来の部分観測制御理論では、ノイズの乗った制御対象の観測からベイズ推定に基づいてその状態を最適に推定しますが、ベイズ推定を実行するには一般に無限の記憶容量と正確な観測情報の演算処理が必要となります。実際の制御器は記憶容量や演算処理の精度に制約があるため、実装する段階でベイズ推定を有限の記憶容量で近似するアドホックなプロセスなどが介在します(図2青)。その結果、実際に作られたシステムが与えられた制約の元で最適であるのかは保証されなくなります。また制御器自体の動作エネルギーコストもベイズ推定では考慮されません。
これに対し本理論では、利用可能な記憶のサイズや演算の精度に基づいて制御器の可能な動作を定式化した後に、動作コストを考慮して制御器の動作を最適化することで、リソースが制限された状況下でも最適な推定と最適な制御を実現します(図2橙)。このような問題の定式化により、本理論は従来の部分観測制御理論の持つ課題を克服しています。

図2 従来の理論(青)と本理論(橙)の対比
従来の理論(青)では最適化から理想的な制御器を求めた後に、実際の制御器のリソース制限を満たすようにアドホックな近似を使用するため、最適性が保証されない。本理論ではリソース制限に基づいて制御器の動作を定式化した後に最適化するため、最適性が保証される。
2. 平均場制御理論の技法を応用したアルゴリズムの提案
従来の部分観測制御理論では、最適な制御器を設計する問題が現代の計算機でも解くことが現実的に不可能な汎関数微分方程式に帰着してしまう問題があり、最適な制御器を実用的に設計することが困難でした。
本理論では、平均場制御理論の技法を応用することで、最適な制御器を設計する問題が現実的に計算可能な偏微分方程式に帰着できることを明らかにしています。さらに最適な制御器が満たすべき条件が確率空間上のポントリャーギンの最小原理[2]に対応することを示すことで、最適な制御器を設計するアルゴリズムとして前向き後向きスイープ法[3]を提案しました。一般に前向き後向きスイープ法は収束性が保証されず解が必ずしも求まらないことが知られていますが、本理論は前向き後向きスイープ法の収束性が保証される性質の良い特殊なクラスであることも明らかにしました。
3. 線形二次ガウス問題における部分観測制御理論との整合性
線形二次ガウス問題[4]は部分観測制御理論で盛んに研究されている問題であり、有限の記憶容量でも最適推定と最適制御を実現することができるため、記憶サイズが制限されたシステムにも適用することができます。本理論では、線形二次ガウス問題において、カルマンフィルタやリカッチ方程式など、部分観測制御理論と全く同じ結果を再現できることを明らかにしました。この結果は本理論が従来の部分観測制御理論と整合性のある妥当性の高い理論であることを示唆しています。加えて本理論では、従来の部分観測制御理論では十分に議論することができなかった、記憶サイズなどのリソースが制限された非線形二次ガウス問題にも適用することができ、優れた性能を発揮できることを明らかにしました(図3)。

図3 従来の理論(青)と本理論(橙)を比較した数値実験
利用可能な記憶サイズが制限されたもとで、不確定な情報から状態を推定し、障害物を回避して目的地へ到達する制御を実現する問題を考える。従来の理論(青)では制限された記憶サイズで障害物を回避することができないのに対して、本理論(橙)では回避することができる。
今後の予定
集約化・大規模化を原動力とした20世紀の工学技術に対し、現代技術や社会が直面する様々な課題では小規模分散的なアプローチの重要性が高まっています。ドローンのような小型デバイス群の制御は一例です。このような小型デバイスに搭載できる記憶容量は限界があり、消費されるエネルギーも少ないほど望ましいと考えられます。一見困難に見える課題ですが、生体システムに目を向けると単細胞から多細胞生物まで、極めて限定されたリソース、確率的な挙動が不可避な細胞内反応、そして工学システムと比較して大幅に少ないエネルギー消費で高度な機能が実現されています。本理論は、リソース制約のある制御システムの設計のみならず、従来の理論では困難だった生体機能の設計原理の解明にも活用することが可能であり、今後、生命の普遍的法則の解明と生体模倣工学の両面に貢献することが期待されます。
-
平均場制御理論: 非常に多数のエージェントが相互作用するシステムを制御するための理論。平均場制御理論では、エージェントの集団の影響がエージェントの確率で近似的に表現できるため、確率を制御することが重要になる。リソースの制限を考慮した部分観測制御理論では、推定を最適化するために確率を制御することが重要になるため、平均場制御理論が有効なアプローチになる。 ↩︎
-
ポントリャーギンの最小原理
確定システムの最適制御問題の代表的解法。ポントリャーギンの最小原理では、最適な制御器を設計する問題が時間前向きダイナミクスと時間後向きダイナミクスの二点境界値問題に帰着する。平均場制御問題は確率を状態とする確定システムの最適制御問題として解釈することができるため、確率空間上のポントリャーギンの最小原理が有効なアプローチになる。 ↩︎ -
前向き後向きスイープ法
ポントリャーギンの最小原理の代表的解法。ポントリャーギンの最小原理では、最適な制御器を設計するために、時間前向きダイナミクスと時間後向きダイナミクスの二点境界値問題を解く必要がある。前向き後向きスイープ法では、時間前向きダイナミクスと時間後向きダイナミクスを交互に計算することで、二点境界値問題の解を求める。 ↩︎ -
線形二次ガウス問題
ダイナミクスが線形で、コストが二次関数で、ノイズがガウス分布で与えられる問題。線形二次ガウス問題は最適制御理論が準解析的に解ける性質の良い特殊なクラスであるため、非常に多くの研究がなされている。 ↩︎
Discussion