📝

論文：非平衡化学反応系の情報幾何学構造

2022/09/17に公開

システム生物学

平衡の化学反応熱力学の情報幾何学構造に続き、非平衡の化学反応熱力学の新たな情報幾何学構造に関する論文がPRRで公開されました。この構造はこれまで情報幾何で明示的に意識されていなかった新しいものと考えています。

背景

様々な工学システムが電気回路を集積したシステムであるように、生体システムは化学反応の回路を集積したシステムです。様々な生体機能は化学反応回路システムによって実現され、その多くは反応システムの非平衡性と結びついていることが示唆されています。

非平衡化学反応熱力学の理論化の試み古く、オンサーガもその論文で化学反応を取り上げ、またプリゴジンも化学反応系を主要な対象として研究をしてきました。と同時に、化学反応系は様々な非平衡理論や原理、例えば最小エントロピー生成原理などが成り立たない事例としてもしばしば取り上げられます。
非平衡として化学反応を取り扱う時の難しさの一つは、熱力学的力 $f$ と流れ $j$ の間の関係にあります。線形電気回路の理論や平衡近傍のオンサーガ相反関係においては、力と流れの間に線形でかつ正定値対称な関係

I=R \Delta V, \qquad j=L^{*} f

が成り立ちます。正定値性は力と流れの積で表されるエントロピー生成 $\dot{\Sigma}=\langle f, j\rangle$ が非負である熱力学的要請に基づきます。ここから力と流れの双対空間に内積構造が誘導されます。
一方化学反応ではこの力の流れの関係がlogを含む非線形なものになります。これが平衡近傍で広く成り立つオンサーガの関係を非平衡に拡張する上での一つの障害でした。

結果：非平衡化学反応系におけるヘッセ・情報幾何学構造

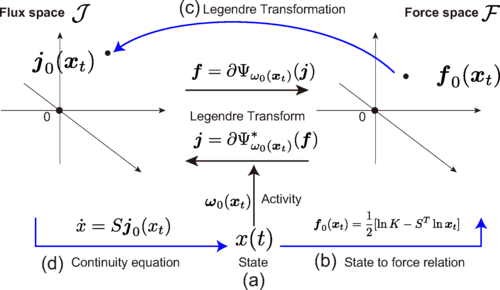
歴史的に非線形関係を解消する試みはいくつかありますが、我々は力の流れの関係を散逸関数が誘導する非線形なLegendre変換(以下ヘッセ構造)として捉えるアプローチを取りました。

散逸関数が誘導するヘッセ幾何学構造と一般化勾配流

力と流れの関係を散逸関数を凸関数として持つLegendre変換として表すと、Legendre変換により力と流れの空間 $(\mathcal{J},\mathcal{F})$ のペアに情報幾何学的双対平坦構造が誘導されます。
また散逸関数の持つ追加的な性質(非負性・対称性)から、Legendre変換が誘導する非線形双対構造を内積の線形双対構造の一般化としてみることができます。

双対平坦構造

そして、質量作用化学反応の平衡ダイナミクスは、リーマン多様体上の勾配流における内積をLegendre変換に置き換えた一般化勾配流として特徴づけることができ、勾配流を誘導するポテンシャル関数は状態空間上の一般化カルバックライブラー情報量になります。
そしてこの勾配流構造は、状態空間における分子濃度と化学ポテンシャルの双対平坦構造 $(\mathcal{X},\mathcal{Y})$ と整合的で、平衡反応における全系エントロピー差とエントロピー生成の等式を導きます。
非平衡でもこの構造は有効で、平衡・非平衡に関わらず質量作用化学反応のダイナミクスは平衡流を誘導する勾配力をシフトしたものとして表すことが可能です。

一般化勾配流

一つ前の論文で示した状態空間 $(\mathcal{X},\mathcal{Y})$ 上の双対平坦構造は、一般的な情報幾何学と類似のもので、有限次元確率分布の場合には、確率分布とその対数 $(p, \ln p)$ の双対性になります。化学反応であれば濃度と化学ポテンシャル $(x, \mu)$ の双対性です。

一方今回の論文で示した情報幾何学構造は、力と流れ $(\mathcal{J},\mathcal{F})$ の間の双対平坦構造で、これは上述の状態空間 $(\mathcal{X},\mathcal{Y})$ 上の構造とは、基本的には別物であり、それぞれを誘導する凸関数も別物です。
状態空間の場合はいわゆる系の自由エネルギーなどの熱力学的ポテンシャル関数。力・流れ空間の場合は散逸関数です。
特に力・流れ空間の双対平坦構造はこれまで情報幾何学でも扱われてこなかった新しいものになります。

情報幾何学構造に基づくダイナミクスの分解

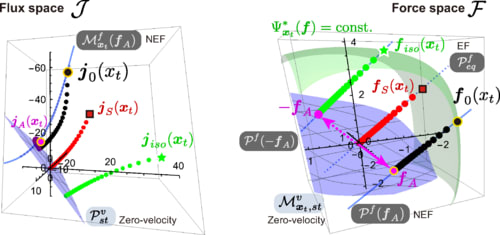
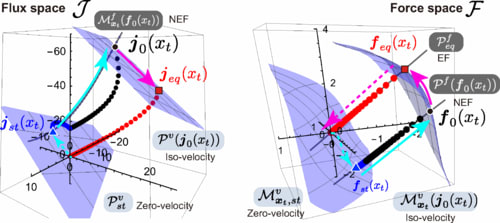
この非平衡流やそれに伴うエントロピー生成を分解するのに、力・流れ空間に誘導されたヘッセ・情報幾何構造を内積構造の代わるものとして活用することができます。内積空間であれば分解には直交射影を用いますが、内積空間ではないヘッセ・情報幾何学構造においては、直交の概念が拡張されることになります。

散逸関数の作る中心アファイン多様体に基づく一般化ヒルベルト直交性を用いた分解からはHatano-Sasa分解の化学反応版が導かれます。これは化学反応理論で古くから知られていたHorn-Jacksonのcomplex balanced 状態(非平衡定常状態の一種)が一般化カルバックライブラー情報量をリアプノフ関数として持つことの情報幾何学的な意味を与えます。

ヒルベルト直交性

一方で情報幾何学で一般的に用いられる双対平坦構造と一般化ピタゴラスの定理に基づく分解は、連続多様体上のベクトル場(内積空間の要素)を分解するヘルムホルツ・ホッジ・小平分解の情報幾何学的な一般化を与えます。熱力学的にはこの分解からMaes-Netocny分解の化学反応版が得られました。そして、この分解で得られる射影された力や流れは一般化ピタゴラスの定理を介して、最小散逸流れや最小散逸力として変分的に特徴づけることができます。

情報幾何学的直交性

今後の展開

このLegendre双対による力と流れの関係は、拡散過程やFPEのような連続多様体上の流れの場合は、2次の散逸関数が誘導する内積構造に帰着し情報幾何学は不要です。むしろ $L^{2}$ -Wasserstein幾何に結びつきます。しかし、化学反応やジャンプ過程のような離散多様体(グラフなど)上の流れや非線形流においては、このヘッセ・情報幾何学構造が本質的になると考えています。

実際、熱力学的不確定性原理(TUR)の理論では、拡散過程であればTURのtight boundがエントロピー生成になるのにも関わらず、グラフ上のジャンプ過程など離散的な状態を持つ確率過程ではエントロピー生成がtight boundにならず、代わりに疑エントロピー生成がtight boundとしてもとまっています。論文では、この疑エントロピー生成が流れと力の空間上のフィッシャー情報量と結びついていることを言及しています。散逸関数が2次型であれば、エントロピー生成率とフィッシャー情報量のギャップは生まれませんが、より一般の凸の場合にはギャップができます。したがって、離散確率過程のTURのギャップはヘッセ・情報幾何構造の顕在とみなすこともできると思われます。

オンサーガー関係、プリゴジンの最小エントロピー生成原理、線形電気回路理論、そして60年代のHillや他の研究者によるネットワーク熱力学の試みなどはすべて、力の流れの間の線形関係に強く依存しており、それ故に線形を超えた領域への拡張は当時達成されませんでした。今回の結果はこの問題が、Legendre変換と双対平坦な情報幾何学構造で打開できる可能性を示唆します。
またこの理論は、化学反応システムの熱力学的構造や性質を捉えるのに活用できるだけでなく、新たな情報幾何や力学系の数理構造を与えます。
今後化学反応にとどまらないこの理論の応用を探求していきたいと思っています。