Waddington地形の数理基礎としての一般化勾配流構造

博士過程の堀口さんの論文が公開されました。

https://journals.aps.org/prresearch/abstract/10.1103/PhysRevResearch.5.L022052

この話は、古くは発生生物学の流れで提唱され、最近は1細胞シーケンスなどで頻繁に取り扱われるようになったWaddingtonランドスケープを一般化勾配流で位置づけるものです。特に、一般に流布しているWaddingtonランドスケープの解釈や関連するポテンシャル描像は不完全であり、一般化勾配流構造がそこを埋める数理的基礎であることを示したものです。少し玄人向けですが、生物物理学や理論生物学の観点から極めて重要な内容だと思っています。

研究のポイント

◆ Waddingtonランドスケープにおける1細胞と細胞集団の関連性が一般化勾配流構造でつながることを明らかにした。
◆ T細胞免疫集団の応答などがこの一般化勾配流構造に一致していることを示した。
◆ 発生を含めた多細胞動態のロバスト性や最適性の理解だけでなく、新たな集団動態推定手法の開発に寄与することが期待される。

研究背景

発生過程に代表されるように、多くの多細胞集団のダイナミクスは集団としての高い再現性やロバストを示します。これはあたかも事前にプログラムされた発生経路を集団がたどるように変化しているととらえられます(図1左)。これは専門用語的にはhomeorhesisと表されます。この集団としてのロバストなダイナミクスは1細胞レベルでの遺伝子発現(表現型)変化によって担われており、　有名なWaddingtonランドスケープ (以下、表現型地形)では、1細胞を表すボールが地形を転がり落ちる形で表現型の変化が表されています(図1右)。この表現型地形の中でボールが転がり落ちる描像が細胞分化の不可逆性などと紐付けられたりします。その関係で、1細胞RNAseqなどで推定された発生経路を表現型地形と結びつけて議論することが特に最近行われています。

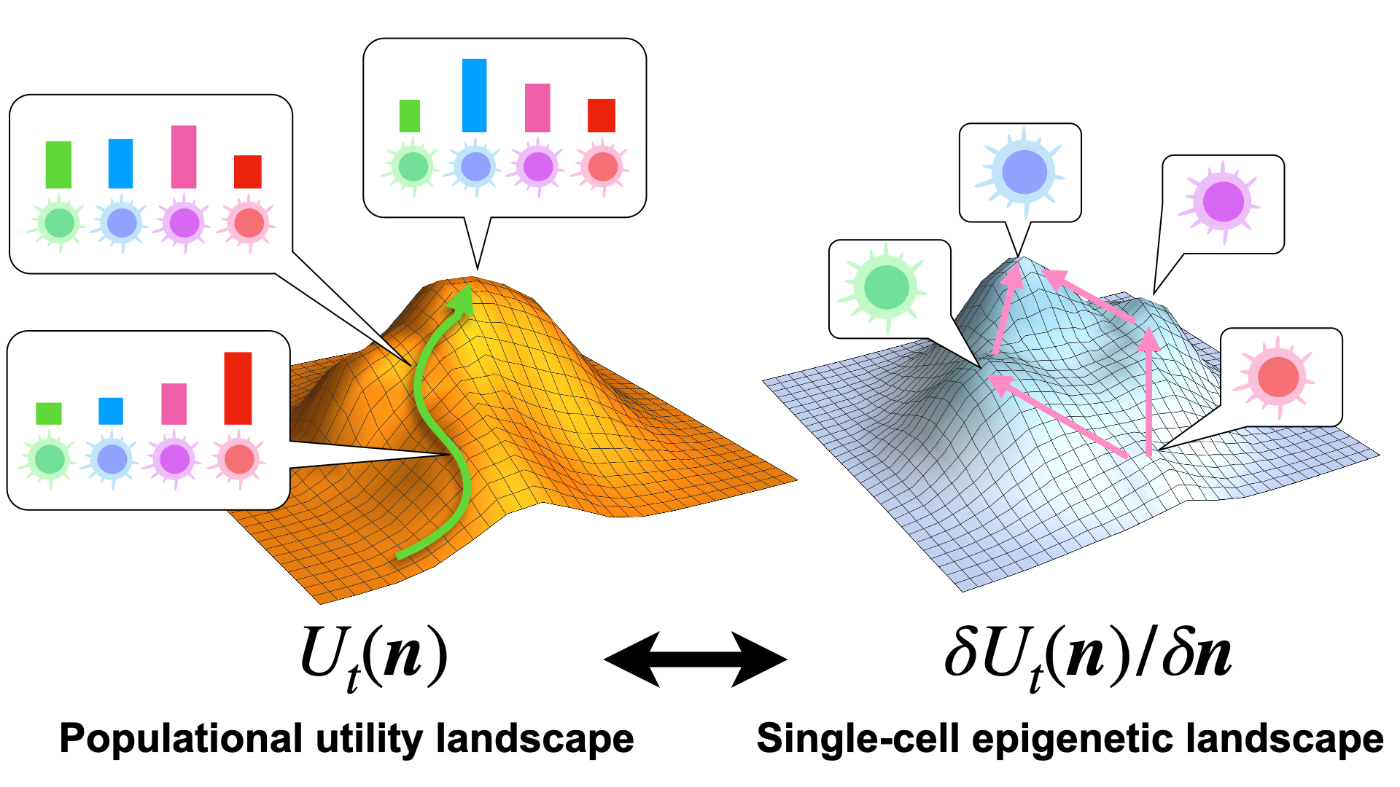
図1　集団の発生地形と1細胞の表現型地形の関係性：ここではダイナミクスは上がる方向に進行するとしている

しかしよく考えるとこの理解には多くの不可解な点があります。まず細胞集団としての発生がロバストに進むには、多数の異なる表現型の細胞種が適切な割合で形成されなければなりません(発生なら更に空間的位置も大事)。これは集団内の多種の細胞の相互作用が不可欠です。しかし1細胞が表現型地形を転がり落ちる描像は、1つの細胞がある経路を地形に沿って(不可逆に)落ちてゆくことだけが記述されていて、その地形自体が細胞集団の相互作用によりどのように形成されるかについては覆い隠されてしまっています。また当たり前ですが、発生などの進行に従って集団内の細胞種の割合が変化すればこの地形は動的変化すべきです。そしてその動的な変化は、集団としての発生のロバスト性を実現するようにできていなければなりません。
すると本来ランドスケープ的な描像に従って(ロバストに)時間発展するべきなのは細胞集団の状態であり、1細胞が必ずしもランドスケープ的であるべきかかどうかは自明ではありません。

つまり、集団レベルの発生経路のロバスト性と1細胞レベルの分化経路のロバスト性の2つが絡み合っており、更にそれらを捉えるべき集団の発生ランドスケープ(以下発生地形)と1細胞の分化ランドスケープ(表現型地形)が存在することが示唆されるわけです。では、

• この集団と1細胞の2つのランドスケープ(発生地形 vs 表現系地形)はどう関連しているのか？
• そもそもランドスケープ的な1細胞の振る舞いは集団としてのランドスケープ的な振る舞いに必要なのか？

などの問題が生じます。scRNAseqに基づく発生経路の推定などが最近盛んですが、これらの集団と1細胞の構造の本質的な違いや関係性には無自覚で、素朴に1細胞の表現型地形と集団の発生地形を同一視しているようにも見受けられます。

研究内容

博士課程3年堀口さんは、一般化勾配流の概念と使うことで集団の発生地形と1細胞の表現型地形の関係をとらえる理論を構築しました。この理論は物理で言うところの、化学ポテンシャル(1分子ごとのポテンシャル)と熱力学的ポテンシャル(分子集団のポテンシャル=系の自由エネルギー)の関係を一般化したものであり、物理的な観点からも極めて自然な概念になっています。

１． 一般化勾配流による集団動態ロバストネスの定式化

この理論では計算論的生物学の発想に基づいて、まず細胞集団が実現したい動態を規定する要素として集団の効用関数$U(\boldsymbol{n})$を仮定します。状態$\boldsymbol{n}_{0}$からスタートした集団は$U(\boldsymbol{n})$がなるべく大きくなるような集団状態に進行したいとします。しかし集団の細胞種の割合$\boldsymbol{n}$を変化は細胞分化や細胞増殖、細胞死などで誘導され

$$\frac{\mathrm{d}\boldsymbol{n}}{\mathrm{d}t}=\mathrm{Diag}[\boldsymbol{g}]\boldsymbol{n} + \mathbb{T}\boldsymbol{n} + \boldsymbol{m}$$

それらは一定のコストを持ちます。これらのコストは凸関数$C(\boldsymbol{g},\boldsymbol{m},\mathbb{T})$で表されます。ここで$\boldsymbol{g}$,$\boldsymbol{m}$,$\mathbb{T}$は各細胞種の増殖、移流、表現型変化の速度を表し、増殖や表現型変化が頻繁に起こるほど大きくなります。
$U(\boldsymbol{n})$がなるべく大きくなるように集団の状態が変化しつつ、変化を誘導するのに必要なコスト$C(\boldsymbol{g},\boldsymbol{m},\mathbb{T})$が最小化される軌道として最適な集団発生軌道$\boldsymbol{n}_{t}$を考えます。この集団発生軌道は一般化勾配流と呼ばれるもので、この軌道$\boldsymbol{n}_{t}$に沿って$U(\boldsymbol{n})$は増加します。

2． 一般化勾配流が誘導する1細胞レベルの表現型地形

では最適な集団発生軌道$\boldsymbol{n}_{t}$を実現するために1細胞はどのように振る舞うべきでしょうか？一般化勾配流構造から、1細胞の増殖率や表現型の変化率などは集団効用関数$U(\boldsymbol{n})$の変分である$\boldsymbol{\mu}(\boldsymbol{n})=\delta U(\boldsymbol{n})/\delta \boldsymbol{n}$の大小に依存して$\boldsymbol{\mu}$の大きい細胞状態に変化します。
つまり$\boldsymbol{\mu}(\boldsymbol{n})$が1細胞での表現型ポテンシャルとして機能し、自然とポテンシャルに依存したダイナミクスが1細胞レベルで要求されることがわかります。具体的には、よりポテンシャルが大きい細胞状態への遷移が変化が不可逆的に誘導されることになり、細胞分化における不可逆性などの性質が導かれます。

3． 一般化勾配流と化学熱力学との類似性

細胞集団の一般化勾配流構造は化学熱力学との類推で言うと、$U(\boldsymbol{n})$が(多数の化学分子で構成される)系の熱力学的ポテンシャル(自由エネルギー)、$\boldsymbol{\mu}(\boldsymbol{n})$が個々の分子の化学ポテンシャルに対応します。一般化勾配流が誘導する軌道$\boldsymbol{n}_{t}$は熱力学的ポテンシャルが最小化する平衡状態へ収束する軌道の一般化であり、この軌道$\boldsymbol{n}_{t}$は化学ポテンシャル$\boldsymbol{\mu}(\boldsymbol{n})$の差に依存して個々の反応(個々の細胞の表現型変化や増殖)が起こることによって実現します。
したがって一般化勾配流の数理構造を活用することで、発生のロバスト性や不可逆性がある種の熱力学系のアナロジーでとらえられることがわかりました。

ここでの話は、熱力学的な定式化とはそのままは合致しないことに注意が必要です。例えば細胞の分化過程は平衡ではないですし、完全に不可逆な状態変化も粗視化レベルによっては現れます。そして、集団動態が最終的に実現する状態も普通は非平衡状態です。ここではこのような不可逆や非平衡状態を含むように勾配流構造を拡張した一般化勾配流の構造が必要になります。また、個々の細胞種の表現型ポテンシャル$\mu_{i}(\boldsymbol{n})$は一般に自分と同種の集団数$n_{i}$だけでなく、他の細胞種の集団数にも依存します。これは希釈化学反応系などと大きく異なる点でもあります。

4． 免疫T細胞集団の応答と一般化勾配流構造

では実際の細胞集団はこの一般化勾配流構造を持つのでしょうか？
元々Wadington地形は発生現象を動機として提起されたので発生現象で検証できればいいですが、発生では細胞種の割合だけではなく空間的位置関係なども重要になり、直接理論を適用するには適切ではありません。そこで空間構造の重要性が発生よりも低い免疫集団の集団応答を対象としてその一般化勾配流構造を調べました。実際に図2で示すように、感染依存的に誘導されるT細胞集団の表現型変化ダイナミクスが(近似的に)一般化勾配流構造を持っていることを示しました。

図2 T細胞集団モデル(a,b)の持つ一般化勾配流構造(c)。

今後の予定

近年のsingle cell RNA seqの技術発展などによって細胞集団内の表現型状態を1細胞ごとに測ることやその時間的変容が測定できるようになっています。それらのデータを解釈する方法としてWaddigtonランドスケープの概念が活用されていますが、実はその概念の背後には集団の発生地形と1細胞の表現型地形が複雑な関係絡み合っており、現時点での解析などはこの関係性をとらえられていません。我々の理論はこのような定量的な発生動態データの解釈や新たなデータ解析方法の基礎となることが期待されます。

また今回細胞集団に適用した一般化勾配流構造は、非平衡化学反応系や力学的な系を含めたかなり広いクラスの物理系を捉えることができる理論基盤になっています。一般化勾配流構造を基礎とすることで、集団動態と力学的相互作用や個々の細胞の中の化学反応系など一見関連付けが難しい要素を階層的かつ統一的に結びつけることができると期待されます。これにより、集団と化学反応が絡みある生体集団情報処理や力学と集団動態が絡み合う組織発生など、多階層的な生体現象の理解が進むと期待されます。