論文:平衡化学熱力学のもつヘッセ幾何学構造
特任助教の杉山さん、上村さん、研究員のLoutchkoさんの論文が2報ジョイントで公開されました。
以下、広報でボツになったプレスリリース用の文章をちょっと改変してまとめを作成してみました。
研究のポイント
◆ 熱力学第二法則だけから、化学熱力学が持つ普遍的なヘッセ幾何学的構造を導いた。
◆ 化学熱力学系を特徴づける諸量がヘッセ幾何構造と自然に対応づくことを示した。
◆ 化学反応で形作られる細胞などの生体システムが、熱力学の法則にどう制約されるのかを明らかにするための理論基盤になる。
研究概要
熱力学は、対象とする物理系の詳細から切り離された形で構成される物理学においても非常に普遍性の高い理論的な枠組みです。平衡熱力学の体系は100年以上前に確立され様々な分野に応用されていますが、化学反応系においては平衡熱力学の成立と同時期に質量作用の法則に代表される具体的な反応速度論が見いだされたこともあり、熱力学と速度論が混在して研究が進んできました。特に近年、生物現象への応用を背景として化学反応系の熱力学が注目されていますが、その多くは特定の速度論(質量作用の法則に従う反応系)に立脚し導かれています。しかし本来熱力学的結果に速度論的な情報は不要です。その結果、これまでに得られた結果などが純粋に熱力学から導かれるものなのか、それとも仮定した特定の反応速度則等に限定されるものなのかを区別することが難しく、熱力学の法則と反応速度論が峻別されず混在した形で理解されることも多かったと考えています。
我々は論文(1)で、速度論を仮定して得られていた平衡化学熱力学の既存の知見が、熱力学第二法則だけを仮定した純粋に熱力学的な方法で導かれることを示しました。この過程で、化学熱力学に内在する幾何学構造(ヘッセ幾何構造)を数理的に明らかにし、平衡状態の存在や唯一性、平衡状態の緩和に伴うエントロピー生成などの問題が幾何学的な変分問題(最適化問題)として特徴づけられることも示しました。
また論文(2)では、質量作用の法則を仮定するとこの幾何学構造が一般化KL Divergenceや指数型分布族を誘導する凸関数による双対平坦構造に帰着し、反応系特有の代数制約から代数統計で用いられる拘束付き統計モデルや実トーリック幾何学と関連することなどを示しています。
論文(1)の結果は反応速度論に依存せず成り立ち、したがって反応の速度論的性質等が必ずしも明らかではない複雑な化学反応から構成される細胞など生体システムに対して、熱力学体系の理論的な基礎を与え、その制約を明らかにできることが期待されます。また、指数型分布族以外の作る幾何構造を探索する対象として、質量作用則以外の広いクラスの反応系があり得ることを示し、情報幾何学と化学反応系の新たな関係性を提供すると考えています。

研究の詳細
研究背景
熱力学は100年前に成立した普遍的な理論体系です。特に、第二種永久機関の実現不可能性から、平衡状態はエントロピー関数を最大にする状態として特徴付けられます。これは化学反応も含む一般的な物理多体系で成り立たなければいけません。一方で、化学反応論においては熱力学成立と同時期に質量作用の法則に代表される速度論が確立しました。速度論の観点からは、平衡状態は全ての反応の流れが無くなる詳細釣り合い状態で特徴付けられます。この2つの特徴づけは互いに等価です。
近年、確率熱力学の発展や生物応用などを背景に化学反応論の熱力学に注目が集まり、応用数学で見出されてきた化学反応論の知見に熱力学的な意味づけをする研究が行われています。それらの結果の多くは質量作用の法則など特定の速度論に基づいて導かれています。しかし、平衡状態の熱力学的特徴づけと速度論的な特徴づけの等価性を鑑みると、それらの結果がもし熱力学的普遍性をもつものであれば、純粋に熱力学的な議論のみから構成されなければなりません。にもかかわらず、それらの結果は質量作用でのみ成り立つのか、それとも細胞内の反応などの質量作用が成り立たないかもしれないより広い化学熱力学系で成り立つのかは、未解明でした。
研究内容
特任助教の杉山さんを中心とする我々のグループは、熱力学第二法則で仮定されるエントロピー関数の性質のみを用いて、特定の速度論(質量作用則)を仮定して導かれた化学熱力学の諸結果が極めて一般的に導かれうることを示しました。その過程で、化学熱力学が持つ物理的拘束がヘッセ幾何構造によって数理的に表現されることを見出し、その熱力学的重要性を明らかにしました。
1.平衡状態の候補と幾何学的特徴
化学熱力学の難しさは、系の状態である各化学物質の濃度が独立に変化できず、考えている系を構成する様々な化学反応が、到達可能な状態を代数的に拘束する点にあります。その結果、ある初期濃度からスタートした系が到達できる状態はある集合(部分多様体)を作ります。これを化学量論多様体といいます。一方で熱力学に目を向けると、しばしば平衡状態は唯一存在すると思われがちですが、化学熱力学ではこの代数的な拘束により平衡状態の候補も多数現れ、ある集合を作ります。この集合を平衡多様体と呼びます。実現される平衡状態は、これら二つの多様体の共通部分でなければなりません。本研究では、この多様体間の幾何学的関係性がヘッセ幾何学構造をなすことを見出し、共通部分が一点であること、すなわち平衡状態が初期濃度に依存して一意に決まることを示しました。
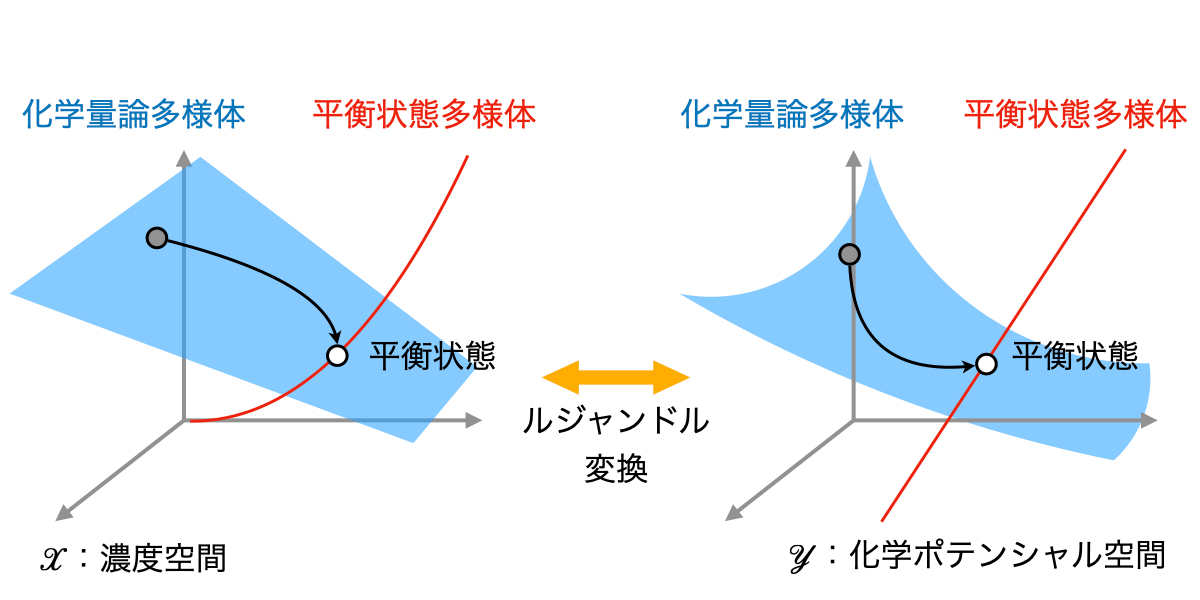
2.熱力学的諸量とヘッセ幾何学の対応関係
ヘッセ幾何学とは、ポテンシャル関数と呼ばれる凸関数から誘導されるルジャンドル双対な二つの空間のなす幾何学です。熱力学に誘導されるヘッセ幾何学構造においては、このポテンシャル関数は系の自由エネルギー(熱力学的ポテンシャル関数)に対応し、二つの空間はそれぞれ濃度空間とそれに共役な化学ポテンシャル空間を意味することを明らかにしました。また、平衡状態への緩和で生じるエントロピー生成が、ポテンシャル関数から幾何学的に定義されるBregman擬距離に一致することを示しました。さらに平衡状態の一意性は、一般化されたピタゴラスの定理を介した変分問題(凸最適化問題)に帰着されることを見出しました。
今回得られた化学熱力学の一般的な幾何学的理論体系において、理想溶液の条件や質量作用の法則などの特定の状況を仮定することで先行研究の結果を再現することを確認し、本理論がそれらを包含する理論体系であることも示しました。さらに同じ幾何学構造は、質量作用の法則と詳細釣り合いによる速度論的平衡状態の特徴づけからも再現されることを明らかにしました。
今後の予定
平衡化学熱力学の一般的な理論体系が構築できたことは、反応の速度論的性質等が必ずしも明らかではない細胞など生体システムに対しても熱力学の理論的な基礎を与え、その制約を明らかにできることが期待されます。しかし本結果は平衡状態の存在と体積が変化しないことを仮定して構築されています。
より一般的な系においては平衡状態が存在しない場合や細胞のように反応に合わせて体積が成長する場合もあります。今後は、このようなより一般な化学熱力学を幾何学的に特徴づけることにより、化学熱力学の一般的な理論体系を完成させることを目指します。
※本研究は日本学術振興会科学研究費助成事業(19H05799, 21K21308), CREST(JPMJCR2011, JPMJCR1927)などの助成や支援を受けて行われた。
Discussion