以下のテキスト Convex Optimization – Boyd and Vandenberghe の第3部 Algorithms(9〜11章)を読みます。今回は9章 Unconstrained minimization(制約がないときの最小化) の冒頭部分(457ページ)をみて、出てくる言葉や数学的主張を確認するところまでです。
https://web.stanford.edu/~boyd/cvxbook/
第3部より前の部分についてはつまみ読みなのでテキストの流れに必ずしも沿っていません。数学的主張に定理番号等がふられていないので適当な名前を付けています。私の誤りは私に帰属します。
凸関数を最小化したい
💛 9章では、最小化したい f: \mathbb{R}^n→\mathbb{R} は凸関数で2回連続微分可能であるとしているね。
💜 f が凸関数であるとは、x から y に割合 \theta だけ歩いた点の値が、(x, f(x)) から (y,f(y)) に張った糸のその点での高さと同じかより小さいということでしたよね。下にたわんでいるイメージです。
凸関数の定義
f が凸関数であるとは、定義域内の任意の x, y と任意の \theta \in [0,1] に対し、以下が成り立つこと。
f( (1-\theta)x + \theta y ) \leqq (1-\theta)f(x) + \theta f(y)
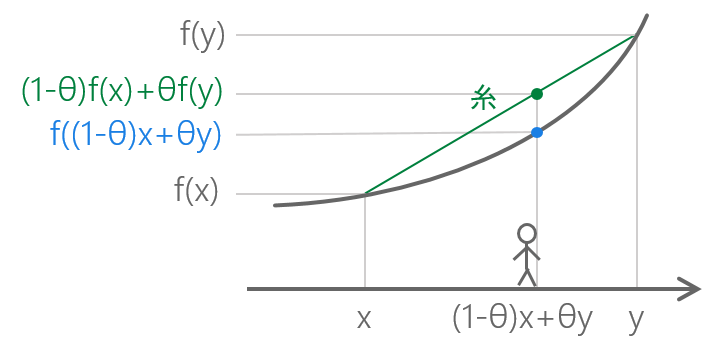
凸関数の定義
💛 うん、そんな f が最小になる点、最小点を探したい。ここで x^\ast が最小点であることの定義は、定義域内の任意の x に対して f(x^\ast) \leqq f(x) が成り立つことだね。9章でやりたいのは、具体的にどうやってこの x^\ast にたどり着くかだ。あ、ここでの仮定として f に最小点 x^\ast は存在することにする。対応する最小値を p^\ast \equiv \inf_x f(x) = f(x^\ast) とおく。
💜 f が凸関数なのに最小点が存在しないことなんてあるんですか? 下にたわんでいるのに?
💛 f(x) = x や f(x) = e^x に最小点はある?
💜 あっ……。f(x) = x や f(x) = e^x に最小点の定義を満たす点はないですね。どんな x をとっても x をもう少し小さくすればもっと値が小さくなりますから。f が凸関数であることと、どこかに最小点があることは違いますね。
凸関数が最小になる点はどんな点
💛 さっそく最小点を探そう。といってもどんな点を探せばいいかだけど、f が微分可能な凸関数ならば、x^\ast が f の最小点であることの必要十分条件は \nabla f(x^\ast) = 0 だ(457ページの式9.2)。
微分可能な凸関数の最小点の必要十分条件(制約がない場合)
f が微分可能な凸関数ならば、x^\ast が f の最小点であることの必要十分条件は \nabla f(x^\ast) = 0。
💛 だから勾配 \nabla f(x) がゼロベクトルであるような点 x を探せばいい。
💜 えっ、うーん……なぜそのような点を探すのでいいんでしょうか。
凸関数の勾配が満たす条件
💛 じゃあ確認しておこう。参照されている 4.2.3 節は 139 ページだね。まず、f が微分可能な凸関数ならば、定義域内の任意の x, y で f(y) \geqq f(x) + \nabla f(x) \cdot (y-x) が成り立つ。これはわかる?
微分可能な凸関数の勾配が満たす条件
f が微分可能な凸関数ならば、定義域内の任意の x, y で以下が成り立つ。
f(y) \geqq f(x) + \nabla f(x) \cdot (y-x)
💜 不等式ですね……凸関数の定義と似ていますが、凸関数の定義とは少し違いますね。凸関数の定義では関数の値の方が小さいといっていましたが、その式は関数の値の方が大きいといっているようです。並べて図示すると以下でしょうか。
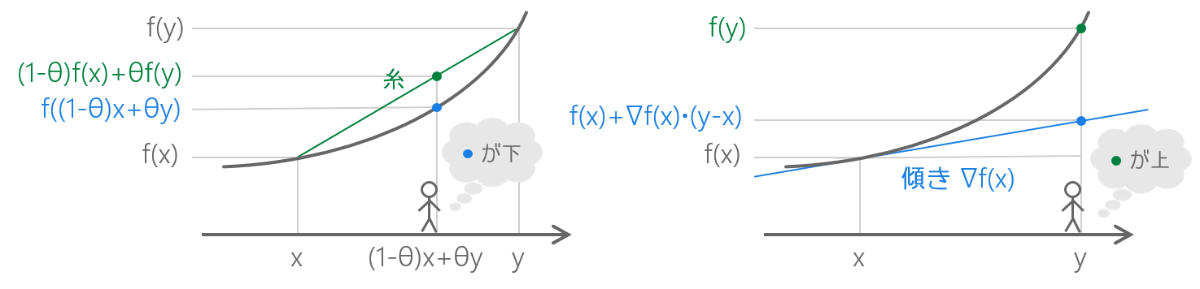
凸関数の定義(左)と微分可能な凸関数の勾配が満たす条件(右)
💜 なぜ逆になっているんでしょうか……とりあえず、f が凸関数であることの定義から出発しましょう。この式から f(x) と f(y) を引っ張り出したいです。
f( (1-\theta)x + \theta y ) \leqq (1-\theta)f(x) + \theta f(y)
\Leftrightarrow f( (1-\theta)x + \theta y ) - f(x) \leqq - \theta f(x) + \theta f(y)
両辺を \theta で割れば右辺に f(x) と f(y) が出ますね。割りましょう。以降 \theta \in (0,1] としましょう。
\displaystyle \frac{f( (1-\theta)x + \theta y ) - f(x)}{\theta} \leqq - f(x) + f(y)
\displaystyle \Leftrightarrow f(y) \geqq f(x) + \frac{f( (1-\theta)x + \theta y ) - f(x)}{\theta}
\displaystyle \Leftrightarrow f(y) \geqq f(x) + \frac{f( x + \theta(y-x) ) - f(x)}{\theta}
示したい式に寄せてみましたが……右辺第2項が微分係数の定義のような形をしていますね。微分係数の話にするために、一旦 \theta のみが変数であると考えたいです。g(\theta) \equiv f( x + \theta(y-x) ) とおきましょう。なお、f(x) が微分可能であることより g(\theta) も微分可能です。
\displaystyle \Leftrightarrow f(y) \geqq f(x) + \frac{g(0 + \theta) - g(0)}{\theta}
これを \theta \to 0 とすることにより、
\displaystyle f(y) \geqq f(x) + \left. \frac{dg(\theta)}{d\theta} \right|_{\theta = 0}
を得ます。連鎖律で g の微分を f の微分でかきましょう。以下、f の変数を x にすると最初に選んだ x と紛らわしいので f の変数を z とします。z_j(\theta) は x + \theta(y -x) の第 j 成分とします。x_j, y_j は x, y の第 j 成分とします。
\displaystyle \left. \frac{dg(\theta)}{d\theta} \right|_{\theta = 0} = \left. \frac{d z_1(\theta)}{d \theta} \right|_{\theta = 0} \left. \frac{\partial f(z)}{\partial z_1} \right|_{z = x} + \cdots + \left. \frac{d z_n(\theta)}{d \theta} \right|_{\theta = 0} \left. \frac{\partial f(z)}{\partial z_n} \right|_{z = x}
\displaystyle \qquad \qquad \; \; = (y_1 - x_1) \left. \frac{\partial f(z)}{\partial z_1} \right|_{z = x} + \cdots + (y_n - x_n) \left. \frac{\partial f(z)}{\partial z_n} \right|_{z = x}
\displaystyle \qquad \qquad \; \; = \left. \nabla f(z) \right|_{z=x} \cdot (y-x)
\displaystyle \qquad \qquad \; \; = \nabla f(x) \cdot (y-x)
これを代入することにより、f(y) \geqq f(x) +\nabla f(x) \cdot (y-x) は示されますね。示せました!
💛 そうだね。あと、凸関数の定義と比べるなら、凸関数の定義は下図の上段だけど、\theta で割ると y まで歩いたところで高さを比べていることになる(下図の中段)。さらにこの状態で \theta \to 0 とすればいま示した不等式になるよ。だから、「青の点は緑の点より下にある」っていうのは一貫しているかな。
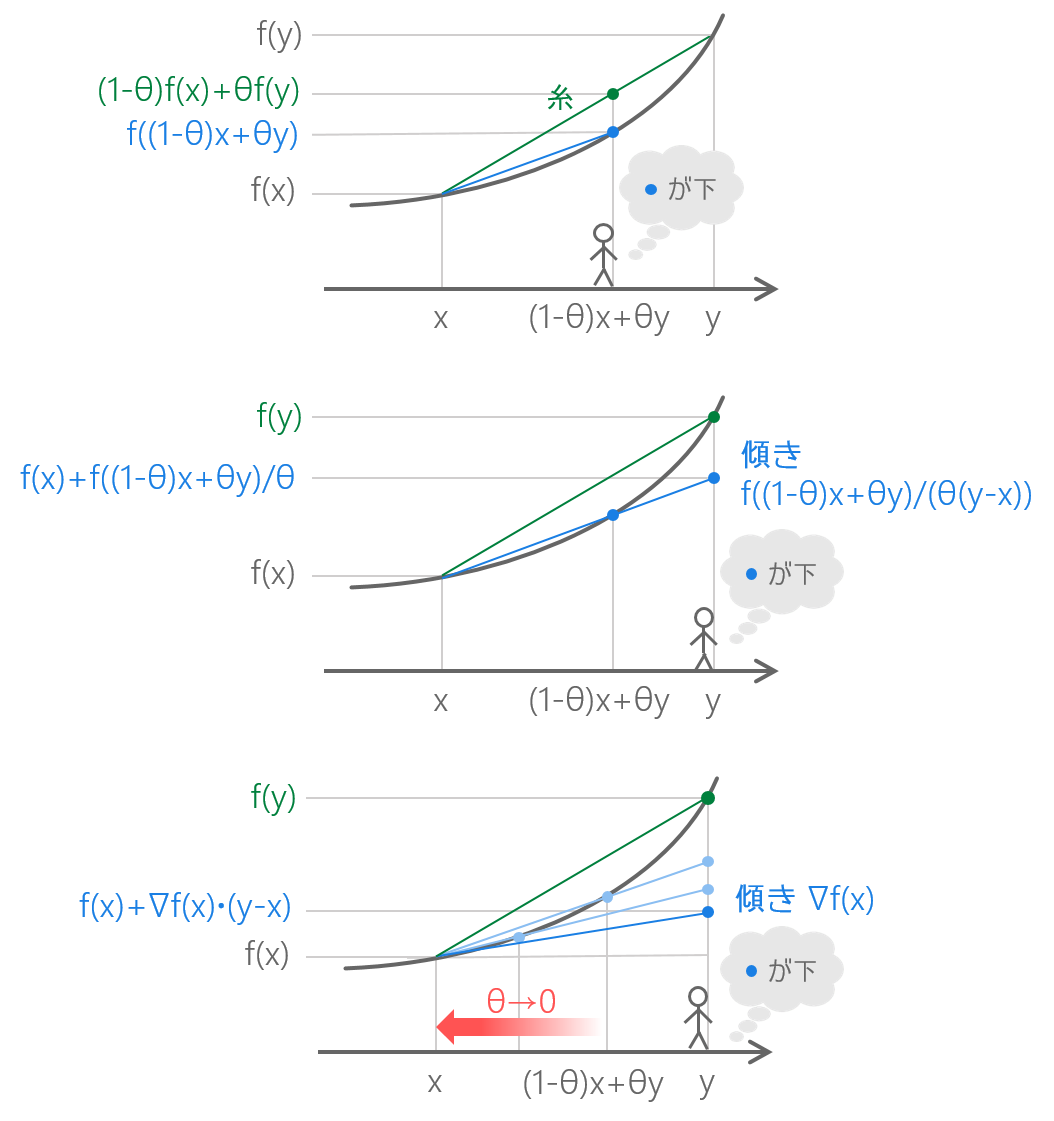
凸関数の定義が微分可能な凸関数の勾配が満たす条件になるまで
💜 あっ、確かに、ずっと青の点は緑の点より下にいますね。変わったのは2つの糸の高さを比べる場所だったんですね。
凸関数の最小点の勾配が満たす必要十分条件
💛 じゃあ次、f は微分可能な凸関数として、x^\ast が f の最小点ならば、定義域内の任意の y に対して \nabla f(x^\ast) \cdot (y-x^\ast) \geqq 0 であることはわかる?
微分可能な凸関数の最小点の必要十分条件(制約がない場合)(準備)
f が微分可能な凸関数ならば、x^\ast が f の最小点であることの必要十分条件は、定義域内の任意の y に対して \nabla f(x^\ast) \cdot (y-x^\ast) \geqq 0 であることである。
💜 えっと、まず、x^\ast が最小点であろうとなかろうと、 f(y) \geqq f(x^\ast) +\nabla f(x^\ast) \cdot (y-x^\ast) \, \Leftrightarrow \, f(y) - f(x^\ast) \geqq \nabla f(x^\ast) \cdot (y-x^\ast) が成り立つことは先ほど示しましたね。これより、任意の y に対して \nabla f(x^\ast) \cdot (y-x^\ast) \geqq 0 であれば任意の y に対して f(y) - f(x^\ast) \geqq 0 なので x^\ast は最小点です。しかし、x^\ast が最小点であれば任意の y に対して \nabla f(x^\ast) \cdot (y-x^\ast) \geqq 0 かというのは明らかではありませんね……。
💛 対偶を取ろう。\nabla f(x^\ast) \cdot (y-x^\ast) < 0 を満たす y があれば x^\ast は最小点ではないことを示そう。
💜 \nabla f(x^\ast) \cdot (y-x^\ast) < 0 なる y があった場合ですか。以下のような状況でしょうか。
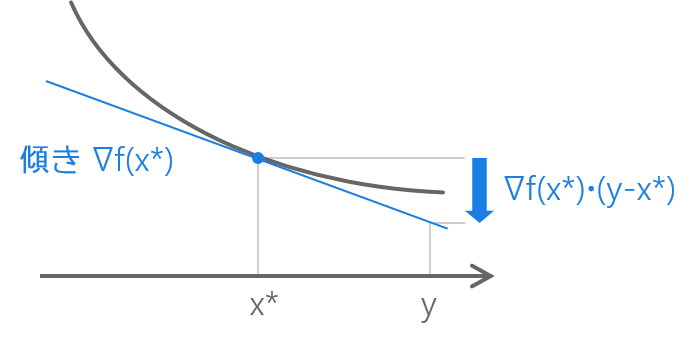
\nabla f(x^\ast) \cdot (y-x^\ast) < 0 なる y があった場合
💜 こうしてみると、x^\ast から y の向きにほんの少しだけ歩けば f の値はより小さくなりそうですね。それなら x^\ast は最小点ではないですね。\nabla f(x^\ast) \cdot (y-x^\ast) < 0 であることを利用して少しだけ歩いたところの値を得たいですが……少しだけ歩いたところ……ん?
- 先ほどは f( x + \theta(y-x) ) があって、\theta \to 0 の極限を取って \nabla f(x) \cdot (y-x) を得ましたね。
- 今回は逆です。先に \nabla f(x^\ast) \cdot (y-x^\ast) があって、とても小さい \theta の f( x^\ast + \theta(y-x^\ast) ) を知りたいのですから。
であれば……先ほど同様に、g(\theta) \equiv f( x^\ast + \theta(y-x^\ast) ) とおきましょう。x を x^\ast にかきかえただけです。\nabla f(x^\ast) \cdot (y-x^\ast) は負なので \nabla f(x^\ast) \cdot (y-x^\ast) = - \alpha \, \, \, (\alpha > 0) とおきましょう。そして先ほどの逆をたどります。
\nabla f(x^\ast)・(y-x^\ast) =-\alpha
\displaystyle \Leftrightarrow \left. \frac{dg(\theta)}{d\theta} \right|_{\theta = 0} =-\alpha
\displaystyle \Leftrightarrow \lim_{\theta \to 0} \frac{g(0 + \theta) - g(0)}{\theta} =-\alpha
\displaystyle \Leftrightarrow \lim_{\theta \to 0} \frac{f( x^\ast + \theta(y-x^\ast) ) - f( x^\ast )}{\theta} =-\alpha
そしてこの極限の意味は、任意の正数 \epsilon に対して、ある \delta が存在して、0 < |\theta| < \delta ならば
\displaystyle \left| \frac{f( x^\ast + \theta(y-x^\ast) ) - f( x^\ast )}{\theta} + \alpha \right| < \epsilon
が成り立つことでしたから、\epsilon = \alpha / 2 と取れば 0 < |\theta| < \delta_{\alpha/2} を満たす \theta で
\displaystyle -\frac{\alpha}{2} < \frac{f( x^\ast + \theta(y-x^\ast) ) - f( x^\ast )}{\theta} + \alpha < \frac{\alpha}{2}
\Rightarrow f( x^\ast + \theta(y-x^\ast) ) - f( x^\ast ) < -\alpha \theta / 2
が成り立ちます。よって x^\ast は最小点ではありません!
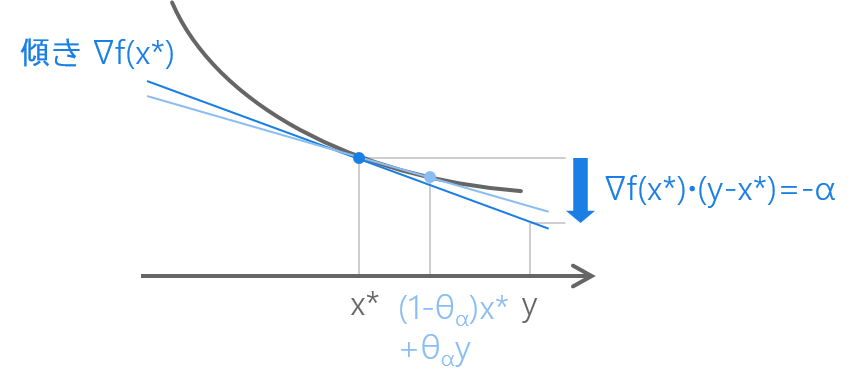
\nabla f(x^\ast) \cdot (y-x^\ast) < 0 なる y があったら x^\ast は最小点ではない(\theta_\alpha が取れる)
💛 つまり、x^\ast が最小点なら、任意の y で \nabla f(x^\ast) \cdot (y-x^\ast) \geqq 0 でなければ駄目だね。
💜 はい。それで、気付いてしまったんですが。
💛 何に?
💜 いま、\nabla f(x^\ast) \cdot (y-x^\ast) < 0 なる y があったら x^\ast は最小点ではないことを示しましたが、\nabla f(x^\ast) \cdot (y-x^\ast) > 0 なる y があったとしても x^\ast は最小点ではないですよね。\nabla f(x^\ast) \cdot (y-x^\ast) = \beta \, \, \, (\beta > 0) とおいて両辺にマイナスをかければ上の導出の要領で、 f( x^\ast + \theta(x^\ast - y) ) - f( x^\ast ) < -\beta \theta / 2 が導かれますから。逆向きにほんの少し歩けば f の値は小さくなります。
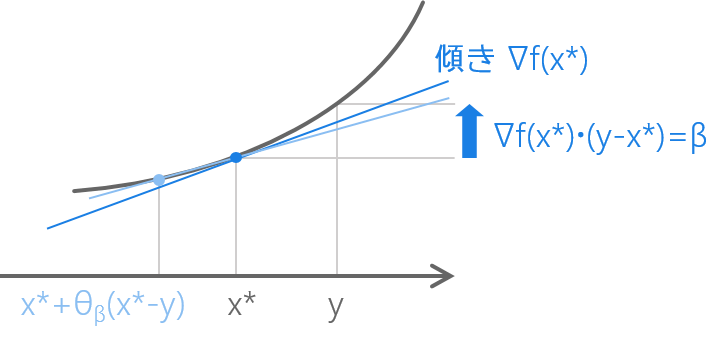
\nabla f(x^\ast) \cdot (y-x^\ast) > 0 なる y があっても x^\ast は最小点ではない(\theta_\beta が取れる)
💛 まあそうだね。いまは制約がない場合を考えているからね。
💜 制約?
(参考)制約があるときは
💛 いまは f の最小点を \mathbb{R}^n 全体から探そうと思っている。最小点を探す範囲に制約がない。でも、制約付きで考える場合もある。例えば「a \cdot x = b を満たす x の中で最小化する」みたいに。そういうとき、制約を満たす x の集合を実行可能領域というよ。
💜 はあ。その制約があったら何か変わるんですか?
💛 さっき「逆向きにほんの少し歩けば」f の値は小さくなるっていっていたけど、逆向きにほんの少し歩いたら実行可能領域からはみ出す可能性が出てくるんだよね。だったら x^\ast が最小点でないとは限らない。
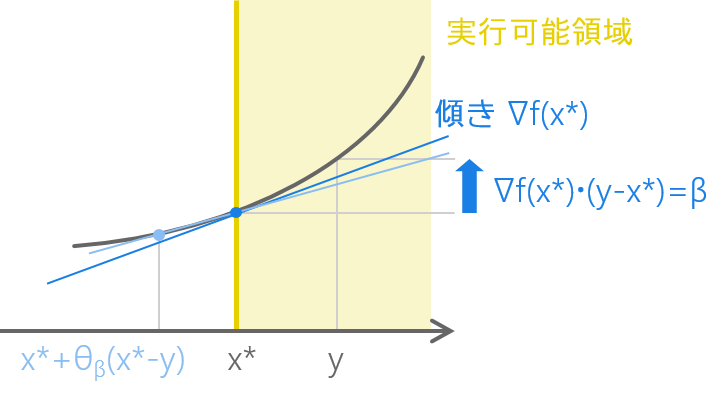
\nabla f(x^\ast) \cdot (y-x^\ast) > 0 なる y があっても制約があったら x^\ast はやっぱり最小点かもしれない
💜 ああ、そういうことですか……。いや、それをいったら \nabla f(x^\ast) \cdot (y-x^\ast) < 0 なる y があっても x^\ast は最小点かもしれないことになりませんか? x^\ast から y に少し踏み出した先が実行可能領域からはみ出ている可能性が出てくるんですよね?
💛 実行可能領域の形に何の仮定もないときはそうなっちゃうね。でも、そういうケースはこの本では扱わないかな。制約がある場合でも「凸最適化」といわれるケースのみを扱うと思うよ(テキスト名的に)。さしあたり9章は制約がないケースだからここでは詳しく説明しないけど、凸最適化は 136ページの 4.15 に定式化してある。さっきの必要十分条件を凸最適化の文脈でいうと以下かな。
最小点の必要十分条件(凸最適化の場合)
x^\ast が凸最適化の最小点であることの必要十分条件は、 実行可能領域内 の任意の y に対して \nabla f(x^\ast) \cdot (y-x^\ast) \geqq 0 であることである( f は凸最適化の目的関数)。
💛 これは x^\ast から y に少し踏み出しても実行可能領域を出ないんだ。なぜなら、凸最適化では、x^\ast と y が実行可能領域内にあれば x^\ast と y をつなぐ線分すべてが実行可能領域内に入っているから。
💜 ……ともかく、制約がある場合には最小点 x^\ast の必要十分条件は変わってくるんですね。
結局凸関数が最小になる点はどんな点
💛 そうだね。それで、最初にわからなかったことはもう解決したよね。
微分可能な凸関数の最小点の必要十分条件(制約がない場合)
f が微分可能な凸関数ならば、x^\ast が f の最小点であることの必要十分条件は \nabla f(x^\ast) = 0 。
💜 え?
💛 だって、制約がなければ下図のどちらであっても x^\ast は最小点ではないっていっていたよね。
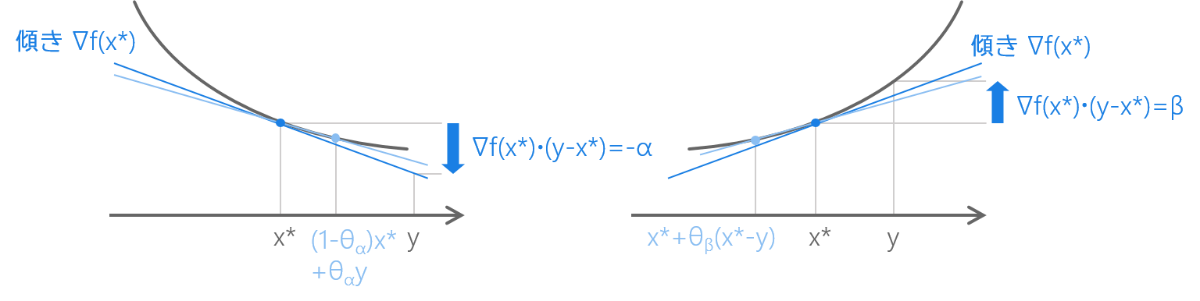
\nabla f(x^\ast) \cdot (y-x^\ast) < 0 なる y があっても \nabla f(x^\ast) \cdot (y-x^\ast) > 0 なる y があっても x^\ast は最小点ではない(より小さい値を取る点を与える \theta_\alpha や \theta_\beta が存在する)
💛 つまり、定義域内の任意の y に対して \nabla f(x^\ast) \cdot (y-x^\ast) = 0 でなければならないんだよね。なら、y = x^\ast + \nabla f(x^\ast) に対してもこれが成り立たなければならないよね。いまは制約がないからこの y がはみ出すとかはない。
💜 あ……確かに。\nabla f(x^\ast) \cdot \nabla f(x^\ast) = \| \nabla f(x^\ast) \|^2 = 0 でなければならないとなると、\nabla f(x^\ast) はゼロベクトルでなければならないですね……。
余談―だから何がうれしいのか
💛 だから \nabla f(x) = 0 であるような点 x を探しに行こう。
💜 理解しました……が、それって、「f(x) が最小になる点を探そう」を「\nabla f(x) = 0 を満たす点を探そう」にいいかえただけですよね。それで何か解決になっているんですか?
💛 逆に、「f(x) が最小になる点を探そう」っていわれてどう探すの? \mathbb{R}^n 内の点の値を全部調べるの? それで探し当てた点が最小点だってどうやっていえるの?
💜 いや、\mathbb{R}^n 内の点を全部調べるのは無理ですよ……無限にあるじゃないですか……。
💛 対して \nabla f(x) = 0 を満たす点、いいかえると、この方程式の解は、ふつう \mathbb{R}^n よりぐっと絞れるよ? 狭義凸関数だったらこういう点があるなら1点しかないし。それってかなり解決になっているよね?
💜 あ……。そうですね、「f(x) が最小になる点」では具体的にどこにあるかの手がかりになっていませんが、「\nabla f(x) = 0 を満たす点」は解けるわけですからね。具体的な方程式ですから。
💛 まあ f(x) = c(定数関数)だったら全ての点で \nabla f(x) = 0 だから何も絞り込めないんだけど、それならそれで全ての点が最小点だしね。
💜 なるほど……ある点が任意の点より小さいことを調べたくて、その情報をある点のみで調べられる条件に凝縮した結果勾配に帰着したというイメージなんでしょうか。
余談―凸関数でなかったらどうなのか
💜 そういえば、今回は最初から f が凸関数であるとされていましたけど、f が凸関数であることってどこかで使いましたっけ。
💛 十分性の証明に使ったよ。「先ほど示しましたね。これより、」のところ。
💜 ああ確かに……これって、凸関数でなかったらどうなるんですか?
💛 そのまま十分性がなくなるってだけかな。必要十分条件じゃなくて必要条件になる。
💜 というと?
💛 f が凸関数でなくても、x^\ast が最小点であってそこで f が微分可能であったら \nabla f(x^\ast) = 0 であることは変わらないよ。そっち向きの証明は微分可能性しか使っていないしね。ただ逆に、\nabla f(x^\ast) = 0 だからといって最小点とは限らなくなる。極小点や極大点の可能性が出てくるから。
💜 ああ……凸関数でなかったら極大値もあるかもしれませんし、極小値だって何箇所もあるかもしれませんね。
💛 でも、\nabla f(x^\ast) = 0 である点に候補を絞り込めばいいことは変わらないよ(制約がなければ)。最小点以外も引っかかっちゃうかもしれないってだけで。ただもし f に微分可能でない点があったらそういう点は別途確認しないといけないけどね。そういう点は \nabla f(x^\ast) = 0 ではあぶり出せないから。まあ9章では f は2回連続微分可能だからそんなことは考えなくていいけどね。
定義と主張のまとめ
凸関数の定義
f が凸関数であるとは、定義域内の任意の x, y と任意の \theta \in [0,1] に対し、以下が成り立つこと。
f( (1-\theta)x + \theta y ) \leqq (1-\theta)f(x) + \theta f(y)
微分可能な凸関数の勾配が満たす条件
f が微分可能な凸関数ならば、定義域内の任意の x, y で以下が成り立つ。
f(y) \geqq f(x) + \nabla f(x) \cdot (y-x)
微分可能な凸関数の最小点の必要十分条件(制約がない場合)(準備)
f が微分可能な凸関数ならば、x^\ast が f の最小点であることの必要十分条件は、定義域内の任意の y に対して \nabla f(x^\ast) \cdot (y-x^\ast) \geqq 0 であることである。
微分可能な凸関数の最小点の必要十分条件(制約がない場合)
f が微分可能な凸関数ならば、x^\ast が f の最小点であることの必要十分条件は \nabla f(x^\ast) = 0 。

凸関数の定義が微分可能な凸関数の勾配が満たす条件になるまで
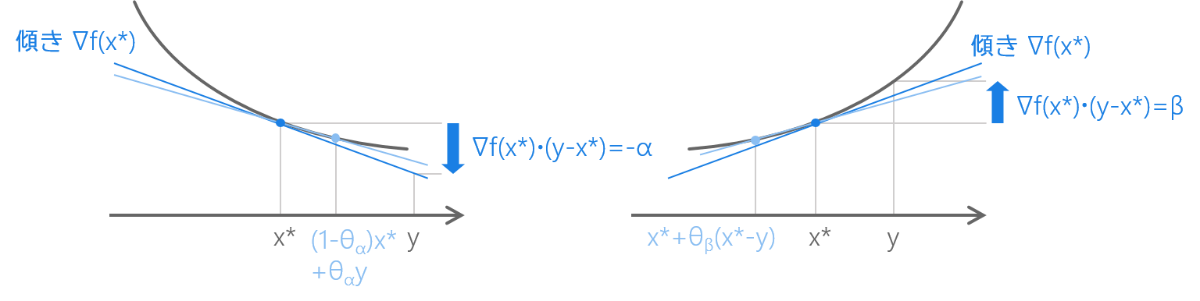
\nabla f(x^\ast) \cdot (y-x^\ast) < 0 なる y があっても \nabla f(x^\ast) \cdot (y-x^\ast) > 0 なる y があっても x^\ast は最小点ではない(より小さい値を取る点を与える \theta_\alpha や \theta_\beta が存在する)
Discussion