Bitwise演算子は何に使うの

他の言語も共通すると思いますが、今回はJSで例にします。

JSのビットワイズ演算子

演算子	ロジック	詳細
&	AND	ビットが全部1の場合のみ結果が1
|	OR	いずれのビットが1または全部が1の場合に結果が1
^	XOR	いずれかのビットが1の場合のみ結果が1（全部1の場合は0）
~	NOT	1->0, 0->1 ビット反転
<<	左シフト	二進数を左へ1桁シフトし、末尾を0で補充、左冒頭1桁が消される
>>	右シフト	左シフトの逆、末尾1桁が消される
>>>	右シフト	正数の場合は上記と同じ、マイナスの場合は符号保持

二進数のロジック演算はかなりシンプルなのでここは割愛する。

問題は、これらの演算子は一体どんな使い方ができるの？

&で偶数奇数を判断

偶数と奇数を判断するには、直感的に思い出すのは、2で割れるかどうか、ではないでしょうか。

function isEven(num: number) {
  return num % 2 === 0
}

ここで二進数の考え方でやってみると：

function isEven(num: number) {
  return num & 1 === 0
}

理由についてですが、まずはいくつか例をみた方がわかりやすい：

0 => 0000
1 => 0001
2 => 0010
3 => 0011
4 => 0100
5 => 0101
6 => 0110
7 => 0111
8 => 1000
9 => 1001

これで気づくかもしれませんが、奇数の場合、一番右側は必ず1だということです。当たり前のことですが、AND 1で計算すると、1以外は全部0埋めで結果は0となり、一番右の1桁のみで判断がつきます。

&で剰余取得

一部の言語ではModulo演算となっていますが、JSではremainder(剰余)しかないのです。ただ、厳密に言えば ModuloとRemainderは違います（詳細はこちら）

いずれにしても、プラスの整数だけを想定して、次のようにANDを使うことが可能：

  13 %    4 =    1   （13 を 4 で割った余りは 1 に等しい）
1101 & 0011 = 0001   （2**2 - 1 = 3 => 0011）

ビットワイズの操作は通常の%よりパフォーマンスが良いらしい（こちら）ですが、ここでいくつかの制限があります。

• プラスの整数を想定
• 剰余の対象（4）は、2のn冪となるのが条件
• &演算に切り替える時、2**n - 1 => 3

うん。。これで実用性が微妙かな、と言っても、ハッシュ関数での応用ができます。例えば配列のサイズを2**nにしておくと、ハッシュ関数で% lengthより、& length - 1を使うことで、この処理のスピードを向上できるらしい。

|と&でフラグオンオフをチェック

wikipedia先生から教えてもらった実用ケースがありますが、その例で、4つのフラグは1000, 0100, 0010, 0001で想定して良いでしょう。すると|を使ってまとめて渡すことが可能で、処理時はまた&で該当ビットが1/0かを判断。

実際にJSとかでも使われているかというと、答えはYES。

Reactのソースコードには割と見当たります。例えばこちらのフックエフェクトタグのファイルですが、上記の例と同じ考えで、違うビットの1/0でフラグを表示しています。

export type HookEffectTag = number;

export const NoEffect = /*             */ 0b00000000;
export const UnmountSnapshot = /*      */ 0b00000010;
export const UnmountMutation = /*      */ 0b00000100;
export const MountMutation = /*        */ 0b00001000;
export const UnmountLayout = /*        */ 0b00010000;
export const MountLayout = /*          */ 0b00100000;
export const MountPassive = /*         */ 0b01000000;
export const UnmountPassive = /*       */ 0b10000000;

それで運用もほぼ一緒です（こちら）。

import {
  NoEffect as NoHookEffect,
  UnmountSnapshot,
  UnmountMutation,
  MountMutation,
  UnmountLayout,
  MountLayout,
  UnmountPassive,
  MountPassive,
} from './ReactHookEffectTags';
// ...
function commitHookEffectList(
  unmountTag: number,
  mountTag: number,
  finishedWork: Fiber,
) {
  // ...
  if (lastEffect !== null) {
    const firstEffect = lastEffect.next;
    let effect = firstEffect;
    do {
      if ((effect.tag & unmountTag) !== NoHookEffect) { 
        // Unmount
        // ,,,
      }
      if ((effect.tag & mountTag) !== NoHookEffect) {
        // Mount
        // ...
      }
      effect = effect.next;
    } while (effect !== firstEffect);
  }
}

ビットワイズがreactでどう使われているかについて、こちらとこちらも参照。

^で値の一致をチェック

かつて、「算術演算子(arithmetic operator)を使わずにaとbの値が一致かどうか」の問題を出会ったことがあります。

当時はビットワイズ演算の知識がなく、「何アホなこと言ってんの」のが感想でした。

^演算の結果は以下となります。

0 ^ 0 = 0
1 ^ 0 = 1
0 ^ 1 = 1
1 ^ 1 = 0

この結果を言い換えれば、ビット（1/0）が一致する場合、結果が必ず0となる、となります。そのため：

function isEqual(a: number, b: number) {
  return a ^ b === 0
}

function areEqual(nums: number[]) {
  const res = nums.reduce((acc, cur) => {
    acc ^= cur
    return acc
  }, 0)
  return res === 0
}

で、数字が同じかどうかをチェックできます。

^で変数値の入れ替え

^演算にはもう一つ面白い使い方があります。

Pythonには、変数の値を入れ替えたい時に、一行で書くことができます。これはunpackingの一種ですが、詳しくはこちらにまとめています。

x = 10
y = 15

x, y = y, x

jsでは、少し書き方を変える必要があります。

[x, y] = [y, x]

また、XOR演算を利用すれば、temp変数を作らずに交換することも可能：

x = 2
y = 3

x = x ^ y
y = x ^ y
x = x ^ y // x = 3, y = 2

何が起こっているかというと：

0010 ^ 0011 => 0001 // x = 1, y = 3
0001 ^ 0011 => 0010 // x = 1, y = 2
0001 ^ 0010 => 0011 // x = 3, y = 2

ただ、これは数字にしか聞かないので、実際使用時に使うかどうかは微妙かもしれません。

~で-1をブールに変換

例えば配列からある要素を探そうとしています。findとかindexOfとか使えると思いますが、indexOfで見つからなかった場合-1が返ってきます。これを~演算で変換すると：

~-1 = 0

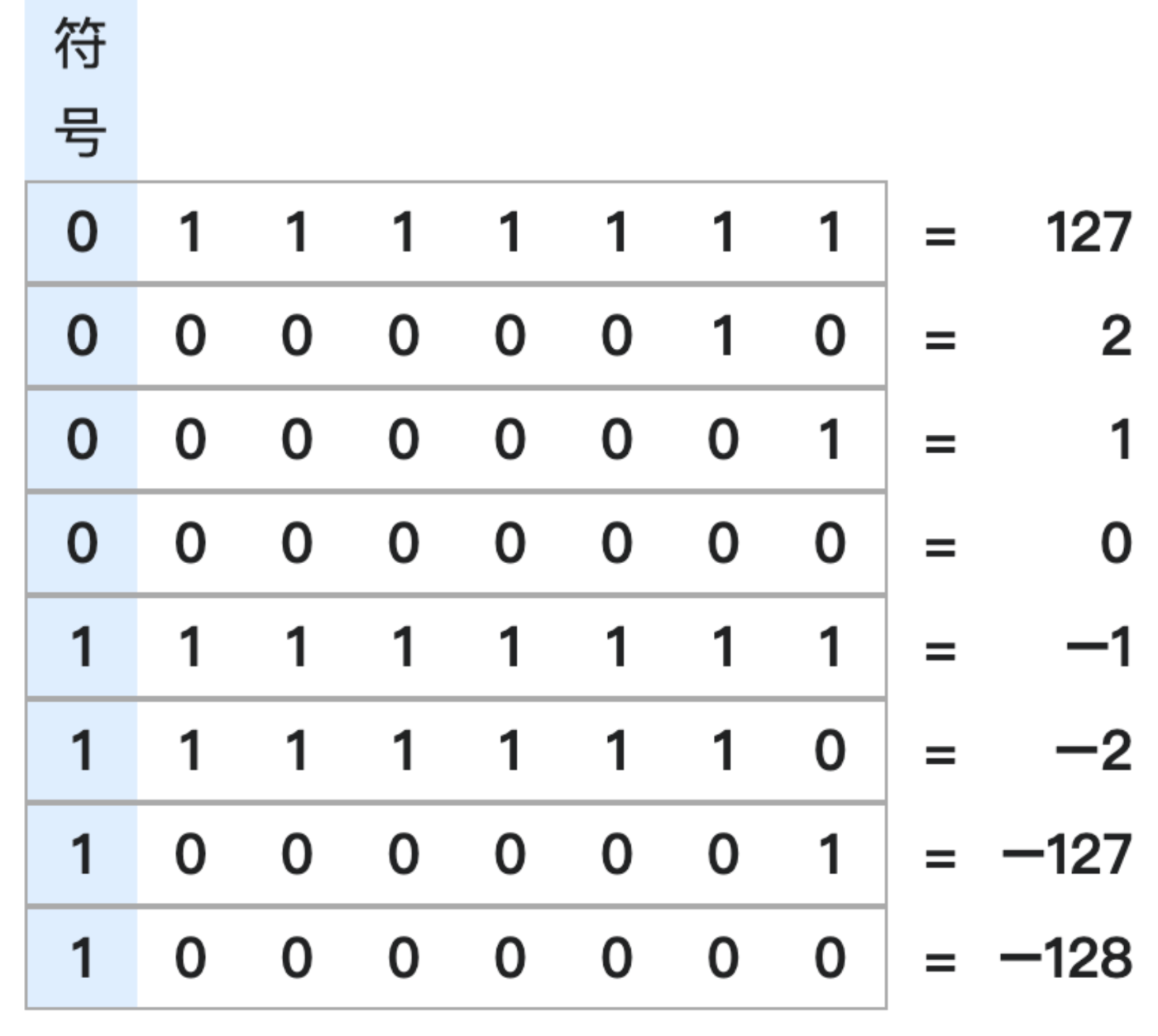
理由について、 例えば32ビットの符号あり整数（signed int）で見ると、一番左のビットは±を表示するビットとなります。マイナスの場合は、そのビットが1となり、プラスの場合は0となります。0はすべてのビットが0となりますが、~演算ですべてのビット反転することとなります。

// ~0 = -1
0  => 00000000000000000000000000000000 
-1 => 11111111111111111111111111111111

逆に言えば、-1にNOT演算すると、0に戻ります。すると：

function isFound(index) {
  return !!(~index)
}
isFound(arr.indexOf(...)) // true / false

ちょっと待って、なぜ-1のバイナリーが11111...11になるの？？

これは2の補数（complement）と言います。二進数でマイナス数字を表すときに利用されます。計算方法は：

A - B = A + (-B) = A + not(B) + 1

- B = not(B) + 1

となります。例えば、Bが5の場合、二進数では0101=>not(B) = 1010=>not(B)+1 = 1011となります。それで0001も同じやり方で計算すると、1111となるのです。

ビットシフト

<<と>>で、全体的にビットを左または右へ移動させることですが、実際に使う場面はあるかな。

>>と>>>の違いといえば、先ほど±の符号のビットの話がありましたが、それと関係あります。>>>の方は、符号がどうであれ、必ず0が一番左から入ってきます。0となるとプラスになるので、>>>は必ずプラスの数字をリターンすることです。ただ、>>はマイナス数字の場合、符号をキープするために、0ではなく1を左側から入れてきます。例えば：

//  170 => 00000000000000000000000010101010
// -170 => 11111111111111111111111101010110
// 170 >> 3
// --------------------------------------------
//    (***)00000000000000000000000010101(010)
// --------------------------------------------
//  = (000)00000000000000000000000010101(***)
// --------------------------------------------
//  = 00000000000000000000000000010101
// --------------------------------------------
//  = 21 (decimal)
// -170 >> 3
// --------------------------------------------
//    (***)11111111111111111111111101010(110)
// --------------------------------------------
//  = (111)11111111111111111111111101010(***)
// --------------------------------------------
//  = 11111111111111111111111111101010
// --------------------------------------------
//  = -22 (decimal)
// -170 >>> 3
// --------------------------------------------
//    (***)11111111111111111111111101010(110)
// --------------------------------------------
//  = (000)11111111111111111111111101010(***)
// --------------------------------------------
//  = 00011111111111111111111111101010
// --------------------------------------------
//  = 536870890 (decimal)

console.log(170 >> 3); // 21
console.log(-170 >> 3); // -22
console.log(-170 >>> 3); // 536870890

つまり、数字がプラスもしくは0の場合、どれを使っても同じですが、マイナスになると使い分けが必要です。

話に戻しますが、ビットシフトは計算上どういう意味があるかというと、1ビットを移動する度に、2を掛けるまたは2で割ることを意味します。なので：

1 << 3 // 1 * 3**2 = 9
2 >> 1 // 2 / 2**1 = 1
5 >> 2 // 5 / 2**2 = 1

しかも、これで整数が戻るので、小数を整数へ変換することが不要です。例えばバイナリーサーチ(二分探索)の場合、中心点を探すときにこう書けます：

function search(nums, target) {
  let l = 0, r = nums.length - 1
  while (l <= r) {
    let mid =  (r + l) >> 1
    // let mid =  l + Math.floor((r - l) / 2)
    if (nums[mid] == target) {
      return mid
    } else if (nums[mid] > target) {
      r = mid - 1
    } else {
      l = mid + 1
    } 
  }
  return -1
}

ビットワイズで操作する場合、10進数に戻すときの数値がオーバーフローしてしまうことがなくなるので、Math.floor((l+r)/2)よりは安全かつシンプルな書き方となります。

終わりに

ビットワイズの日常的に実用的になりそうな使い方を調べてみましたが、やはり分野によってだいぶ変わる気がします。例えば圧縮、暗号化のアゴリズムではかなり依存しているらしいです。ウェブ開発になるとあまり使わないかも、とのイメージがありますが、実際にreactとかでも普通に使われています。なのでソースを読むためにも、CSの基礎のためにも、ビットワイズは学んで損はないでしょう。

ではでは。