連結リストのちょっとした問題集
やれやれ、最近転職して色々と忙しかったのですが、一ヶ月ほど何も書いていなかったとは。
ということで今回何かネタになるものを書こうかなと思ったところ、面接の準備で色々とleetcodeをやっていたので、少しまとめとして書こうと思います。前回では木とグラフでしたが、今回は少し近くてよりシンプルなデータ構造、連結リスト(link list)にします。
連結リストの概要
前回の記事で少し触れましたが、メモリでの保存方法から見れば、連結リストは木、グラフと同じく、メモリーのユニットで値と次のユニットのメモリーアドレスを指すポインターの情報が保存されています。そのため、探索するときは配列のような連続メモリーを使うケースと違い、O(1)のランダムアクセスができず、基本的にO(n)の時間複雑度になります。
また、配列ともう一つ大きな違いというのは、配列で要素を挿入、削除するときに、連続しているメモリーを使っているため、挿入・削除インデックス以降のデータのシフトコストがかかります。例えば、配列の冒頭(index=0)にデータを挿入しようとすると、全てのデータを1ずつずらす必要があります。この操作がO(n)となってしまいます。それに対して、連結リストではポインターの指すメモリーアドレスを変えれば良いので、O(1)で操作可能となります。
| 操作 | 配列 | 連結リスト |
|---|---|---|
| 探索 | O(1) | O(n) |
| 挿入 | O(n) | O(1) |
| 削除 | O(n) | O(1) |
連結リストには主に2種類あります。
- 単方向連結リスト(singly linked list)、一方通行となり、現時点のノードに置いて前のノードを知ることができません。
- 双方向連結リスト(doubly linked list)、名前通り双方向トラバースが可能となるため、現時点のノードにおいて前のノードと次のノードを知ることができます。ただもう一つのポインターを保存する分、メモリー使用量が単方向より増えます。その代わりに、O(1)の時間複雑度で任意のノードの前のノードを取得できるので、一部のケースで挿入、削除操作が単方向より効率がよくなります。
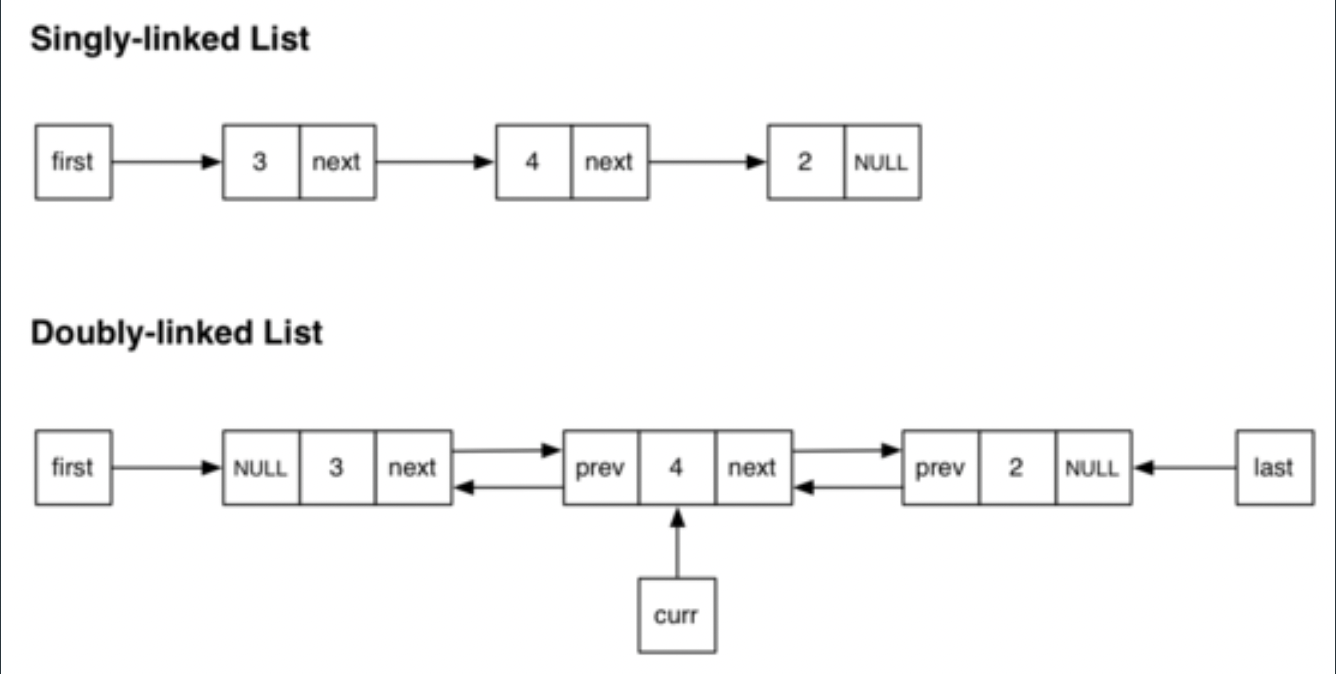
コードで見るとprevポインターが存在するかどうかの違いになります。
class SingleNode {
constructor (val, next) {
this.val = val || 0
this.next = next || null
}
}
class DoubleNode {
constructor (val, next, prev) {
this.val = val || 0
this.next = next || null
this.prev = prev || null
}
}
ここまで見て少し違和感があるかもしれません。連結リストの挿入と削除操作はすでにO(1)で可能となりますが、双方向にすることで何が「効率良い」のか、そもそもO(1)はもう良くする余地ないのではないか、とのところです。
ここはもう少し詳しく説明すると、例えば削除操作のところで、2つのパターンが存在します。
- 値がわかり、その値と等しいノードを削除する
- メモリーアドレスがわかり、そのアドレスにあるノードを削除する
パターン1に関しては、単方向にしても双方向にしても特に変わりがありません。指定値のノードを探すためにO(n)がかかります。パターン2の場合は、単方向だともう一度探索して、prevとなるノードを探す必要がありますが、双方向の場合は不要となります。このパターンになると、O(n)からO(1)とレベルアップするのです。
単方向連結リストにはサイクルが存在する特別なパターン(circular linked list)があります。基本構造は同じですが、最後のノードのnextがnullではなく、最初のノードを指すことになります。サイクル存在判定の問題はよく見られますので、また実例のところで詳しく見たいと思います。
上記の種類の連結リスト以外に、RedisのSorted Setを実現しているスキップリスト(skip list)といった少し改造されたデータ構造もありますが、今回は割愛します。興味のある方は こちら に参照してください。
実践がすべて
理論的な話はここまでとして、早速問題を見ながら説明しようと思います。
回文連結リスト
初見の試み
こちらの 234. Palindrome Linked List 問題となります。
この問題を解く前に、「回文(Palindrome)」とは何か、先に押さえた方が良いでしょう。簡単にいえば、読み順を逆にしても同じ結果になるデータシーケンスのことです。例えば、1221, abcbaなど。もちろん日本語にも存在します( こちら )。
もしフォローアップの条件を無視すると、確かにシンプルにアゴリズムが思い浮かぶのではないでしょうか。
- 空の配列を作る
- 連結リストをheadから探索
- 値を配列にプッシュ
- 配列を双方向から探索し(ツーポインター)、値が同じかどうかをチェック
この方法ではO(n) time & O(n) spaceで解決可能です。悪いアゴリズムではありません。もし面接とかであったら、全然アリだと思います。
フォローアップ条件でチャレンジ
この問題の難易度はなんとeasyとなっていますが、これはあくまでも目安です。というのは、もしfollow upのO(n) time & O(1) spaceの条件だと、easyとは考えにくいでしょう。
では、O(1) spaceの条件をクリアするにはどうすれば良いでしょうか。
連結リストの問題で、O(1) spaceを見たときに、別途メモリーを使うことができないので、ポインター操作が必要との方向で考えるのはほぼ間違いありません。となると、どう操作すれば、この問題のコアに接近できるのか。
この問題は「回文」を判断するのが目的になります。回文判断には、通常ツーポインター(two pointers)を使うのが多いですが、探索の方法には大体2つのパターンがあります。
- 二つのポインターを用意し、中心から両端へ探索
- 二つのポインターを用意し、両端から中心へ探索
違いというのは、中心から両端へ探索するときに、文字数が奇数か偶数かのケースを考慮する必要があります。例えば、abbaとabcbaを見れば、abbaの厳密的な「中心」が存在しないので、二つのポインターが別々の場所からスタートすることになりますが、abcbaの場合は、二つのポインターがcからスタートすることになります。両端から中心へ探索する時に、奇数と偶数の考慮が不要になります。もちろん、二つのパターンにはそれぞれの利用ケースがあるので、一概にどれが良いとはいえません。
いずれにしても、「中心」と「両端」というキーワードが掴みました。どの方向にしても、探索可能にするために、連結リストの半分のポインター方向を反転する必要があります。つまり:
1 -> 2 -> 3 -> 2 -> 1 を
-
1 <- 2 <- 3 -> 2 -> 1にするか - もしくは
1 -> 2 -> 3 <- 2 <- 1にするか
どのパターンにするかはさておき、ここでもう一つ問題が出てきました。中心となるノードをどうすれば見つけられるのだろうか。
ツーポインターのテクニックはよく配列や連結リストの問題に使われます。有限なリストに「中心」を探すには、fast/slowのポインターを利用し、fastが2を進み、slowが1を進むことで、fastが終点にたどり着いたら、slowが「中心」にあるはず、とのことです。ただ、ここにも偶数と奇数のケースがあるので、偶数の場合にピッタリとする「中心」がないので、注意が必要です。
ここまで考えると、中心を探すとか、連結リストを反転するとか、いずれも要素個数が偶数奇数の問題があるので、ここで一旦両端から中心へ探索の案にしたら、少しやりやすくなるかもしれません。
となると、アゴリズムを整理すると:
- fast/slowのツーポインターで連結リストの中心を見つける
- 後ろ半分の連結リストを反転する
- 両端から中心へツーポインターで探索し始める
- 違う値となれば回文ではない、探索が終了となれば回文であると判定できる
では、コーディング(こちら)に:
/**
* Definition for singly-linked list.
* function ListNode(val, next) {
* this.val = (val===undefined ? 0 : val)
* this.next = (next===undefined ? null : next)
* }
*/
/**
* @param {ListNode} head
* @return {boolean}
*/
var isPalindrome = function(head) {
/* 1. fast/slowのツーポインターで連結リストの中心を見つける */
let slow = head, fast = head
// 終了条件に要注意、fastが毎回2ステップ進むので、fast !== nullかつfast.next !== nullとなっています
while (fast && fast.next) {
fast = fast.next.next
slow = slow.next
}
// このタイミングで、slowが中心に位置する
/* 2. 後ろ半分の連結リストを反転する */
// 反転するときにnextを別のノードに指すことが必要ですが、初めてのノードにはターゲットがないので、
// ここでダミーとなるprevをnullとして定義
let prev = null
// slowを中心から終点まで探索するため、終了条件はslow !== nullとなります
while (slow !== null) {
let next = slow.next // 古いnextを見失わないように先に保存
slow.next = prev // 新しいnextをprevに指定
prev = slow // prevを現在のノードに更新
slow = next // 現在のノードを古いnextに指定
}
// この時点で slow = null, prev が終点に位置する
// ここまで行くと
// 1 -> 2 -> 2 ->1 が 1 -> 2 -> 2 <- 1 になりますが、
// 事実上2つの連結リストを意味ます : 左の1 -> 2 -> 2 -> null と右の 1 -> 2 -> null
// 同様に、 1 -> 2 -> 3 -> 2 -> 1 が 1 -> 2 -> 3 <- 2 <- 1 となり、
// 2つの連結リストが同じく 1 -> 2 -> 3 -> null
// 奇数と偶数のケースの違いがあると忘れずに
/* 3. 両端から中心へツーポインターで探索し始める */
// 左のポインターはheadのままでOKで、右はslowではなくprevとなります
let left = head, right = prev
// 終了条件は偶数奇数の違いにより、leftではなく、rightで判断する必要があります
while (right !== null) {
if (left.val !== right.val) {
/* 4. 違う値となれば回文ではない */
return false
}
left = left.next
right = right.next
}
/* 4. 探索が終了となれば回文であると判定できる */
return true
};
この問題でカバーされているテクニックといえば:
- 連結リストの探索
- 連結リストの反転
- ダミーノードでエッジケースを対応
- ツーポインター(slow/fast, 両端から中心)
があります。いずれも連結リスト問題によく見られるテクニックなので、この問題が個人的にライクにしています。
フロイドのカメとウサギ
概要の節では、サイクルが存在する連結リストについて少し触れました。先ほどの問題では、slow/fastポインターのテクニックで中心点を探すことができました。これ以外に、連結リストのサイクル判定に利用することができます。ここでその問題を少し見てみたいと思います。
141. Linked List Cycle と 142. Linked List Cycle II がほぼ同じなので、直接142に行きます。
141では単にサイクル存在するかどうかの判断ですが、アゴリズムは割と単純です。
- fast/slowポインターを使い、headノードから探索
-
fast === null || fast.next === nullであれば、サイクルがない -
slow === fastとなったタイミングで、サイクルがあるとの判断
ただ、142ではそのサイクルの始まりのノードを見つけ出すことが必要です。fast/slowを使うのが分かったのですが、始まりのノードをどのように見つけ出せるのかが問題になります。
もしサイクルが存在する場合、fastポインターがslowと会うまでに、サイクルの部分にクルクル回ることが想像できます。二つのポインターが会うノードと、サイクルの始まりのノードとは違う可能性がありますが、一定の距離dを空いていると仮定しましょう。fastがslowより常に二倍速で進むので、会う時にslowが移動した距離(ノード数)がkであれば、fastが2kとなります。図にすれば、何かわかるようになるのではないでしょうか。
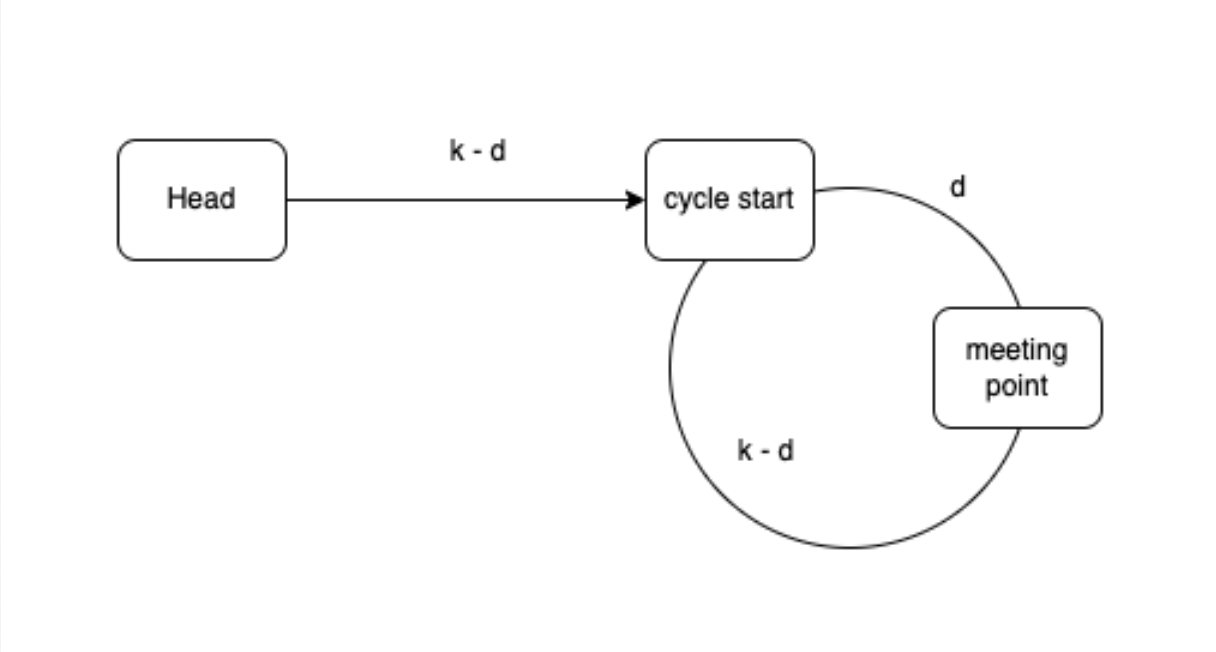
slowがkの距離を移動したため、連結リストのheadノードからサイクルのスタートノードまでの距離はk-dとなるはずです。また、fastが2k移動したため、円周も2k - k = kのはずです。となれば、2つのポインターが合うノードから、k-d の距離を移動すれば、始まりのノードに戻ると推測できます。つまり、headからk-dの距離を移動し、同時にmeeting nodeからk-dの距離を移動すれば、二つのポインターがstart nodeで合流するはずです。
なるほど、であればアゴリズムを整理すると:
- fast/slowポインターを使い、headノードから探索
-
slow === fastとなったタイミングで、サイクルがあるとの判断できる -
fast === null || fast.next === nullであれば、サイクルがないため、ここはnullをリターン -
slow/fastポインターのいずれかからポインターを移動、同時にheadからのポインターも移動、slow/fast === headのタイミングでサイクルのスタートノードとなる
では、コーディングに:
/**
* Definition for singly-linked list.
* function ListNode(val) {
* this.val = val;
* this.next = null;
* }
*/
/**
* @param {ListNode} head
* @return {ListNode}
*/
var detectCycle = function(head) {
// 1. fast/slowポインターを使い、headノードから探索
let slow = head, fast = head
while (fast && fast.next) {
slow = slow.next
fast = fast.next.next
// 2. `slow === fast`となったタイミングで、サイクルがあるとの判断できる
if (slow === fast) {
break
}
}
// 3. サイクルがないため、ここはnullをリターン
if (fast === null || fast.next === null) {
return null
}
// 4. slowをheadへ戻し、fastと一緒に移動
slow = head
// サイクルが存在すると確証があるため、二つのポインターが合うまでループ
while (slow !== fast) {
slow = slow.next
fast = fast.next
}
return slow // この時点でslow/fastがサイクルのスタートノードに位置する
}
このアゴリズムは、 Robert W. Floyd によって考案されていたため(彼ではないとの異論もあり)、フロイドアゴリズム(floyd algorithm)とも呼ばれています。 グラフの最短経路問題にも彼の名で命名されるアゴリズムがありますが、このサイクル検知とは別です。slow/fastポインターの応用ケースによく例としてあげられる問題だと思います。
反転と再帰
最後に連結リストの反転について、少し違うやり方を見てみたいと思います。
206. Reverse Linked List の方がイージーで、92. Reverse Linked List II がミディアムとなります。問題は難しい方92を貼りますが、206の問題はleft=1,right=nという、92の特殊なケースとなります。

全部反転する時に、先ほどの問題ではwhileループを使うやり方がすでにわかりました。ここで再帰のやり方で考えてみます。
連結リスト全体の反転
再帰は関数のやることを定義し、ベースケースまで関数内で呼び出す形が基本です。例えば206の連結リスト全体を反転する場合、任意のノードにおいて、そのノードのnextを同じ関数に渡して実行し、nextがnullとなれば(ベースケース)リターンするのが考えられます。
function reverseLinkList(head) {
// ベースケース
if (!head || !head.next) {
return head
}
// 今のノードのnext以降のノードに対して再帰実行
// リターン値は最後のノードとなり、反転後のheadノードでもあります
let lastNode = reverseLinkList(head.next)
// 今のノードの次の次のノードを自分に指定し、nextをnullに指定
head.next.next = head
head.next = null
return lastNode
}
head.next.next = head のところが少しわかりにくいかもしれません。実際に1 -> 2 -> 3を例で見れば、1にとってのnextが2、反転すると2のnextが1となるので、1のnext.nextが自分に指すことになります。head.next = nullによって、連結のポインターnextを破棄にしています。再帰の呼び出しはこれらの操作の前になるので、head.next.nextによって正しい反転後のnextに繋ぐことができます。例えばhead=2の時に、2のnextがここでnullとなりますが、実行順番的に、head=1の時点で1へ指すように正しくセットされます。もしこの辺りが分かりにくいのであれば一度1 -> 2 -> 3の例で手書きでも書いたらすぐにわかるでしょう。
少しレベルアップ
206番の問題では、連結リストを初めから終わりまで全て反転するようになっています。92番の問題では、leftとrightを指定した区間のノードを反転する、が必要なので、それに到達するにはもう少し工夫が必要です。ただ、先ほども述べましたが、206番の問題をleft = 1, right = nだと考えても構いません。ここで、少し難易度を下げて、left = 1, right = k (k <= n)のケースを考えてみましょう。つまり、連結リストのk番目のノードまで反転することです。
k番目までとなると、先ほどの206と何が違うのだろうか。考え方が基本的に同じですが、一番大きな違いといえば、206の場合、反転によって始まりのheadノードのnextがnullになりますが、部分的に反転すると、headノードのnextがnullではなく、k+1番目のノードになるはずです。なので、headからk+1番目のノードへうまく繋ぐように少しコードを変更しなければなりません。
let nextNode = null
function reverseToK(head, k) {
// ベースケース
if (k === 1) {
// この時点でhead=k番目のノードなので、k+1番目のノードをnextNodeとして保存
// 1 -> 2 -> 3 -> 4 k = 3を例にすれば、k=1となれば、head=3, nextNode = 4
nextNode = head.next
return head
}
// 今のノードのnext以降のノードに対して再帰実行
// リターン値は最後のノードとなり、反転後のheadノードでもあります
let lastNode = reverseToK(head.next, k-1)
// 今のノードの次の次のノードを自分に指定し、nextをnextNodeに指定
head.next.next = head
head.next = nextNode
return lastNode
}
実行順番的に、再帰呼び出しが反転操作より先なので、コールスタックではまずベースケースまで行きます。そこでnextNodeを指定します。head.next = nextNodeで、全てのノードのnextがk+1番目のノードになるのではないの?との疑問があるかもしれません。206のところにも触れましたが、実行順番で言えば、次のhead.next.next = headのところで訂正されるので問題ありません。
例:1 -> 2 -> 3 -> 4, k = 3
-> 1層目始まり head = 1, k = 3
lastNode = rev(head.next, k-1)
-> 2層目始まり head = 2, k = 2
lastNode = rev(head.next, k-1)
-> 3層目始まり head = 3, k = 1
nextNode = head.next = 4
return head
-> 2層目へ戻る
lastNode = 3層目リターン値 = 3
head.next.next = head = 2
head.next = nextNode = 4 => このタイミングでは間違い
return lastNode
-> 1層目へ戻る
lastNode = 2層目リターン値 = 3
head.next.next = head = 1 => ここで訂正される
head.next = nextNode = 4
ただ、実際に再帰の問題を考えるときに、上記のようにコールスタックを書き出す必要がありません。繰り返しになりますが、現時点のノードにおいて、何をするかだけを考えれば良いことです。head=1の時点で言えば、head.next = nextNodeの操作では、nextNodeがk+1番目のノードを指すことが必要です。また、再帰呼び出しの場所によって、実行順番の違いについて少し感覚を掴むとより理解しやすくなります(前回の木・グラフの記事にも参照)。
連結リスト一部の反転
だいぶ近づいています。結局、92番の問題と比べて、leftが変数か1かの違いになっています。そのため、left = 1がベースケースだと考えて、そこでreverseToKを呼び出すことが考えられます。先ほどの関数を利用しながら、もう一層の再帰をすれば解決できます。
function reverseBetween(head, left, right) {
// ベースケースではreverseToKを呼び出す
if (left === 1) {
return reverseToK(head, right)
}
head.next = reverseBetween(head.next, left-1, right-1)
return head
}
ここで少しトリッキーなところというのは、head.next = reverseBetween(head.next, left-1, right-1)の再帰です。leftから反転することということは、始まりのheadノードにとってleft個の距離があるとの解釈でも可能です。すると、head.nextノードにとって、left-1個の距離となります。これを続けていくと、いずれleft-1-1-1...-1 = 1となるのです。なので、ここの再帰呼び出しがやっているのは、反転するスタートノードを位置調整することだけです。これで92番が解決できます。
終わりに
今回は連結リストについていくつかの問題の解け方、よく使われるテクニックについてまとめてみました。基礎知識だけが分かっても、初見でこれらも問題を解こうとすると、やはりチャレンジングなことになります。特にフロイドアゴリズムについて、研究者が歳月を掛けて練り出した発想を面接の環境で独自考案できる人は天才の中の天才としか思えません。
そのため、結局コーディングテストを制覇するには、練習が成敗を決めます。もちろん、ひたすら解こうとするよりも、問題の種類と回答のテクニックが分かった上で練習すると、より効果的になるに違いないでしょう。
ではでは。
Discussion