Housnerの近似式

自由表面を有する矩形水槽において、加速度応答による変動水圧分布の算定式のうちの一つである、Housnerの近似式について、導出過程を日本語で概要をまとめたWeb記事がなかったので備忘録として残します。

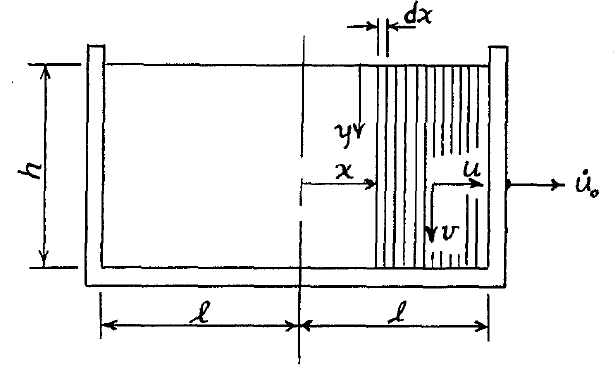
衝撃圧

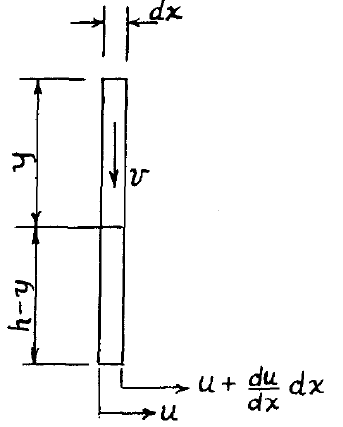
側壁にある加速度を与えると、上図の微小区間に拘束される流体の垂直方向の速度は、

$$v=(h−y)dudx v = (h-y)\frac{du}{dx}$$

非圧縮性流体のとき、加速度は同様に下式を満たす。

$$v˙=(h−y)du˙dx \dot{v} = (h-y)\frac{d\dot{u}}{dx}$$

流体の密度を $ρ\rho$ とすると、流体中の圧力は下式で求められる。

$$∂p∂y=−ρv˙ \frac{\partial p}{\partial y} = - \rho \dot{v}$$

側壁に作用する水平方向の力の総和は次のようになる。

$$P=∫0hp dy P = \int_0^h p \, dy$$

これらの式を変形すると下式のように書ける。

$$v˙=(h−y)du˙dxp=−ρ∫0y(h−y)du˙dxdy=−ρh2(y/h−12(y/h2))du˙dxP=−ρh2∫0y(y/h−12(y/h)2)du˙dxdy=ρh3/3du˙dx \begin{align} \dot{v} &= (h-y) \frac{d \dot{u}}{dx} \\ p &= - \rho \int_0^y (h-y) \frac{d\dot{u}}{dx} dy = - \rho h^2 \left(y/h - \frac{1}{2}(y/h^2) \right) \frac{d \dot{u}}{dx} \\ P &= -\rho h^2 \int_0^y \left(y/h - \frac{1}{2}(y/h)^2 \right) \frac{d \dot{u}}{dx} dy = \rho h^3 / 3 \frac{d\dot{u}}{dx} \end{align}$$

加速度 $u˙\dot{u}$ は、2枚の膜の間に含まれる流体の水平方向の動きから決定され、微小区間の左右２つの面の圧力が異なれば、x方向に加速されることになる。
運動方程式は、

$$dPdx=−ρh dx u˙ \frac{dP}{dx} = - \rho h \, dx \, \dot{u}$$

$PP$ について代入して変形すると、

$$d2u˙dx2−3h2u˙=0 \begin{align} \frac{d^2 \dot{u}}{dx^2} - \frac{3}{h^2}\dot{u} = 0 \end{align}$$

$u˙\dot{u}$の一般解は、

$$u˙=C1 cosh3 xh+C2 sinh3 xh \begin{align} \dot{u} = C_1 \, \text{cosh} \sqrt{3} \, \frac{x}{h} + C_2 \, \text{sinh} \sqrt{3} \, \frac{x}{h} \end{align}$$

矩形水槽に作用する変動水圧

矩形水槽では、境界条件は $x=±lx = \pm l$ のとき、$u˙=u0˙\dot{u} = \dot{u_0}$となる。
このとき、

$$u0˙=C1 cosh3 lh+C2 sinh3 lhu0˙=C1 cosh3 −lh+C2 sinh3 −lh=C1 cosh3 lh−C2 sinh3 lh \begin{align} \dot{u_0} &= C_1 \, \text{cosh} \sqrt{3} \, \frac{l}{h} + C_2 \, \text{sinh} \sqrt{3} \, \frac{l}{h} \\ \dot{u_0} &= C_1 \, \text{cosh} \sqrt{3} \, \frac{-l}{h} + C_2 \, \text{sinh} \sqrt{3} \, \frac{-l}{h} = C_1 \, \text{cosh} \sqrt{3} \, \frac{l}{h} - C_2 \, \text{sinh} \sqrt{3} \, \frac{l}{h} \end{align}$$

よって、

$$C1=u0˙cosh3lhC2=0 \begin{align} C_1 &= \frac{\dot{u_0}}{\text{cosh}\sqrt{3}\frac{l}{h}} \\ C_2 &= 0 \end{align}$$

したがって、矩形水槽の場合の加速度 $u˙\dot{u}$ は、

$$u˙=u0˙cosh3xhcosh3lh \dot{u} = \dot{u_0} \frac{\text{cosh}\sqrt{3}\frac{x}{h}}{\text{cosh}\sqrt{3}\frac{l}{h}}$$

となる。また、圧力に関する式は次のようになる。

$$p=−ρu0˙h3(y/h−12(y/h)2)sinh3xhcosh3lhP=−ρu0˙h23sinh3xhcosh3lh \begin{align} p &= - \rho \dot{u_0} h \sqrt{3} \left(y/h - \frac{1}{2}(y/h)^2 \right) \frac{\text{sinh}\sqrt{3}\frac{x}{h}}{\text{cosh}\sqrt{3}\frac{l}{h}} \\ P &= - \rho \dot{u_0} \frac{h^2}{3} \frac{\text{sinh}\sqrt{3}\frac{x}{h}}{\text{cosh}\sqrt{3}\frac{l}{h}} \end{align}$$

側壁に働く変動水圧は、符号に注意すると $x=lx=l$ のとき、

$$pw=ρu0˙h3(y/h−12(y/h)2) tanh3lh p_w = \rho \dot{u_0} h \sqrt{3} \left(y/h - \frac{1}{2}(y/h)^2 \right) \,\text{tanh}\sqrt{3}\frac{l}{h}$$

底壁に働く変動水圧は、 $y=hy=h$ のとき、

$$pw=ρu0˙h32 sinh3xhcosh3lh p_w = \rho \dot{u_0} h \frac{\sqrt{3}}{2} \,\frac{\text{sinh}\sqrt{3}\frac{x}{h}}{\text{cosh}\sqrt{3}\frac{l}{h}}$$

参考文献

• 『円筒貯槽の地震入力』　河野和間ら
• 『FRP構造の設計基準とその事例』　邉 吾一
• THE DYNAMIC BEHAVIOR OF WATER TANKS, G. W. Housner.
• DYNAMIC PRESSURE ON ACCELERATED FLUID CONTAINERS, G. W. Housner.