実装から始めるはじめての強化学習
どうもこんにちは。
積読した書籍が700冊を突破しました、connectome.design のアプリケーションエンジニアの康です。
最近では、会社の Zenn ブログに記事を書く機会を得られたため、ようやく長らく積んでいた強化学習の書籍に手を伸ばし、初歩的な勉強を始めました。
この記事では、強化学習の実装に重点を置き、解決する問題を極力単純化にして、強化学習に対しての理解を深めたいと考えております。
はじめに
強化学習は、機械学習の手法の一つであり、目的である収益の最大化を達成するため、状態に応じて適切な行動を選択する方策(Policy)を求めています。
その中にも、複数の手法がありますが、ここでは強化学習の手法の一つである、 Q 学習を利用し、実際に問題を解かせてみました。
そして、今回の問題は用意した数列に含む数字を推測させることです。内容は以下になります。
- 事前に数列の要素である数字の範囲を決める。
例:1 ~ 3 - 事前に決めた範囲の数字で数列を作成する。
例:3, 1, 2, 1 - 数列の一つ目の数字から、順番ごとに一つずつ数字を当てさせ、正解か不正解かを回答する。
- 正解を当てた場合、その次の数字を当てさせ、不正解になった場合、最初からやり直す。
例:数列の一つ目の数字は 1 と当てる。不正解であるため、もう一度当てさせる。
例:数列の一つ目の数字から、3 → 1 → 3 と当てる。三つ目の数字が不正解であるため、最初からやり直す。
例:数列の一つ目の数字から、3 → 1 → 2 → 1 と当てる。すべて正解であるため、成功とみなす。
こちらの問題に関して、最終的に数列に含むすべての数字を順番通りに推測させることを目標としています。
備考:こちらの問題は至極単純で、実際に強化学習を使用するまでもなく、総当たりで効率的に数列の数字を求めることができます。
実装
今回の強化学習の実装は、主にエージェント(Agent)と環境(Environment)の二つに分かれています。
エージェントは、実際に行動を実行し、最適化するための方策を求めています。
環境は、エージェントの行動を受け、適切なフィードバックを提供し、実行した後の状態や報酬などをエージェントに与えています。
最初に、今回の主役である、Q 学習のエージェントの実装から見ていきます。
実際に作成した以下のソースコードは、書籍「ゼロから作るDeep Learning ❹ ―強化学習編」と「Pythonで学ぶ強化学習 : 入門から実践まで」の二冊を参考して作成したものです。
import math
from collections import defaultdict
import numpy as np
class StepResult:
def __init__(self, state, reward, is_done):
self.state = state
self.reward = reward
self.is_done = is_done
class IEnvironment:
def reset(self) -> StepResult:
pass
def step(self) -> StepResult:
pass
class QLearningAgent:
def __init__(self, env: IEnvironment, actions, gamma=1, alpha=0.9, epsilon=0.01):
self._env = env
self._actions = actions
self._gamma = gamma
self._alpha = alpha
self._epsilon = epsilon
self._Q = defaultdict(lambda: 0)
self._action_to_action_index_dict = {}
for index, action in enumerate(actions):
self._action_to_action_index_dict[action] = index
def _get_action(self, state):
action_size = len(self._actions)
if np.random.rand() < self._epsilon:
action_index = np.random.choice(range(action_size))
return self._actions[action_index]
qs = [self._Q[(state, action_index)] for action_index in range(action_size)]
max_action_index = np.argmax(qs)
return self._actions[max_action_index]
def _update(self, state, action, reward, next_state, is_done):
action_index = self._action_to_action_index_dict[action]
action_size = len(self._actions)
if is_done:
next_q_max = 0
else:
next_qs = [self._Q[next_state, act_index] for act_index in range(action_size)]
next_q_max = max(next_qs)
target = reward + self._gamma * next_q_max
self._Q[state, action_index] += (target - self._Q[state, action_index]) * self._alpha
def learn(self, episodes):
reward_history = []
max_reward_history = []
max_total_reward = -math.inf
for episode in range(1, episodes + 1):
state = self._env.reset()
total_reward = 0
while True:
action = self._get_action(state=state)
step_result = self._env.step(action)
next_state = step_result.state
self._update(
state=state,
action=action,
reward=step_result.reward,
next_state=next_state,
is_done=step_result.is_done,
)
total_reward += step_result.reward
if step_result.is_done:
break
state = next_state
reward_history.append(total_reward)
max_total_reward = max(total_reward, max_total_reward)
max_reward_history.append(max_total_reward)
if episode > 0 and episode % 10000 == 0:
print(f"Episode: {episode}, Maximum Total Reward: {max_total_reward}")
return reward_history, max_reward_history
def play(self):
original_epsilon = self._epsilon
# 探索せず、利益を最大化する行動のみを選択
self._epsilon = 0
actions = []
state = self._env.reset()
while True:
action = self._get_action(state=state)
actions.append(action)
step_result = self._env.step(action)
if step_result.is_done:
break
state = step_result.state
# epsilon を元の値に戻す
self._epsilon = original_epsilon
return actions
StepResult は単純なラッパークラスで、IEnvironment はエージェントに利用させるための環境に必要なものを定義したインターフェースです。
エージェントの QLearningAgent に関して、以下のメソッドが存在しています。
-
_get_action:状態によって、次の行動を決める役割を担っています。
1 - ε の確率で、最大価値をもたらす行動を最新の Q 関数(行動価値関数)から選択することになりますが、残りの ε の確率で、すべての行動からランダムで一つを選択することになります。(ε = 0 の場合、常に最大価値をもたらす行動を選択するようになります。) -
_update:ベルマン最適方程式を使用し、状態/行動/報酬等の値で計算して、Q 関数(行動価値関数)を更新する。
-
learn:指定したエピソード数で、環境に対して学習して、Q 関数を更新する。(学習した際のエピソードごとの収益などの履歴も取得する)
-
play:現時点の Q 関数を利用し、計算上最大収益をもたらす行動を環境に対して実行する。(実行した行動履歴も取得する)
そして、解かせる問題の環境(Environment)の実装は、以下になります。
import math
from agent import IEnvironment, StepResult
class GuessSequenceNumber(IEnvironment):
def __init__(self, numerical_sequence: list[int], lower_boundary=math.inf, upper_bonddary=-math.inf):
super()
min_number = min(min(numerical_sequence), lower_boundary)
max_number = max(max(numerical_sequence), upper_bonddary)
self._guessable_numbers = list(range(min_number, max_number + 1))
self._solution = numerical_sequence
self._guessed_count = 0
self._corrected_guess_score = 1
self._incorrect_guess_score = -1
def reset(self) -> StepResult:
self._guessed_count = 0
return self._guessed_count
def step(self, guessed_number) -> StepResult:
assert 0 <= self._guessed_count < len(self._solution), "Game is ended. Please using reset function to restart."
if guessed_number != self._solution[self._guessed_count]:
self._guessed_count = -1
return StepResult(state=self._guessed_count, reward=self._incorrect_guess_score, is_done=True)
self._guessed_count += 1
# 全て正解した場合、終了する
is_done = self._guessed_count == len(self._solution)
return StepResult(state=self._guessed_count, reward=self._corrected_guess_score, is_done=is_done)
def get_guessable_numbers(self):
return self._guessable_numbers
環境の GuessSequenceNumber について、以下のメソッドが存在しています。
- reset:環境を初期化する(初期状態 = 0)。
- step:数列の数字を当てる。
当てれる数字は、状態に依存しています。
状態 = 0 の場合、1つ目の数字を当てれる。状態 = 1 の場合、2つ目の数字を当てれる。
その際、当てる数字と実際が異なる場合、ペナルティとして、報酬を -1 にして、数字当てを強制終了する。
当てる数字が正解である場合、報酬 1 を付与し、次の数字を当てる(状態 + 1)。ただし、次の数字がない場合、すべての数字が正しいであるため、数字当てを終了する。 - get_guessable_numbers:事前に決めていた範囲の中で、数列に含まれる可能性があり、当てれるすべての数字候補。
最後に、すべてを動かすメインの実装は以下になります。
import matplotlib.pyplot as plt
import numpy as np
from agent import QLearningAgent
from guess_sequence_number import GuessSequenceNumber
if __name__ == "__main__":
episodes = 50
numerical_sequence = [1, 3, 3, 2, 2, 1, 3, 3, 3, 1, 2, 3, 1, 1, 1]
env = GuessSequenceNumber(numerical_sequence=numerical_sequence, lower_boundary=1, upper_bonddary=3)
agent = QLearningAgent(env, actions=env.get_guessable_numbers())
reward_history, max_reward_history = agent.learn(episodes=episodes)
actions = agent.play()
fig, axs = plt.subplots(3)
axs[0].plot(range(1, len(reward_history) + 1), reward_history, "o")
axs[0].set_xlabel("Episode")
axs[0].set_ylabel("Total Reward")
axs[1].plot(range(1, len(max_reward_history) + 1), max_reward_history)
axs[1].set_xlabel("Episode")
axs[1].set_ylabel("Maximum Total Reward")
axs[2].plot(range(1, len(actions) + 1), actions, "o")
axs[2].set_xlabel("Order of Action")
axs[2].set_ylabel("Action")
axs[2].set_xticks(np.arange(0, 16, 1))
fig.tight_layout()
plt.show()
こちらについて、最初に答えである数列の情報を定義しています。
用意した数列は、1, 2, 3 の数字を使用して、15 個の要素で作成したものです。
1, 3, 3, 2, 2, 1, 3, 3, 3, 1, 2, 3, 1, 1, 1
その後、環境及びエージェントを生成し、学習させ、実際に推測する。
最後に、その実行結果をグラフに出力しています。
結果
実際に学習させた結果は、以下になります。
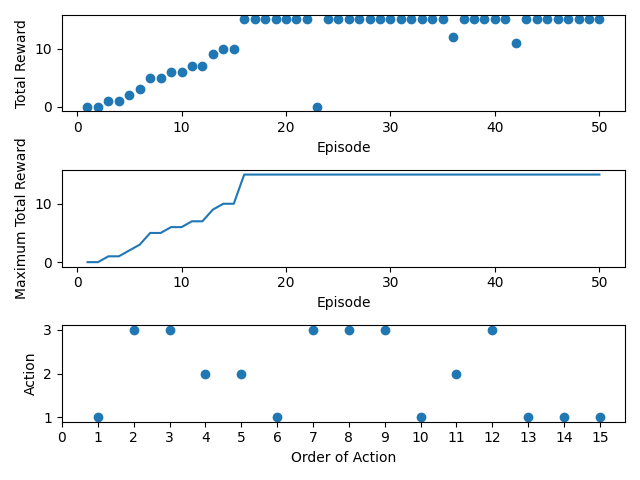
今回の数列当ては、Q 学習で学習させた結果、20 エピソードくらいで最大収益(全ての数字を当てること)にたどり着きました。
指定していた 50 エピソードまでにも、ε = 0.01 の確率でランダムに行動を変更することで、ほかに最大収益が存在するかどうかを探索することが、エピソードごとの合計収益から推察することができました。
そして、学習済みの Q 関数に従って、最大収益をもたらす一連の行動(数字当て)は、三つ目のグラフから確認することができます。
エージェントが実行した行動(Action)とその順番は、以下になります。
1 → 3 → 3 → 2 → 2 → 1 → 3 → 3 → 3 → 1 → 2 → 3 → 1 → 1 → 1
こちらについて、事前に用意していた数列の値と一致していたため、強化学習で正しく数列の値を推測して、行動を再現することができました。
おわりに
今回は強化学習の中にある Q 学習を利用して、数列の数字を推測させていました。
このような単純な問題設定は学習の一歩としてよいかもしれませんが、現実世界の問題を解決するには、まだまだ距離があります。
このギャップを埋めるためには、今後より複雑な問題や、深層学習を取り入れた深層強化学習などを勉強することが必要かもしれません。
参考資料
斎藤康毅. ゼロから作るDeep Learning ❹ ―強化学習編. 東京: オライリー・ジャパン; 2022.
隆宏久保. Pythonで学ぶ強化学習 : 入門から実践まで. 2nd ed. 東京: 講談社; 2019.
杉山聡. 本質を捉えたデータ分析のための分析モデル入門 : 統計モデル、深層学習、強化学習等用途・特徴から原理まで一気通貫!. 東京: ソシム; 2022.
AIcia Solid Project. 強化学習の探検. YouTube. [Online]. Available: https://www.youtube.com/playlist?list=PLhDAH9aTfnxI1OywfnxXCDTWGtYL2NxJR
Discussion