Vertex AI Workbench を使ってデータの傾向を統計分析で把握する

はじめに

こんにちは、クラウドエース データ ML ディビジョン所属の中村です。
クラウドエースの IT エンジニアリングを担うシステム開発部の中で、特にデータ基盤構築・分析基盤構築からデータ分析までを含む一貫したデータ課題の解決を専門とするのがデータ ML ディビジョンです。

本記事では BigQuery および VertexAI Workbench（Python3.10）を使って、データセットの傾向を把握する流れを記載します。
データ分析の参考になれば幸いです。

VertexAI　Workbench とは

Google Cloud のプロダクト、VertexAI Workbench について少しご説明します。
VertexAI は Google Cloud の提供する AI や機械学習のプラットフォームです。
本記事で使用する VertexAI Workbench は Jupyter Notebook を使用して、コードの実行を行うことができるプロダクトです。
BigQuery と簡単に連携できるため、データのクエリやモデルの開発に向いています。
詳しくは公式ドキュメントをご覧ください。

実行環境を作成する

インスタンス作成

まずは Workbench でインスタンスを作成します。

1. VertexAI Workbench を開き、「新規作成」を押します
   

2. 「詳細オプション」を押します
   
   インスタンスの詳細設定が開きます。
   必要に応じてノートブック名を変更します。

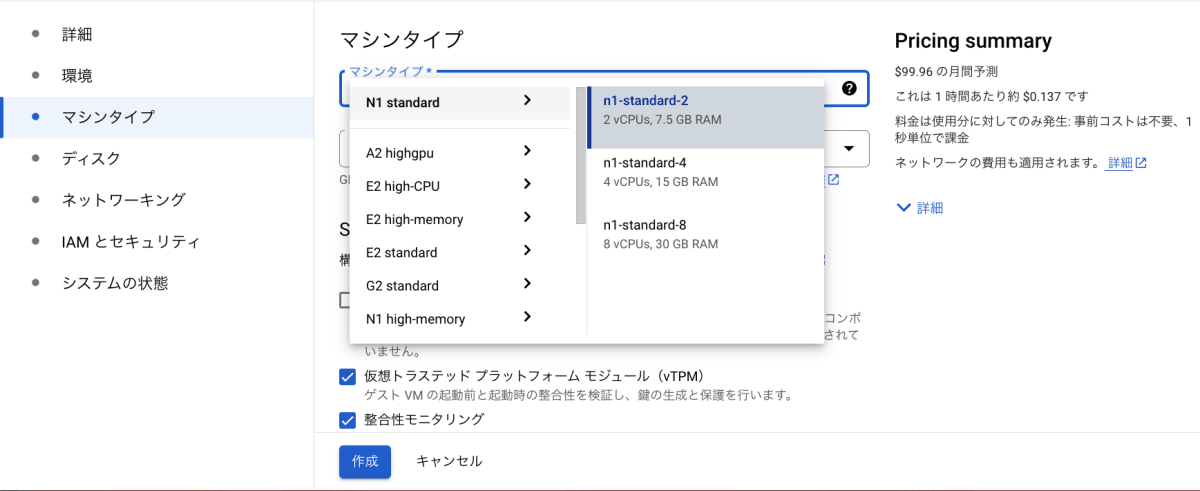
3. 「マシンタイプ」の中から「n1-standard-2」を選択します
   今回はハイスペックなメモリや CPU は必要ないので、低料金の「n1-standard-2」を使用します。
   マシンタイプごとの料金の詳細については公式ドキュメントをご確認ください。
   

4. 「作成」を押します
   少し待つとインスタンスが作成されます。
   

環境構築

Workbench 環境の初期の Python バージョンは3.7.12ですが、少し古いため Python3.10 を使えるようにします。

1. インスタンスの「JUPYTERLABを開く」を押します
   

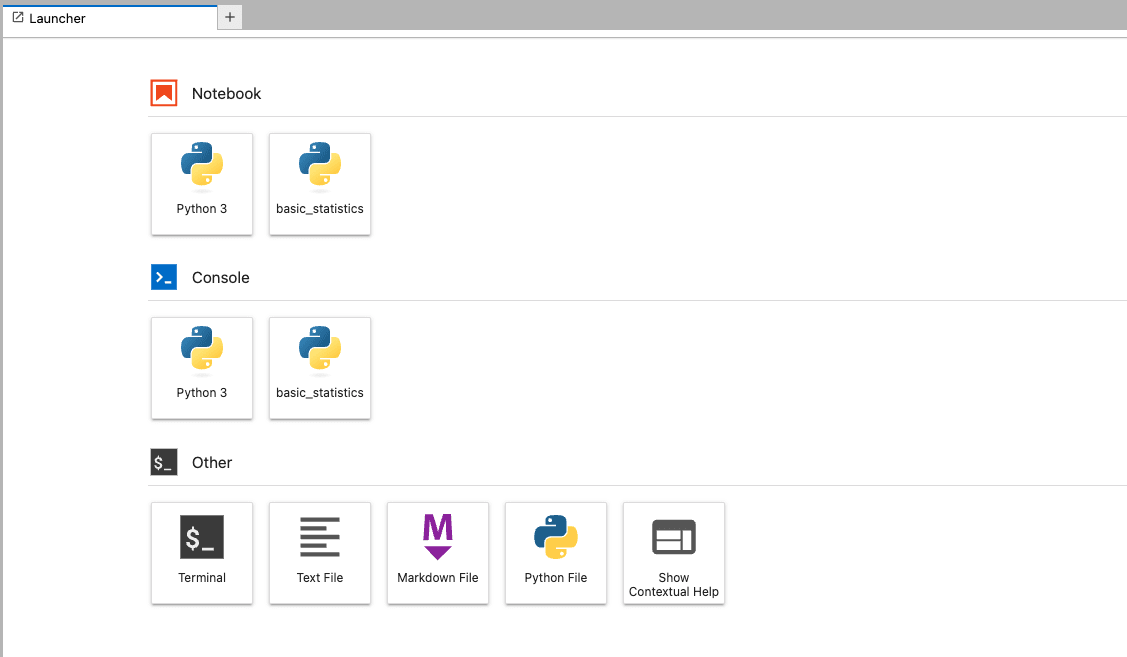
2. ターミナルを開きます
   

3. 以下のコマンドで Python3.10 の環境をcondaで作成します

conda create -n basic_statistics python=3.10

4. 3の環境を有効にします

conda activate basic_statistics

5. ipykernel をインストールします

pip install ipykernel

6. 記事で使用するライブラリをインストールします

pip install pandas matplotlib japanize_matplotlib scikit-learn seaborn google-api-python-client db-dtypes google-cloud-bigquery==2.34.1 google-cloud-bigquery-storage==2.22.0 

7. 3の環境が Jupyter Notebook で認識されるように設定します

ipython kernel install --name "basic_statistics" --user

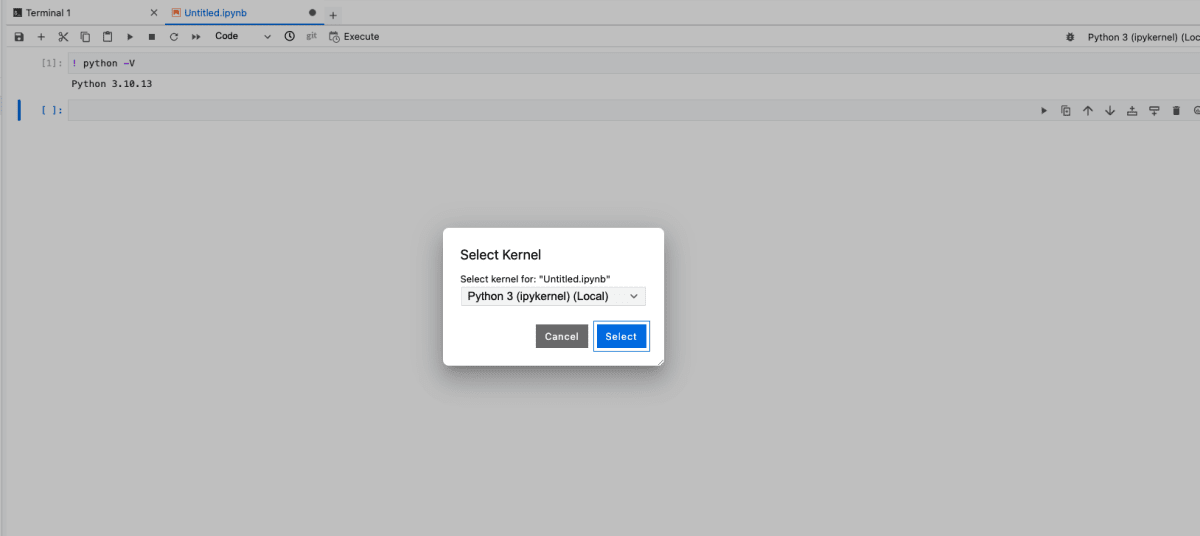
8. ページをリロードすると、jupyter notebook の右上のカーネルで「ipykernel」(basic_statistics 環境)が認識できるようになります。
   

以降のコードは、「basic_statistics」の環境で実行します。
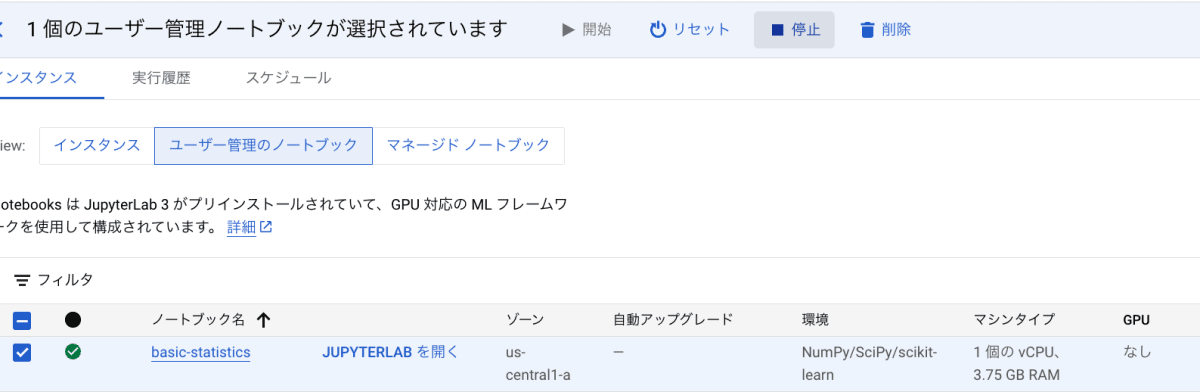
なお、インスタンスが稼働している間は課金されますので、使い終わったらインスタンス停止もしくは削除してください。

単一のデータセットの傾向を見る

データの傾向を掴むためには、平均値や中央値、最頻値などの単一の値を求めるだけでは不十分です。
というのも、それらの値が同じであってもデータの分布の仕方が異なる場合があるためです。

データの分布を見ることで、データ固有の特徴や傾向を掴むことができます。
この章では、単一のデータセットの傾向を知るときによく利用される、度数分布表とヒストグラムについてみていきます。
BigQuery のデータをWorkbenchで利用するので、連携の手軽さにもご注目ください。

題材

e-Statというサイトをご存知でしょうか。
政府統計のデータがまとまっていて、検索や表示ができる便利なサイトです。
今回はこの e-Stat から、2022年の貯蓄現在高，貯蓄・負債現在高の差額階級別世帯分布>二人以上の世帯・勤労者世帯の統計のうち、勤労世帯の貯蓄現在高データ（以降貯蓄データと表記）を題材として使っていきます。

データ準備

以下の手順で、データの準備および CSV を BigQuery へ格納します。

1. データの整形
   題材の貯蓄データをダウンロードします。
   フォーマットを元データから変更し、画像のように階級の以上・未満と度数がわかりやすい形に整形して CSV で保存します。
   

2. BigQueryを開く
   コンソール画面の左上のメニューから「BigQuery」を選択します。
   

3. データセット作成画面を開く
   プロジェクト名の右の三点リーダーをクリックし、「データセットを作成」を選択します。
   

4. データセットを作成する
   データセット名は適宜変更してください。
   ロケーションはリージョンに設定します。
   

5. テーブル作成画面を開く
   作成したデータセット名の右の三点リーダーをクリックし、「テーブルを作成」を選択します。
   

6. テーブルを作成する
   画像のように設定します（データセット名は4で作成したものです）。
   「ファイルを選択」では、1で作成した CSV を指定してください。
   設定完了後、「テーブルを作成」ボタンを押します。
   
   
   

7. 確認
   テーブルが作成されていることを確認します。
   

BigQuery と Workbench の連携について

BigQueryのデータをWorkbenchで使うにはいくつか方法があります。
本記事では、マジックコマンド %%bigqueryを利用しています。
マジックコマンド %%bigqueryを使用するとセル内でクエリし、その結果をDataFrameとして利用できます。
そのため、WorkbenchではBigQueryの必要なデータのみをクエリし、分析に使用することができます。
今回使用するデータは少量ですが、より大規模なデータでも同様にBigQueryのデータをWorkbenchで分析することができます。

BigQueryとWorkbenchのプロジェクトが別の場合や、IAMで制限をかけている場合は認証が必要です。
認証方法についてはこちらをご確認ください。

度数分布表

度数分布表を作ることで、一つの図にそのデータの特徴を集約させることができます。
今回はまず、全勤労世帯の世帯別貯蓄データをもとに度数分布表を作成してみます。

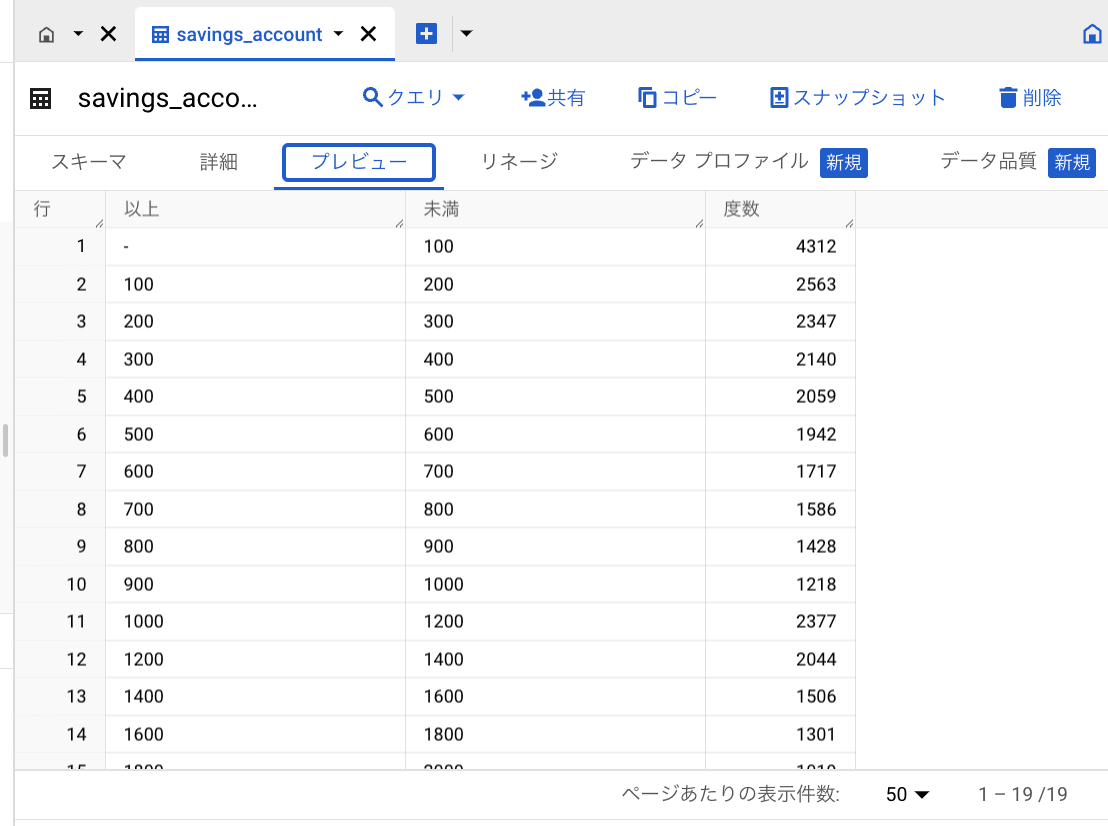
データ準備で用意した BigQuery のテーブルから、度数分布表を求めていきます。

import pandas as pd
import os
from typing import List

# BigQueryのテーブルを読み出す
%%bigquery df
SELECT
  *
FROM
  `{project_id}.dataset.savings_account`

def calc_class_value(df:pd.DataFrame)->List[int]:
    """階級値を計算する

    Args:
        df (pd.DataFrame): 度数分布表を求めたいデータ

    Returns:
        List[str]: 階級値のリスト
    """
    # 最初と最後の階級の以上・未満を仮定する
    df["以上"][0] = 0
    new_miman = df["以上"].iloc[-1]+df["未満"].iloc[-2]-df["以上"].iloc[-2]
    df.loc[df.index[-1], "未満"] = new_miman

    class_values =[(df["未満"][i] + df["以上"][i])/2 for i in range(len(df))]
    return class_values

def calc_relative_frequency(frequency,mode)->float:
    """相対度数を計算する

    Args:
        frequency (int): 度数
        mode (str): frequency:相対度数 / accumulation:累積相対度数

    Returns:
        float: 相対度数
    """
    if mode=="frequency":
        total_frequency = sum(list(frequency))
    if mode=="accumulation":
        total_frequency = list(frequency)[-1]
    relative_frequency = [i/total_frequency for i in frequency]
    return relative_frequency

if __name__ == "__main__":
    # 階級の単位
    class_unit = "万円"
    accumulation = 0
    
    frequency_table = pd.DataFrame() 
    frequency_table["階級"] = df["以上"]+"以上" +class_unit+df["未満"]+class_unit+"未満"
    df = df.replace("-",0)
    for col in df.columns:
        df[col] = df[col].astype(int)
    frequency_table["階級値"] = calc_class_value(df)
    frequency_table["度数"] = list(map(int,df["度数"]))
    frequency_table["相対度数"] = calc_relative_frequency(frequency_table["度数"],mode="frequency")
    frequency_table["累積度数"] = [accumulation := accumulation + i for i in frequency_table["度数"]]
    frequency_table["累積相対度数"] = calc_relative_frequency(frequency_table["累積度数"],mode="accumulation")
    total_data = {"階級":" ","階級値":" ","度数":frequency_table["度数"].sum(),"相対度数":frequency_table["相対度数"].sum(),"累積度数":" ","累積相対度数":" "}
    total_data_row = pd.DataFrame([total_data])
    frequency_table = pd.concat([frequency_table,total_data_row], ignore_index=True)
    print(frequency_table)
    frequency_table.to_csv("frequency_table.csv")

「frequency_table.csv」に度数分布表が出力されます。

度数分布表の各項目はそれぞれ次の意味を持ちます。

• 階級（class）：データの取りうる値を分割した区分
• 度数（frequency）：それぞれの階級に当てはまるデータの数
• 階級値：階級の代表値。階級の中間値をとることが多い
• 相対度数：全体のうちの階級の割合
• 累積度数：度数の累積数
• 累積相対度数：その階級までの相対度数の和

ヒストグラム

ヒストグラムでデータを表すことで、データの傾向やばらつき具合を把握しやすくなります。
度数分布表を使って、度数のヒストグラムを見てみましょう。

import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib

if __name__ == "__main__":
    df = pd.read_csv( "frequency_table.csv")
    df = df[:-1]
    imcome_ranges=df["階級"]

    imcome_num = df["度数"]

    # ヒストグラムを描画
    plt.bar(imcome_ranges, imcome_num)

    # グラフのタイトルとラベル
    plt.title("Income Distribution")
    plt.xlabel("Income Range")
    plt.ylabel("frequency")
    plt.xticks(rotation=90)

    # グラフを表示
    plt.show()

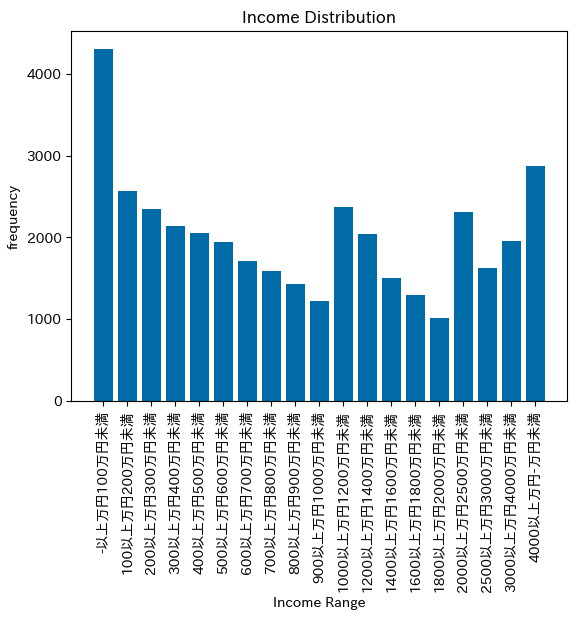
ヒストグラムを見ると、「100万円未満」が最も多いですが、「1000～1200万円」や「4000万円以上」でも山が見られます。
性質の異なるデータが混ざっていると、このようにヒストグラムの山が複数見られることがあります（このようなデータを「多峰性」といいます）。
元の貯蓄データに世帯主の年齢を分けた項目があるので、若年層と高齢層で貯蓄額のヒストグラムを見てみましょう。

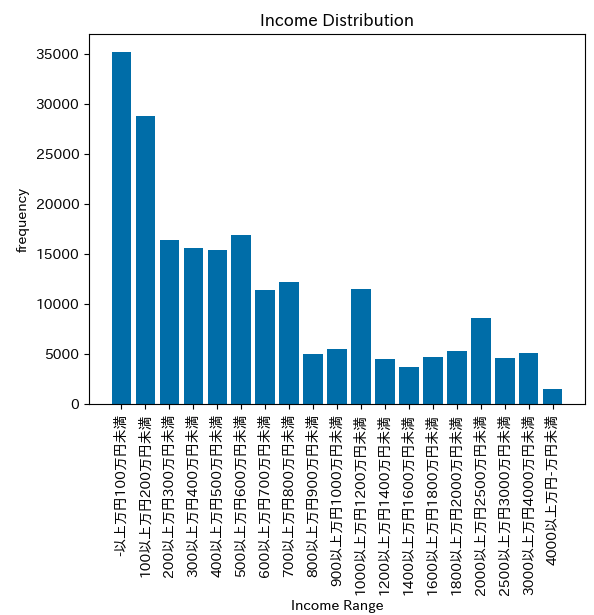
30-34歳の勤労世帯の貯蓄データ

60-64歳の勤労世帯の貯蓄データ

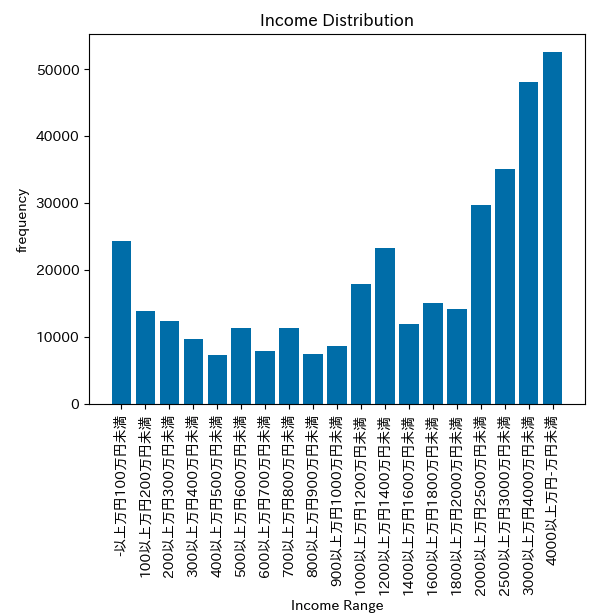
年齢層が絞り込まれたことで、データの傾向が先ほどよりも読み取りやすくなりました。
また、当たり前のことではありますが、年齢層によりボリュームゾーンが右に寄っていく(= 貯蓄額は増えていく)ことがデータから読み取れました。

階級の決め方

今回は政府統計のデータを拝借して題材としているため、階級がすでに決まっています。
しかし、自分たちで集めたデータが n 個あるときの階級を定めたい時、どのようにすれば良いでしょうか。
まず階級数については、目安としてスタージェスの公式が利用できます。

import math


def calc_sturges(n):

    return int(1+math.log2(n))

階級の決め方については、一般には以下のように定める場合が多いです。

• 階級幅はなるべく一定にする
• 度数が極端に少なくなる場合、階級幅を広げる
• 階級の上限・下限値はなるべく区切りの良い値を採用する

階級が細かすぎたり、逆に大まかすぎたりすると、データの正しい分布状況を把握することが難しくなります。
そのため、データの特性を踏まえた上で、試行錯誤して適切な階級幅を決めると良いです。

値の範囲が決まっていない階級の対応

本記事の度数分布表のように、最初や最後の階級で値の範囲が定まっていない場合があります。
このような階級は、諸々の分析で利用しにくいことがあります。
その場合、次の2つの方法で対処が可能です。

1. 階級ごと外れ値として除く

最初と最後の階級の度数が合わせて全体の数%しかない場合、この2つの階級を外れ値として除いてしまう方法です。

度数分布表を例にとると、最初と最後の階級は7,182件で、度数全体が38,318件です。
よって、最初と最後の階級には度数全体のうち約19%が属していることがわかります。
19%は外れ値として無視するには大きすぎる値のため、この度数分布表においては階級を除くことは適切ではありません。

2. 値の範囲を決めてしまう

階級を外れ値として除けない場合、値を仮定して利用する方法があります。
データにより適切な値を決める必要がありますが、今回は度数分布表を例に求めてみましょう。

貯蓄の最低額は0より下はないはずなので、最初の階級の下限値は0と仮定します。
よって最初の階級は、0万円以上~100万円未満とみなせます。なので、階級値はその中間である50と仮定できます。
貯金の最高額は青天井ですが、直前の階級と同じ階級幅で上限値を仮定することが一般的です。
よって最後の階級は、直前の階級が3000万円以上~4000万円未満で階級幅が1000万円のため、上限を5000万円と仮定します。
そして4000万円以上〜5000万円未満の階級の階級値は、4500万円と仮定できます。
これで、度数分布表で使用した度数分布表の、最初と最後の階級の値およびその階級値を仮定できました。
ヒストグラムの章では、この方法で階級を決めています。

留意すべきこととして、この方法で決めた階級はあくまで仮定であるということです。
特に上限値が小さく見積もられてしまう傾向にあるため、この方法で求めた階級値をもとに平均値を出す場合、真の値より小さい値が出てしまうことがあります。

複数のデータセットの傾向を比較する

ヒストグラムは、単一のデータセットの傾向を把握するのに非常に便利なものです。
しかし、複数のデータセットの傾向を比較したいときには、ヒストグラムを横に並べて見比べてもぱっと見でわかりにくいです。
この章では、複数のデータセットの傾向を比較する場合を考えてみましょう。

題材

この章では統計学や機械学習などの分野の解説でよく使われる「Irisデータセット」を題材とします。
Irisデータセットは、あやめの仲間である「setosa」「versicolor」「virginica」という3種類の花についてのデータセットです。
3種類の花の特徴のうち、「sepal length(cm)」（がく片の長さ）を比較してみます。

箱ひげ図

箱ひげ図では、データの中央値や四分位範囲、外れ値などをひとつの図に表すことができます。
分布の範囲を簡潔に示すことで、データの中心や傾向を視覚的に確認できます。
以下のように比較したいデータセットの箱ひげ図を並べることで、データセットごとの傾向を比較することも容易です。

from sklearn.datasets import load_iris
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
iris = load_iris()

df = pd.DataFrame(iris.data, columns=iris.feature_names)
df["label"] = iris.target_names[iris.target]

# 箱ひげ図を描画
plt.figure(figsize=(12, 8))
sns.boxplot(x='label', y='sepal length (cm)', data=df)
plt.title('Sepal Length Comparison across Iris Species')
plt.show()

3種類の花のがく片長さのデータが可視化できたことで、花ごとの特徴が一目で比較できるようになりました。
「virginica」には外れ値があることや、「virginica」>「versicolor」>「setosa」の順にがく片が長い傾向にあることが読み取れます。

バイオリン図

バイオリン図は中央値や四分位範囲に加え、カーネル密度推定に基づいたデータの形状を表すことができます。
バイオリンの幅はデータの頻度を表しています。
そのため、幅が大きい部分 = 数が多いと言えます。
また、バイオリンの長さはデータの広がりを表しています。
よって、長さからはデータのばらつきの程度を読み取ることができます。

Python では、箱ひげ図のコードの描画部分を変えることで簡単に表示できます。

# バイオリン図を描画
plt.figure(figsize=(12, 8))
sns.violinplot(x='label', y='sepal length (cm)', data=df)
plt.title('Sepal Length Comparison across Iris Species')
plt.show()

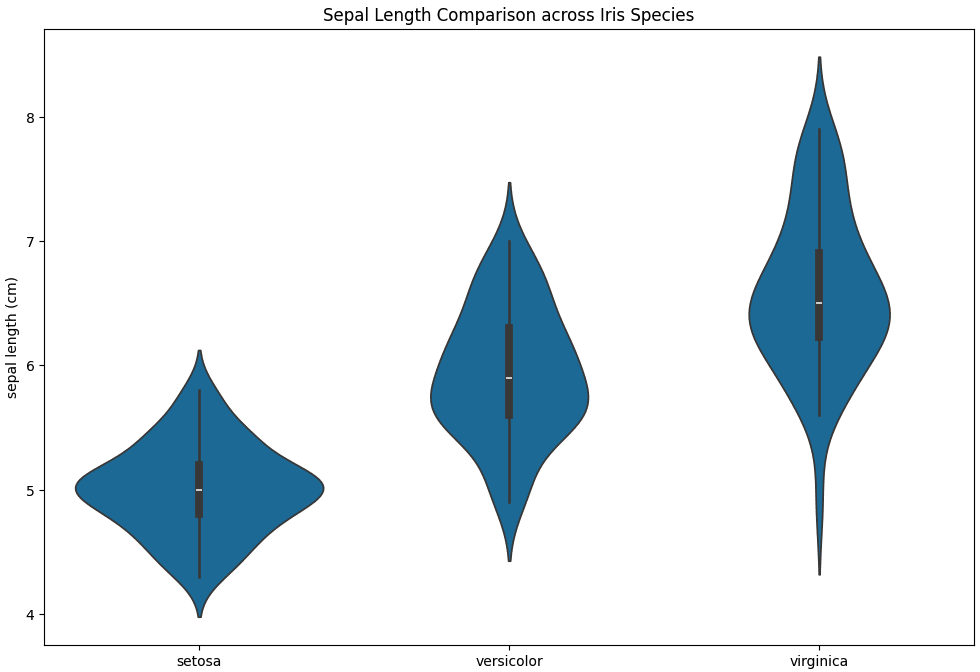
箱ひげ図よりも詳細にデータの分布が可視化できました。
「virginica」>「versicolor」>「setosa」の順にがく片長さにばらつきが大きいことが読み取れます。
また、バイオリンの形状から、3種類ともピークが一つでおおむね対照的に分布（正規分布）していることもわかります。

使い分け

箱ひげ図とバイオリン図は、どちらもデータの分布を可視化する手法です。
箱ひげ図は四分位範囲のようなデータの中心傾向を簡潔に表すことができます。
そのため、データの中心がどこにあるのか、外れ値がどの程度存在するかを簡潔に比較・確認したい場合に利用できます。
バイオリン図は、データの全体的な形状を詳細に表すことができます。
そのため、データ全体の形状を含めて比較・確認したい場合に利用できます。

外れ値について

一般的に、四分位範囲の1.5倍を超える範囲にある値を外れ値とすることが多いです。
外れ値はデータの中心から大きく外れているため、統計分析や機械学習等で利用する際に影響を与えることがあります。
対処としては、外れ値を除外・補完したり、データ全体を対数変換する等の方法があります。

除去や補完はイメージがしやすいかと思います。
対数変換は、大きな値の外れ値が小さな値に変換することができます。
そののため、右に裾の長い分布を正規分布に近づけられる場合があります。

import numpy as np
import matplotlib.pyplot as plt

lambda_param = 0.2
# 指数分布に基づくデータ生成
data = np.random.exponential(scale=1/lambda_param, size=1000)
# 対数変換
log_transformed_data = np.log1p(data)

plt.figure(figsize=(12, 6))

# 元のデータのヒストグラム
plt.subplot(1, 2, 1)
plt.hist(data, bins=30, density=True, color='blue', alpha=0.7)
plt.title('Original Data (Exponential Distribution)')

# 対数変換後のデータのヒストグラム
plt.subplot(1, 2, 2)
plt.hist(log_transformed_data, bins=30, density=True, color='green', alpha=0.7)
plt.title('Log-transformed Data')

plt.show()

データの性質、分析の目的により外れ値の対応に適した方法は異なります。
そのため、そもそも外れ値が何を意味しているのか（入力誤りなのか、特異なデータなのか）の理解やデータの収集方法、ドメインの知識を考慮することが必要です。

おわりに

Workbench のインスタンスを停止または削除、および BigQuery のテーブルを削除するのをお忘れなきようご注意ください。
最後まで読んでいただきありがとうございました。
データ分析をする上で参考になれば幸いです。