Zenn
📈

【Shubert-Piyavskii法】極値が複数あっても最大・最小を求める

2023/09/17に公開
競技プログラミング
AtCoder
数理最適化
アルゴリズムとデータ構造
tech

はじめに

とある関数の最大値・最小値を求めたくなるケースがある．
効率的な手法として主に考えられる手法は三分探索・黄金分割探索等である．
ところが，これらの手法は極値が1つの場合しか使用できないという弱点がある．
そういった場合にも最大・最小を求めたい場合も勿論あるだろう．
パフォーマンスは三分探索と比べるとかなり劣るが，Shubert-Piyavskii法と呼ばれるアルゴリズムを用いると解決できる場合がある．
これを取り上げている日本語の記事があまりないようであるため，ここにまとめることにした．

使える条件

目的関数がリプシッツ連続であること．

リプシッツ連続（Lipschitz continuity）

関数f:\left[a,b\right] \rightarrow \mathbb{R}がリプシッツ連続であるとは，あるl>0が存在して以下の条件を満たすことをいう．

\left|f(x)-f(y)\right|\leq l\left|x-y\right|~x,y\in \left[a,b\right]

lの最小値のことをリプシッツ定数と呼ぶ．
直感的には，lは瞬間変化率の大きさの最大値であるといえる．

因みに，fが微分可能である場合，fがリプシッツ連続であることとf'が有界であることは同値である．

証明

まず，fがリプシッツ連続ならばf'が有界であることを示す．
定義より，x<yに対して

\left|\frac{f(x)-f(y)}{x-y}\right|\le l

y\to xとすると，|f'(x)|\le lより成立．

次に逆を示す．
平均値の定理より，x<yに対して以下を満たすc~(x<c<y)が存在する．

\left|\frac{f(x)-f(y)}{x-y}\right|=|f'(c)|\le l

以上より示された．

アルゴリズムの流れ

Step1. 中点x_0=(a+b)/2を求める．
Step2. 勾配\pm lの半直線を(x_0,f(x_0)), (a,f(a)), (b,f(b))から引き，のこぎり歯を構築する．
Step3. 半直線同士の交点を左右それぞれ求め，点リスト\mathcal{T}に2つの交点と(a,f(a)),(x_0,f(x_0)),(b,f(b))の5点をx座標順に挿入する．
Step4. \mathcal{T}の中でy座標が最小の点xに対し，点(x, f(x)から勾配\pm lの半直線をStep2と同様に引く．
Step5. 引いた半直線とのこぎり歯との交点を左右それぞれ求める．（交点をそれぞれL,Rとする）
Step6. \mathcal{T}のx=x_minなる点を点(x_{min},f(x_{min}))に置き換え，その前にL，後にRを挿入する．
Step7. y座標の最小値（y'_{min}）と，yの最小値を持つx'_{min}に対し，f(x'_{min})-y'_{min}\ge\epsilonならばStep4に戻る．
Step8. \{(x,y)\in\mathcal{T}\;|\; y=f(x)\}の中でyの最小値を出力する．

動作の様子

のこぎり歯で関数の下界を絞っているのがわかるだろう．

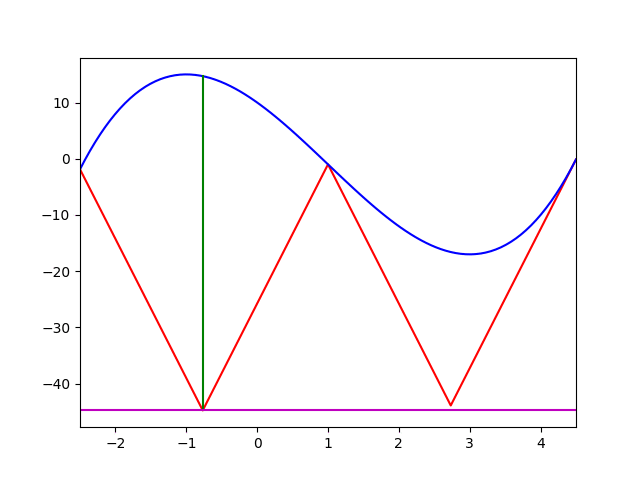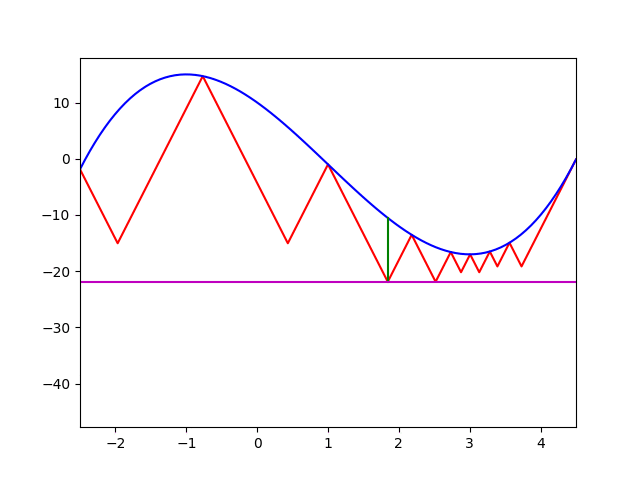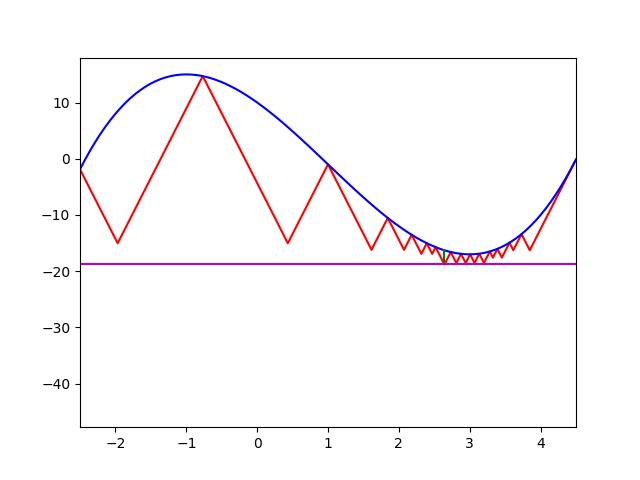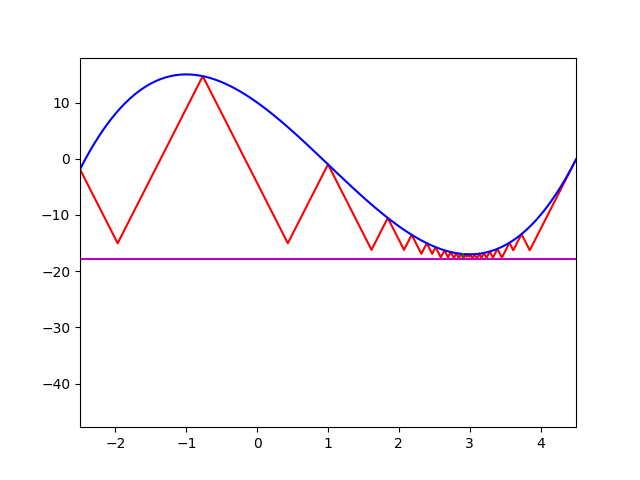
実装例

C++
double shubert_piyavskii(double left, double right, double lipschitz_constant, function<double(double)> f)
{
    auto get_intersection = [&](pair<double, double> a, pair<double, double> b)
    {
        double t = ((a.second - b.second) - lipschitz_constant * (a.first - b.first)) / (2 * lipschitz_constant);
        return make_pair(a.first + t, a.second - t * lipschitz_constant);
    };
    auto cmp = [&](pair<double, double> a, pair<double, double> b)
    {
        return a.second < b.second;
    };

    double middle = (left + right) / 2;
    pair<double, double> left_point = {left, f(left)}, middle_point = {middle, f(middle)}, right_point = {right, f(right)};

    vector<pair<double, double>> points = {left_point, get_intersection(left_point, middle_point), middle_point, get_intersection(middle_point, right_point), right_point};

    double delta = 1e32, eps = 1e-6;
    while (delta > eps)
    {
        ll min_idx = min_element(all(points), cmp) - points.begin();
        pair<double, double> min_point = points[min_idx];
        pair<double, double> point_on_f = make_pair(min_point.first, f(min_point.first));
        delta = fabs(point_on_f.second - min_point.second);

        pair<double, double> point_prev = get_intersection(points[min_idx - 1], point_on_f);
        pair<double, double> point_next = get_intersection(point_on_f, points[min_idx + 1]);

        points.erase(points.begin() + min_idx);
        points.insert(points.begin() + min_idx, point_next);
        points.insert(points.begin() + min_idx, point_on_f);
        points.insert(points.begin() + min_idx, point_prev);
    }

    vector<pair<double, double>> points_on_f;
    for (ll i = 0; i < points.size(); i += 2)
    {
        points_on_f.push_back({points[i].first, points[i].second});
    }

    return min_element(all(points_on_f), cmp)->second;
}
Rust
fn shubert_piyavskii(left: f64, right: f64, lipschitz_constant: f64, f: &dyn Fn(f64) -> f64) -> f64 {
    let get_intersection = |a: (f64, f64), b: (f64, f64)| -> (f64, f64) {
        let t = ((a.1 - b.1) - lipschitz_constant * (a.0 - b.0)) / (2.0 * lipschitz_constant);
        (a.0 + t, a.1 - t * lipschitz_constant)
    };

    let middle = (left + right) / 2.0;
    let left_point = (left, f(left));
    let middle_point = (middle, f(middle));
    let right_point = (right, f(right));

    let mut points = vec![
        left_point,
        get_intersection(left_point, middle_point),
        middle_point,
        get_intersection(middle_point, right_point),
        right_point,
    ];

    let mut delta = 1e32;
    let eps = 1e-6;

    while delta > eps {
        let min_idx = points
            .iter()
            .enumerate()
            .min_by(|(_, a), (_, b)| a.1.partial_cmp(&b.1).unwrap())
            .unwrap()
            .0;

        let min_point = points[min_idx];
        let point_on_f = (min_point.0, f(min_point.0));
        delta = (point_on_f.1 - min_point.1).abs();

        let point_prev = get_intersection(points[min_idx - 1], point_on_f);
        let point_next = get_intersection(point_on_f, points[min_idx + 1]);

        points.remove(min_idx);
        points.insert(min_idx, point_next);
        points.insert(min_idx, point_on_f);
        points.insert(min_idx, point_prev);
    }

    let points_on_f: Vec<(f64, f64)> = points.iter().step_by(2).copied().collect();

    points_on_f
        .iter()
        .min_by(|a, b| a.1.partial_cmp(&b.1).unwrap())
        .unwrap()
        .1
}

動作例

f(x)=x^3-3x^2-9x+10~(-\frac{5}{2}\leq x \leq \frac{9}{2})を例にして実装した．
グラフは以下の通りである．

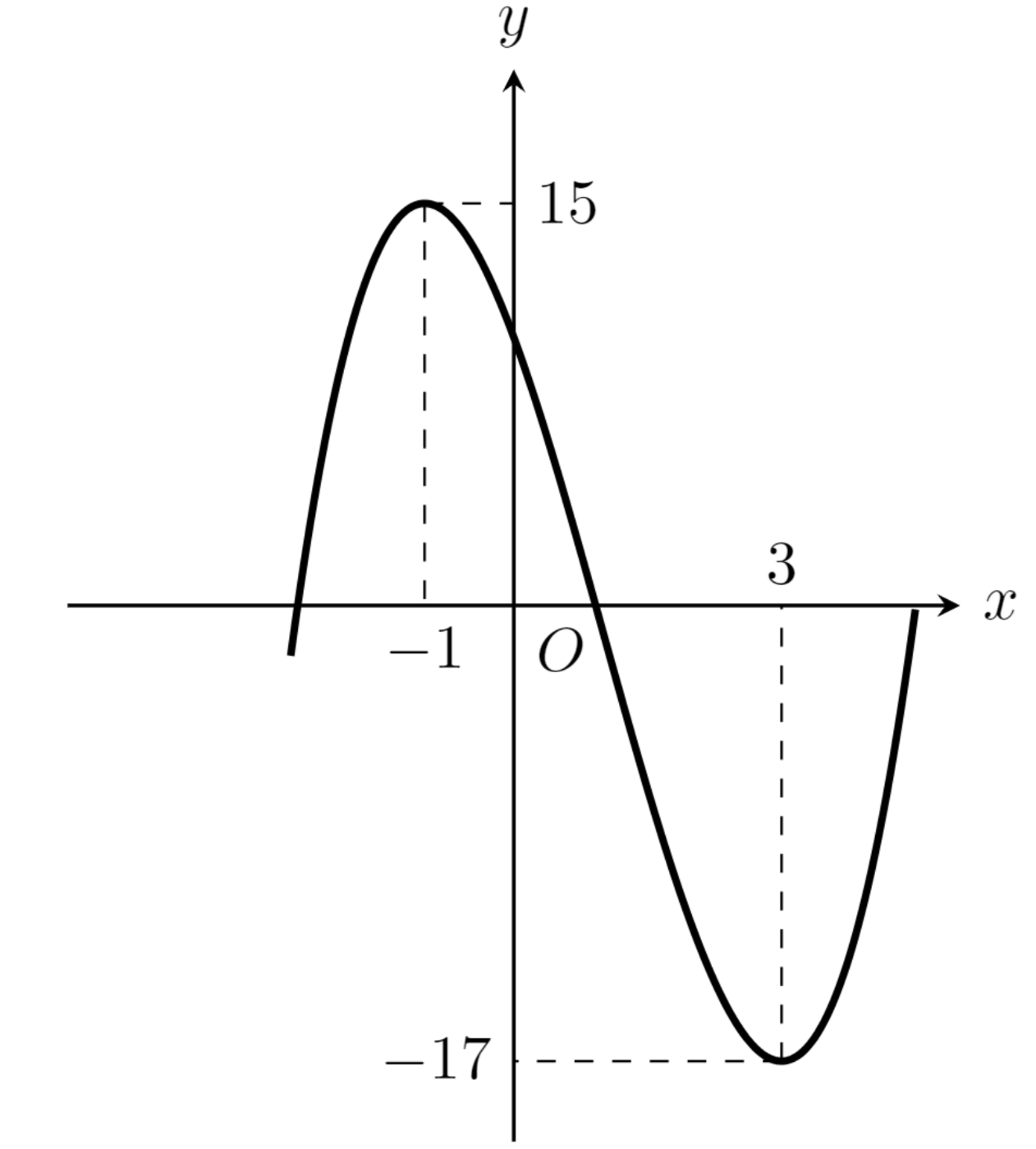
極値が2つあり，三分探索で求めるのは難しそうである．こういった場合にShubert-Piyavskii法を用いると良い．

main関数の実装（C++）
int main()
{

    auto f = [&](double x)
    {
        return powf(x, 3) - 3 * powf(x, 2) - 9 * x + 10;
    };
    auto f_prime = [&](double x)
    {
        return 3 * powf(x, 2) - 6 * x - 9;
    };

    double left = -2.5, right = 4.5;
    double lipschitz_constant = max(fabs(f_prime(left)), fabs(f_prime(right)));

    auto res = shubert_piyavskii(left, right, lipschitz_constant, f);

    cout << res << endl;

    return 0;
}

実際に実行してみると，17と出力されるはずである．
（環境によってはもしかすると17.0000000001や16.999999999998などのように誤差が生じているかもしれない）

計算時間について

Shubert-Piyavskii法では，リストに点を追加し続けている．
三分探索のように区間を区切る処理はないため，パフォーマンス面ではかなり劣っている．
また，ループ回数は集合の区間の長さ，\epsilon，fによって変化する．

計測結果

動作例で\epsilonを変化させて計算時間を計測した．言語はRustを使用した．

\epsilon 実行時間(s)
1e-1 0.000017404556274414063
1e-2 0.00006794929504394531
1e-3 0.0004591941833496094
1e-4 0.003313779830932617
1e-5 0.06352639198303223
1e-6 0.5958070755004883
1e-7 5.486490488052368
1e-8 102.90221571922302

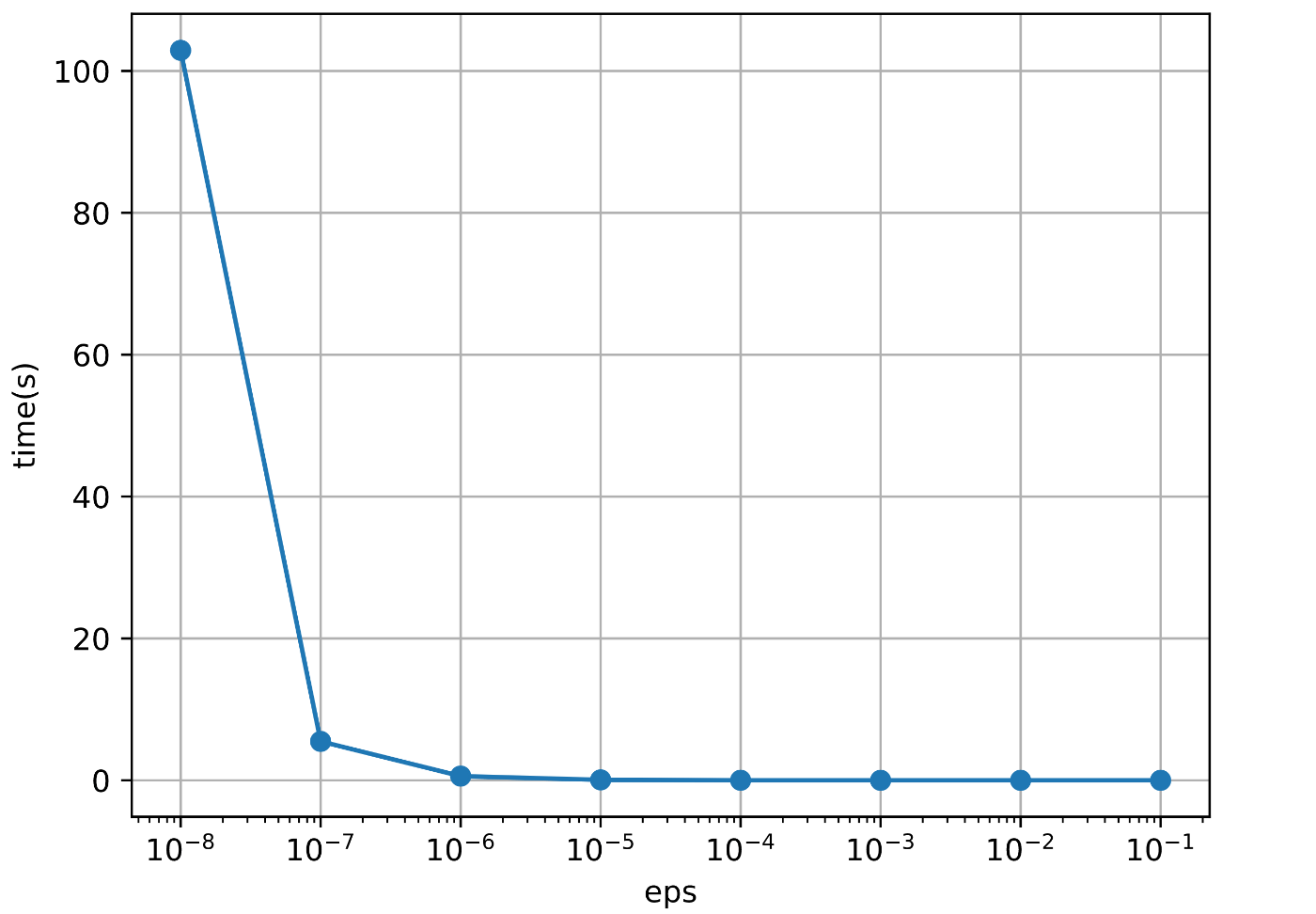
精度を重視しすぎると大変なことになるので，使いどころに注意である．

さいごに

極値が複数ある関数でも最大値最小値を求められるアルゴリズムを紹介した．
割と強力な一方で，実行時間が大分長くなってしまうので競技プログラミングで応用する機会はあまりなさそうではある．
とはいえ，制限時間が緩めなヒューリスティックコンテストなどにおいて，精度を重視しなくともおおよその最大最小を見積もりたい場面では大変有用であると考えられるので，一人でも多くの方に参考になれば幸いである．

参考文献

Discussion