Zenn
📈

Scipy の Lomb-Scargle ピリオドグラムを使う

2022/09/06に公開
Python
データ分析
時系列データ
tech

概要

時系列データの周期性解析で Lomb-Scargle 法を使う場面が最近あった。
Lomb-Scargle 法はいくつかのライブラリで提供されているようだが、今回は Scipy で提供されるモジュールを使用した。備忘録として使用法をメモしておく。

Lomb-Scargle ピリオドグラムとは

Lomb-Scargle ピリオドグラム（Lomb (1976)[1], Scargle (1982)[2]）とは、不規則にサンプリングされた時系列データから、周期性を見つけ出す統計的手法である。
周期性の解析に用いられる手法として、高速フーリエ変換（Fast Fourier Transform, FFT）などの手法が挙げられるが、この手法はデータのサンプリングの間隔が一定である場合にしか使うことができない。
天文学や地球物理学などの分野では、サンプリングの時間間隔が一定でないデータを取り扱う場面が多く、このような場面での周期性解析に Lomb-Scargle ピリオドグラムが用いられる。

Scipy モジュールを使った実装

Scipy から Lomb-Scargle ピリオドグラムを使用するためのモジュール scipy.signal.lombscargle が提供されている。
このモジュールを用いて、適当な時系列データを対象に、Lomb-Scargle ピリオドグラムを計算し、描画してみる。
ここでは Statsmodels が提供する 1700 年 ~ 2008 年の年間の太陽黒点発生数のデータを使用する。

# データのロードと時系列プロット
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm
import scipy.signal as signal

df_sunspot = sm.datasets.sunspots.load_pandas().data
x = df_sunspot["YEAR"]
y = df_sunspot["SUNACTIVITY"]

fig = plt.figure(figsize=(20, 6))
ax = fig.add_subplot(1,1,1)
ax.set_xlabel("Year")
ax.set_ylabel("Sunspots")
ax.plot(x, y)

fig.show()

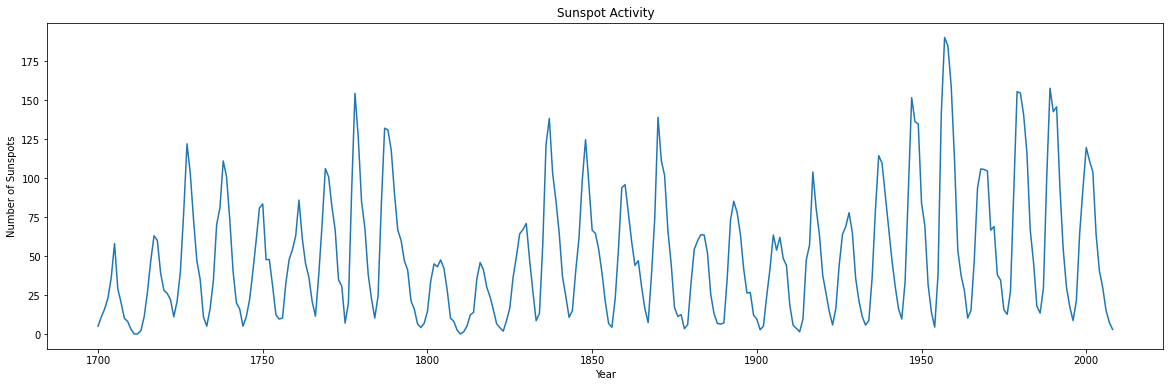
時系列プロットから、このデータは周期性を持っていることが分かる。
なお太陽の黒点数はおよそ 11 年の周期で増減を繰り返すことが観測から知られている[3]。
この時系列データに対して、Lomb-Scargle ピリオドグラムを計算・描画する。

# Lomb-Scargle ピリオドグラムの計算と出力
x = df_sunspot["YEAR"]
y = df_sunspot["SUNACTIVITY"]
periods = np.linspace(0.1, 30, 1000)
ang_freq = 2 * np.pi / periods

pgram = signal.lombscargle(
    x, 
    y, 
    ang_freq,
    precenter = True,
    normalize = True
)

fig = plt.figure(figsize=(20, 6))
ax = fig.add_subplot(1,1,1)
ax.set_title("Lomb-Scargle Periodgram")
ax.set_xlabel("Period (year)")
ax.set_ylabel("Power")
ax.set_xticks(np.arange(0,31))
ax.plot(periods, pgram)

fig.show()

11 年の付近にピークを持つピリオドグラムが出力され、観測事実と整合することが確認できる。

使用時の注意点

パラメータ freq には角周波数を与える

Scipy の公式ドキュメントを確認すると、scipy.signal.lombscargle の パラメータ freq には角周波数（≠周波数）を与える必要がある。

freqs : array_like
    Angular frequencies for output periodogram.

パラメータ precenter には True を指定する

scipy.signal.lombscargle には optional のパラメータで precenter というものが設定できる。

precenter : bool, optional
    Pre-center measurement values by subtracting the mean.

Trueにしたときは引数の y （今回の例だと黒点の発生数）から、y の平均値を差し引く処理を、ピリオドグラムを計算する際の前処理として行ってくれる。デフォルトは False である。
Lomb-Scargle ピリオドグラムの計算は precenter 処理が行われた値が前提となっている[4]。

個人的にはこの precenter のパラメータは、デフォルトで True にしたほうが良いのでは？と思うが、precenter が実装された経緯が書かれている Github の Issue を確認したところ、すでに precenter がなされているデータを使用する場合は、この前処理が冗長になってしまうため、それを防ぐためにデフォルトが False の仕様となっているようだった。

脚注

  1. Lomb, N. R., “Least-Squares Frequency Analysis of Unequally Spaced Data”, <i>Astrophysics and Space Science</i>, vol. 39, no. 2, pp. 447–462, 1976. doi:10.1007/BF00648343. ↩︎

  2. Scargle, J. D., “Studies in astronomical time series analysis. II. Statistical aspects of spectral analysis of unevenly spaced data.”, <i>The Astrophysical Journal</i>, vol. 263, pp. 835–853, 1982. doi:10.1086/160554. ↩︎

  3. Hathaway, D.H. The Solar Cycle. Living Rev. Sol. Phys. 12, 4 (2015). https://doi.org/10.1007/lrsp-2015-4 ↩︎

  4. Fast Lomb-Scargle Periodograms in Python ↩︎

Discussion