自作プログラミング言語を初級者が1週間で作る方法 (7) リストと高階関数

自作プログラミング言語をなるべく簡単に作る方法を紹介します。また、実際に自作プログラミング言語を作ってみます。

前回の記事で Yuz 言語が一旦完成しました。今回は Yuz 言語の書き味を確かめてみるために、実際に Yuz 言語を使ってリストと高階関数のプログラムを書いてみます。

リスト

ここでは片方向連結リストを作ってみます。例として

• 4, 6, 3, 7, 1, 5, 2

という 7 個の数値を持つリストを作ります。このリストの名前を nums とします。リストをよく使う言語はリスト用の構文を用意していて

let nums = [4, 6, 3, 7, 1, 5, 2];

のようにリストを作ることができます。Yuz 言語にはリスト用の機能がないので一から作ってみることにします。リストの構造は次のようになります。

リストの各項は head と tail で構成されます。head にはその項の値を入れて、tail には次の項を入れます。最終項は tail に nil を入れて行き止まりにします。リストの項を作る関数を cons とすると

let cons = \x -> \xs -> {head: x, tail: xs};

となります。これを使うとリストの最終項 node_7 とその一つ前の項 node_6 は

let node_7 = cons[2][nil];
let node_6 = cons[5][node_7];

と作ることができます。cons[a][b] は a `cons` b と書くこともできます。また、`cons` は右結合なので a `cons` b `cons` c は a `cons` (b `cons` c) の順で計算されます。よって冒頭で示したリストは

let nums = 4 `cons` 6 `cons` 3 `cons` 7
           `cons` 1 `cons` 5 `cons` 2 `cons` nil;

と一気に作ることができます。このリストの先頭にさらに 10 を付け足したくなったときは

10 `cons` nums

とすればいいです。実際に試してみると下記のようになります。

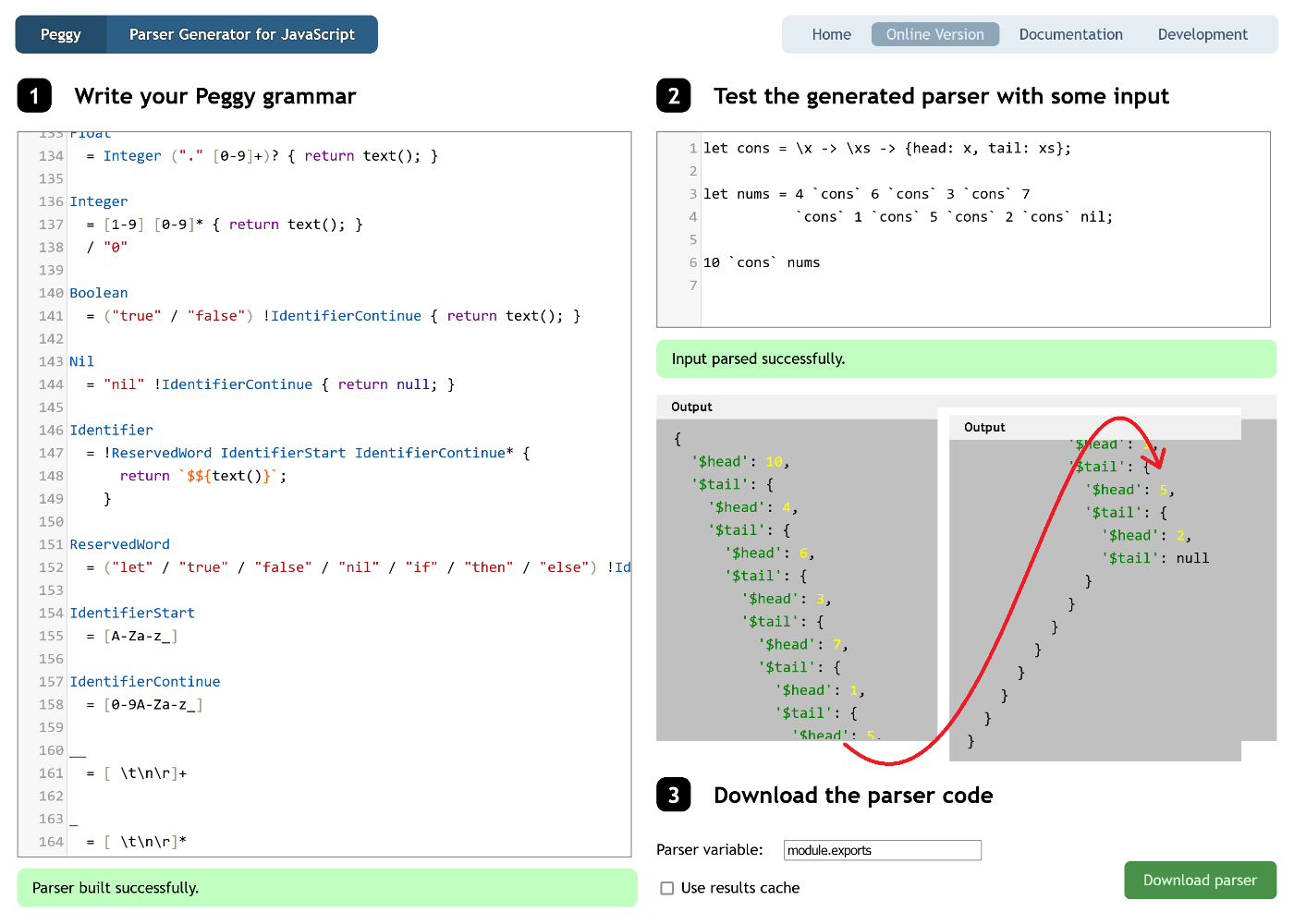
確かにリストの構造が出来上がっていることがわかります。

自己再帰関数

リストを操作するためには自己再帰関数が必要になります。まずは確認のために自己再帰関数を使った簡単なプログラムを書いてみます。

階乗

$n$ の階乗を求めるプログラムを作ります。

• $n! = n \times (n - 1) \times (n - 2) \times \dots \times 3 \times 2 \times 1$

$n$ の階乗を求める関数を fact[n] とします。fact[n] は漸化式を使って

• fact[0] は 1
• fact[n] は n * fact[n - 1]

と表すことができます。したがって、関数 fact を Yuz 言語で書くと

let fact = \n -> if n == 0 then 1 else n * fact[n - 1];

となります。たとえば fact[8] は 8 * 7 * 6 * ... * 1 で 40320 となります。

高階関数

リストを操作するための高階関数を作ってみます^[1]。

畳み込み

まずは最も基本的な高階関数である foldr を作ってみます。foldr は

• 4, 6, 3, 7, 1, 5, 2

というリスト nums に対して foldr[f][ini][nums] としたときに

4 `f` 6 `f` 3 `f` 7 `f` 1 `f` 5 `f` 2 `f` ini

を計算してくれる関数です。リストに格納された大量のデータに対して関数 `f` をはさんだ一括計算をしてくれます。たとえばリストの全要素を合計する計算

4 + 6 + 3 + 7 + 1 + 5 + 2

は foldr で `f` を + に、ini を 0 にすれば計算できます。

foldr を Yuz 言語で作ると

let foldr = \f -> \ini -> \xs -> (
    if xs == nil then (
        ini
    ) else (
        xs.head `f` foldr[f][ini][xs.tail]
    )
);

となります。リスト xs の要素を合計する関数を sum[xs] とすると

let add = \a -> \b -> a + b;
let sum = \xs -> foldr[add][0][xs];

となります。2 行目は関数の部分適用を用いて

let sum = foldr[add][0];

と書くこともできます。

実際に nums の要素の合計を求めると 28 となります。

マップ

有名な高階関数の一つである map を作ってみます。map は

• 4, 6, 3, 7, 1, 5, 2

というリスト nums に対して map[f][nums] としたときに

• f[4], f[6], f[3], f[7], f[1], f[5], f[2]

というリストを返してくれる関数です。リストに格納された大量のデータに対して一括で関数 f を適用してくれます。map は foldr を使って

let map = \f -> foldr[\x -> \xs -> f[x] `cons` xs][nil];

と作ることができます。

フィルター

リストから特定の条件を満たす要素だけを抜き出す関数 filter を作ってみます。

let filter = \p -> foldr[\x -> \xs -> if p[x] then x `cons` xs else xs][nil];

使用例として、リスト nums があったときに、このリストから奇数だけを抜き出した新たなリストを作るプログラムは

let is_odd = \x -> x % 2 == 1;

let nums = 4 `cons` 6 `cons` 3 `cons` 7
           `cons` 1 `cons` 5 `cons` 2 `cons` nil;

filter[is_odd][nums]

となります。このプログラムの出力は 3, 7, 1, 5 のリストです。

リスト同士の連結

二つのリスト xs と ys を連結して一つのリストにする関数 append は

let append = \xs -> \ys -> foldr[cons][ys][xs];

となります。たとえば xs が 1, 2, 3, 4 で ys が 8, 9, 10 のときに append[xs][ys] または xs `append` ys とすると 1, 2, 3, 4, 8, 9, 10 を得ます。

クイックソート

filter と append を使ってクイックソートを作ってみます。クイックソートはリストの要素を小さい順に並べ替える関数です。

let quicksort = \xs -> (
    if xs == nil then (
        nil
    ) else (
        let lt = filter[\y -> y < xs.head][xs.tail];
        let gteq = filter[\y -> y >= xs.head][xs.tail];
        quicksort[lt] `append` xs.head `cons` quicksort[gteq]
    )
);

実際に試してみると、次のように小さい順にソートされたリストを得ることができます。

let nums = 4 `cons` 6 `cons` 3 `cons` 7
           `cons` 1 `cons` 5 `cons` 2 `cons` nil;

quicksort[nums]

パイプライン

処理を一つずつ順番に行っていくときにパイプラインという高階関数を使います。

let pipe = \x -> \f -> f[x];

func[a][b] は a 'func' b と書くことができ、こう書いたときは左結合となります。リスト nums があったときに

1. 奇数の要素を取り出し、
2. 要素を 2 乗し、
3. 総和を求める

という順の計算は

let nums = 4 `cons` 6 `cons` 3 `cons` 7
           `cons` 1 `cons` 5 `cons` 2 `cons` nil;

nums 'pipe' filter[is_odd] 'pipe' map[\x -> x * x] 'pipe' sum

となります。この計算は 3 * 3 + 7 * 7 + 1 * 1 + 5 * 5 で 84 となります。

まとめ

Peggy で自作した Yuz 言語を使ってリストと高階関数のプログラムを書いてみました。Peggy を使うことでこのように手軽に自作言語を作ってその書き味を確かめてみることができます。

脚注

1. この記事では foldr、map、filter などを Yuz 言語で作ってみますが、コードの内容をすぐに理解することは容易ではありません。これは Yuz 言語というよりも高階関数が難しいためです。