Zenn
✅

中間層設計

に公開
学習記録
ニューラルネットワーク
idea

はじめに

概要

  • シラバス：E資格2024#2
  • 中間層で使用する活性化関数を勉強します

モデル訓練のステップ

  1. アーキテクチャの設計
  2. 入力層設計
  3. 中間層設計
  4. 出力層設計
  5. 誤差計算
  6. モデルに誤差を反映する
  7. 重みの更新の設定をする
  8. 最適なモデルを手に入れる

キーワード

ステップ関数, シグモイド関数, 勾配, tanh関数,
ReLU関数, PReLU関数, Leaky ReLU関数, GELU

学習内容

ステップ関数

  • 閾値を境にして出力が切り替わる関数です

  • 問題点

    • 出力が0か1しかないため、表現力が低いです
    • 学習に必要な「勾配」が存在しません
    • 出力が不連続なので、入力のわずかな違いに反応できません
f(x) = \begin{cases} 1 & (x \geq 0) \\ 0 & (x < 0) \end{cases}

シグモイド関数(sigmoid function)

  • 入力された値が大きければ大きいほど1に近づき、入力した値が小さければ小さいほど0に近づく関数です
  • 特徴
    • x=0 のとき、出力は 0.5
    • x→+∞ のとき、出力は 1 に近づく
    • x→−∞ のとき、出力は 0 に近づく
  • 問題点：
    • 逆伝播の際、入力層に近いところで学習が進みにくい(微分値の最大値が0.25のため、学習の収束が遅い)　→　勾配消失（vanishing gradient）
    • 入力が大きく(小さく)なるほど勾配が消える
f(x)=\frac{1}{1+e^{-x}}=\frac{e^{x}}{e^{x}(1+e^{-x})}=\frac{e^{x}}{1+e^{x}}

微分後

\frac{df(x)}{dx}=f(x)(1-f(x))


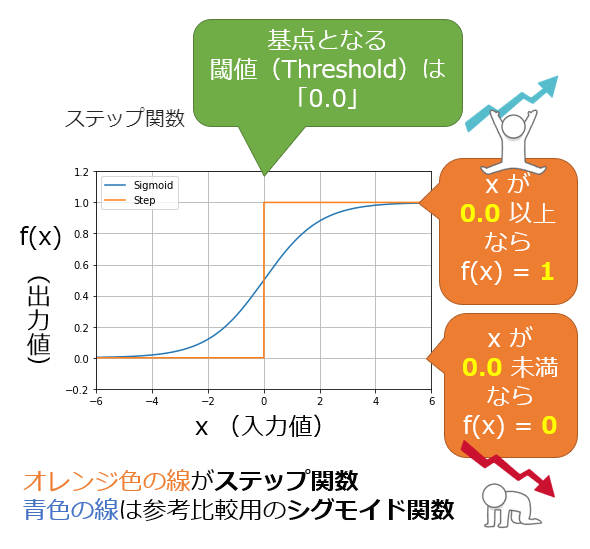
ステップ関数とシグモイド関数の比較
出典：
一色政彦, ［活性化関数］ステップ関数（Step function）とは？(2020), @IT, https://atmarkit.itmedia.co.jp/ait/articles/2002/26/news010.html

tanh関数 (Hyperbolic tangent function, 双曲線正接関数)

  • -∞から＋∞までのあらゆる数値を-1から+1の間に収まるように出力します
  • メリット
    • 微分値の最大値が1なので、入力層近くにおける学習がシグモイド関数より進みやすい
    • 出力が−１から１で出力が0にセンタリングされるため、学習の収束がシグモイド関数よりも容易
  • 問題点
    • シグモイド関数同様、入力が大きく(小さく)なると勾配が消える
f(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}


tanh関数(左)とその微分(右)
出典：
Masaki Hayashi, tanh 関数 活性化関数, @CVMLエキスパートガイド, https://cvml-expertguide.net/terms/dl/layers/activation-function/tanh/


シグモイド関数(左)とtanh関数の比較
出典：
Masaki Hayashi, tanh 関数 活性化関数, @CVMLエキスパートガイド, https://cvml-expertguide.net/terms/dl/layers/activation-function/tanh/

ReLU関数（Rectified Linear Unit）

  • 入力された値が0以下のとき0を出力、0より大きいとき入力をそのまま出力します
  • メリット
    • 微分値が定数なので、計算量を圧倒的に減らせ、バックプロパゲーションの計算効率がいい
    • 勾配消失問題への対処が有効
  • 問題点
    • 入力が負の時微分値が0なので、重みの更新がされない
𝑓(𝑥)=max(0,𝑥)

PReLU(Parametric ReLU)関数

  • 入力された値が0以下のとき、任意の傾きをかけた値を出力、0より大きいとき入力をそのまま出力します
  • ReLU関数の問題を改善して、αはデータに基づいて調整されるため、負の値の傾きを最適化できます(学習できます)
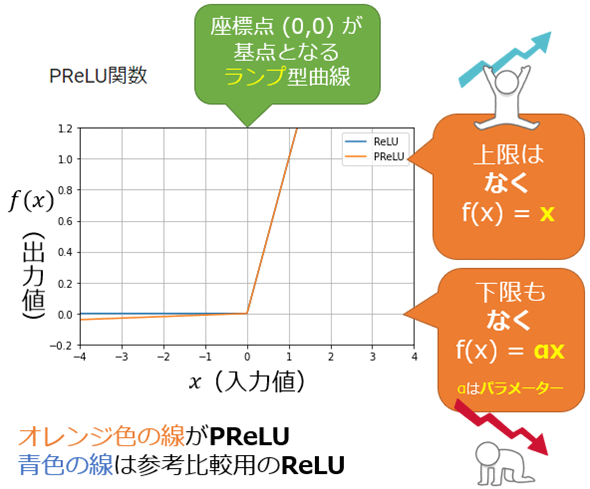
f(x) = \begin{cases} x & \text{if } x \geq 0 \\ \alpha x & \text{if } x < 0 \end{cases}


出典：
一色政彦, ［活性化関数］PReLU／Parametric ReLU（Parametric Rectified Linear Unit）とは？(2020), @IT, https://atmarkit.itmedia.co.jp/ait/articles/2005/20/news010.html

Leaky ReLU関数

  • 入力された値が0以下のとき、ある固定値の傾きをかけた値を出力、0より大きいとき入力をそのまま出力します
    • 固定値は0.01や0.02です
  • ReLU関数の変種のひとつです
  • PReLUと違い、固定された値で学習はされません
f(x) = \begin{cases} x & \text{if } x \geq 0 \\ \alpha x & \text{if } x < 0 (\alpha は固定値) \end{cases}

比較表

関数 数式 負の部分の勾配
ReLU \max(0, x) 0
Leaky ReLU \max(\alpha x, x)（固定α） 固定値（例：0.01）
PReLU \max(\alpha x, x)（学習α） 学習可能

GELU (Gaussian Error Linear Units)

  • ReLUのように単純な「0かx」ではなく、入力の値に応じて滑らかに出力を変化させる点が特徴です
f(x) = x\cdot \Phi(x)=\frac{x}{2} \left[ 1 + \text{erf} \left( \frac{x}{\sqrt{2}} \right) \right]

\Phi(x)は標準正規分布の累積分布関数（CDF）です

\Phi(x)=\frac{1}{2} \left[ 1 + \text{erf} \left( \frac{x}{\sqrt{2}} \right) \right]


ReLUとGELU
出典：
Masaki Hayashi, GELU (Gaussian Error Linear Unit) Transformer系モデルでよく使用, @CVMLエキスパートガイド, https://cvml-expertguide.net/terms/dl/layers/activation-function/relu-like-activation/gelu/

ReLUとGELUの比較

項目 ReLU GELU
滑らかさ 不連続（0かx） なめらか（確率的に値を通す）
勾配消失 起きにくいが、x<0で勾配0 より安定（勾配は常に非ゼロ）
出力範囲 [0, \infty) 負の値も含む（なだらかに0に近づく）
実行コスト 低い（単純なmax） 高い（erfやtanhを使う）
学習の安定性 やや不安定 安定しやすい
GitHubで編集を提案

Discussion