Zenn
✅

ニューラルネットワーク

に公開
学習記録
ニューラルネットワーク
idea

はじめに

概要

  • シラバス：E資格2024#2
  • ニューラルネットワークの全体的なイメージを掴みます

キーワード

ニューラルネットワーク, 勾配消失, 活性化関数, 万能近似定理,
全結合層, 重み, バイアス

学習内容

モデル訓練のステップ

  1. アーキテクチャの設計
  2. 入力層設計
    • データの前処理
    • ノード数を決める
  3. 中間層設計
    • 活性化関数
    • 隠れ層を決める
  4. 出力層設計
    • 出力ユニット
  5. 誤差計算
  6. モデルに誤差を反映する
  7. 重みの更新の設定をする
  8. 最適なモデルを手に入れる

ニューラルネットワークの構造


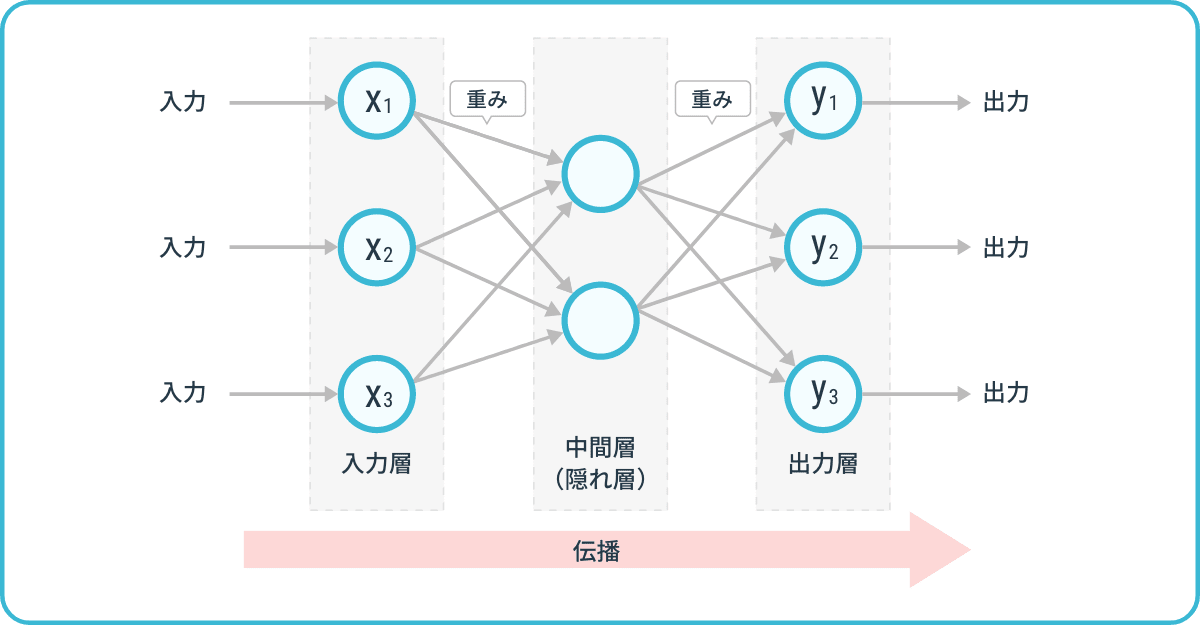
出典：
AIsmiley編集部, ニューラルネットワークとは？仕組みや歴史からAIとの関連性も解説(2024), https://aismiley.co.jp/ai_news/neural-network/

  • 入力層：学習や推論に使用する情報を取り込みます。入力データの次元数(特徴量の数)がノード数になります
  • 中間層（隠れ層）：特徴抽出の役割を持っています
    • ノード数を増やしすぎると学習に時間がかかりますが、ノードが少ないと十分な学習がされないことがあります
    • 隠れ層の数を増やすと、表現力が高くなりますが、層が深くなればなるほど、勾配消失問題や過学習になりやすくなります
    • 学習可能なパラメータ（重みやバイアス）を設定します
  • 出力層：適切な活性化関数を使って、出力の意味（確率、スコア、連続値など）を整えます
    • 問題の種類（分類/回帰など）に応じてノード数が変わる

勾配消失

  • 勾配(重みの更新量)が極端に小さくなり学習が進まなくなります
  • 勾配消失＝重みが更新されない → 学習が止まる

活性化関数

  • 活性化関数を使うメリットは、複雑な計算をすることができる点です


出典：
https://taketake2.com/N57.html, パーセプトロンとは(2019), https://taketake2.com/N57.html

画像のように、入力データを活性化関数を使うと、より複雑な計算をできます

全結合層（fully connected layer / dense layer）

  • 前層のすべてのノードと接続されます
  • 主に隠れ層や出力層で使われます
  • 表現力が高いが、パラメータ数が多く過学習しやすいです

Step1: アーキテクチャの設計

  • 層やノードの数が多いほどいいというわけではなく、最適な個数を決めることが重要です


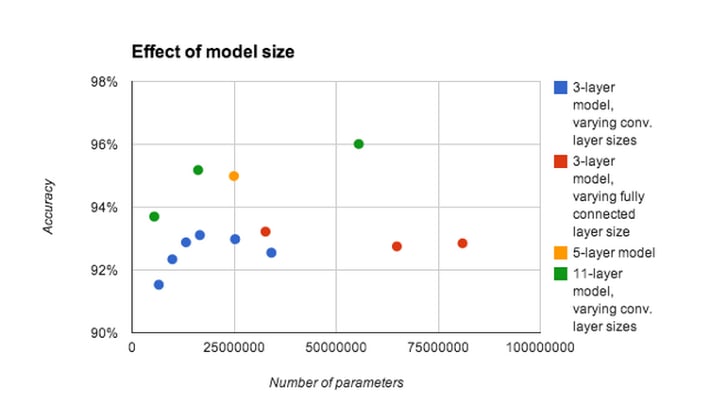
出典：
Julian Ibarz, Ian J. Goodfellow et. ac, Multi-digit Number Recognition from Street View Imagery using Deep Convolutional Neural Networks(2024),ICLR 2014 conference

  • 縦軸：予測の正確率
  • 横軸：使用するパラメータ数
  • 赤点、青点：3層モデル
  • オレンジ色：5層モデル
  • 緑色：11層モデル

3層モデルを注目します。パラメータ数多いほど正確率が高くなるではありません。
また、画像から見るとモデルの層が多い方が正確率が高くになるが、使用するリソース（時間や機器性能など）も考慮するが必要です

万能近似定理（Universal Approximation Theorem）

  • ニューラルネットワークが理論的に何でも学習できるポテンシャルがあることを示します
  • 学習の難しさ、データ、計算資源など現実の制約は依然として存在します
観点 万能近似定理 実用上の現実
層の数 1層でも可能 実際は多層の方が効率的
ノード数 無限に増やせばよい リソースや学習効率が問題になる
活性化関数 任意の非線形関数でOK 実用ではReLUが主流
精度 任意の精度で近似可能 学習データ、オーバーフィッティングなど現実的制約あり

重み(weight)とバイアス (bias)

用語 説明
重み 入力の重要度を示す係数
バイアス 出力のオフセットを調整する定数項
共通点 学習によって最適化されるパラメータ
違い 重みは入力にかかる、バイアスは出力に加えられる
  • 例：z=w_1x_1+w_2x_2+\cdots +w_nx_n+b
    • w：重み
    • b：バイアス
GitHubで編集を提案

Discussion