✅
機械学習の課題
はじめに
概要
- シラバス:E資格2024#2
- 機械学習の課題と解決策を知ります
- 機械学習の解決策を考える場合に、バランスが重要です。やりすぎると反対的な課題が出ます。
キーワード
汎化性能, 汎化誤差, 訓練誤差, バイアス, バリアンス,
過学習, 次元の呪い, 過剰適合, 過少適合, 正則化
学習内容
汎化性能(Generalization Performance)
- AIモデルが、学習に使っていない新しいデータに対しても、正確に予測や判断ができる能力のことです
汎化性能が高い:新しいデータにも強い
汎化性能が低い:学習データだけでしか通用しない(=過学習)
汎化誤差(Generalization Error)
- 未知のデータに対する間違いの度合い
- 未知のすべてのデータに対する平均的な誤差
- AIモデルは訓練データでは高精度でも、初めて見るデータに弱いことがあります。それを測るのが汎化誤差です
- 汎化誤差の値が小さいほど、応用が効きます
テスト誤差
- 学習後に手元にあるテストデータで測った誤差です
- テストデータを使いすぎると汎化誤差を正しく測れなくなります(情報漏れ)
訓練誤差
- 学習に使ったデータに対する誤差です
汎化性能を測る方法
- テストデータで評価する(学習に使ってないデータ)
- 交差検証(クロスバリデーション)を行う
- 汎化誤差を見る(テスト誤差 ≒ 汎化誤差)
汎化性能を高めるには
| 方法 | 内容 |
|---|---|
| 十分なデータ量 + 多様なデータ | データが少ないと偏るため、多くて多様なデータを用意 |
| 適切なモデル選択 | 複雑すぎると過学習、単純すぎると表現力不足 |
| 正則化 | 不要な重みを抑えることで過学習を防ぐ |
| データ拡張 | 画像やテキストのバリエーションを増やして訓練する |
| ドロップアウト(深層学習) | ニューラルネットの一部を一時的に無効にして学習 |
バイアス(Bias)とバリアンス(Variance)
- バイアスとバリアンスはトレードオフの関係にあり、どちらか一方を減らすと、もう一方が増える傾向があります
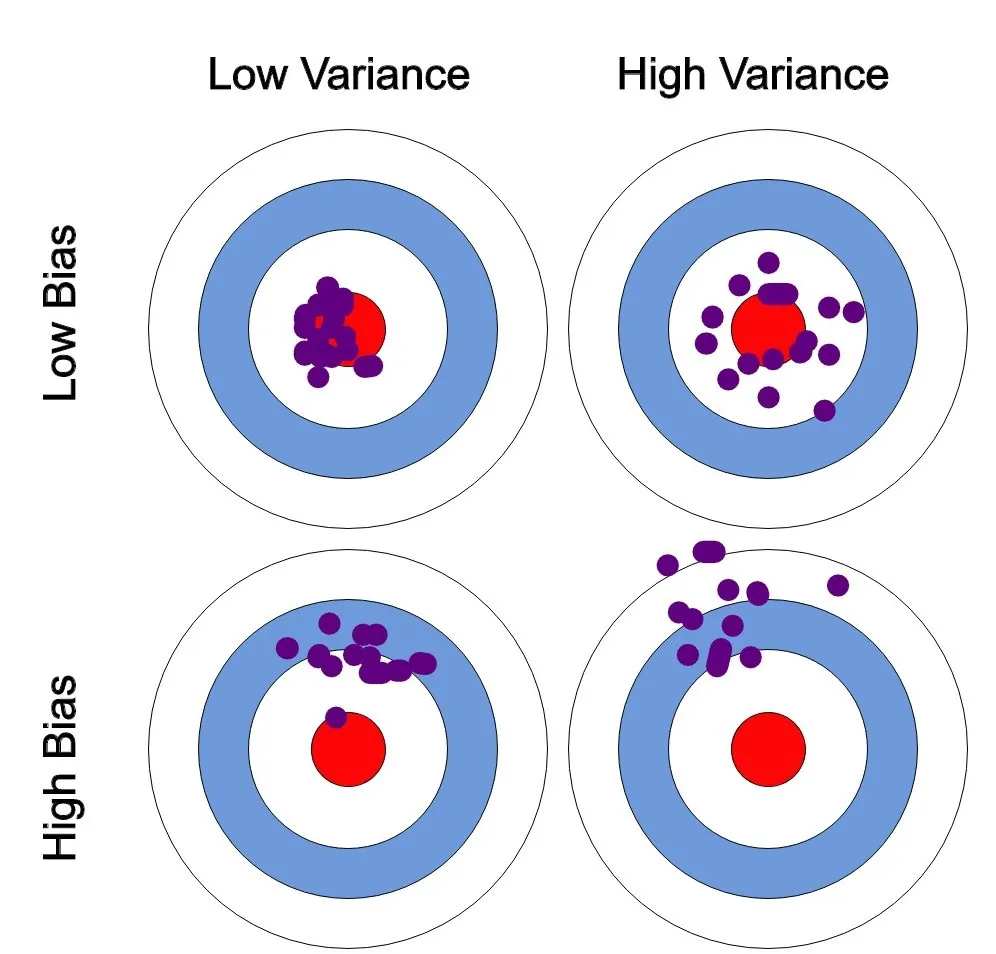
出典:
Varun Bhatia, Bias and variance using bulls-eye diagram, Bias & Variance- The Ultimate Trade-Off(2021), https://medium.com/analytics-vidhya/bias-variance-the-ultimate-trade-off-e604528bd30a
- 左上(バイアスが低い、バリアンス低い):中心にヒットします
- 右上(バイアスが低い、バリアンス高い):中心の周りに散らばっています
- 左下(バイアスが高い、バリアンス低い):中心に外れたところで集中しています
- 右下(バイアスが高い、バリアンス高い):あっちこっちで散らばっていて、規則性がない感じです
バイアス
-
モデルの予測が真の値からどれだけずれているかを示します
-
過少適合の原因となります
-
高バイアスの場合
- モデルが単純すぎてデータのパターンをうまく捉えられません
- 訓練データにもテストデータにも精度が悪いです
-
低バイアスの場合
- モデルが不安定になる:新しいデータに対して大きく出力が変動する
- テスト誤差が大きくなる:学習データではうまくいっても、未知のデータに対しての精度が著しく低くなります
- 過学習しやすい:訓練データに完璧にフィットしすぎることで、テストデータでは精度が落ちます
バリアンス
-
モデルが訓練データに対してどれだけ敏感に反応するかを示します
-
過学習の原因となります
-
高バリアンスの場合
- 訓練データに対して非常に高精度な予測をするが、テストデータにはうまく適応できません
- モデルが訓練データの細かなパターン(ノイズなど)にまで適応してしまいます
-
低バリアンスの場合
- モデルが単純すぎて、データのパターンを捉えられません
- 訓練誤差もテスト誤差も高くなって、モデルが「何も学べていない」状態です
- 予測が大雑把で精度が低くって、入力が多少変わっても、出力が変わらず、使い物にならないです
過学習(Overfitting)
- 訓練データに依存しすぎ、未知のデータに対してうまく対応できなくなる状態のことです
- 汎化性能が低下します
- 過剰適合(Overfitting)とほぼ同じ意味です
- 過剰適合は学術論文や統計的な分析の用語・現象の記述で使われやすいです
- 英語の表記は同じです
特徴
| 特徴 | 説明 |
|---|---|
| 訓練誤差がとても低い | 学習データに対しては完璧に近い予測をする |
| テスト誤差が高い | 新しいデータに対して精度が悪い |
| ノイズまで覚える | 本質ではない細かな情報・例外まで暗記してしまう |
発生原因
| 原因 | 説明 |
|---|---|
| モデルが複雑すぎる | ニューラルネットが深すぎたり、パラメータが多すぎる |
| データが少ない | 偶然の特徴に引っ張られやすい |
| 学習しすぎ | 学習回数(エポック数)が多すぎて細部まで覚えてしまう |
| ノイズが多い | 例外的なデータに引っ張られてしまう |
対策
| 方法 | 説明 |
|---|---|
| データを増やす | 多様なパターンを学習させる |
| 正則化(L1/L2) | パラメータが無駄に大きくならないよう制限する |
| ドロップアウト | ニューラルネットの一部を無効にして汎化力を上げる |
| 早期終了(Early Stopping) | テスト誤差が増えた時点で学習を止める |
| モデルの簡略化 | 小さめのネットワークを使う、不要な特徴量を除く |
| クロスバリデーション | 過学習を検知するためのテスト方法 |
次元の呪い(Curse of Dimensionality)
- データの次元数が増えると、学習の難易度が急激に上がる現象を指します
発生原因
- 次元が増えると、データの特徴空間が指数関数的に広がります。また、下記の問題が発生します
- データが疎になる:高次元空間では、データ点同士が遠く離れた位置に存在することが多くなります。その結果、有意義なパターンを見つけるのが難しくなります
- 計算コストが急増:必要な計算リソース(メモリや処理速度)が急激に増えます
- 過学習のリスクが高まります:モデルがデータの細部(ノイズ)まで覚えてしまうことがあり、過学習のリスクが高くなります
- 次元間の相関の低下:次元数が増えると、特徴量間の相関性が薄くなるため、重要な情報をうまく捉えきれないことが増えます
対策
- 特徴選択(Feature Selection):不要な特徴量を削除して、モデルが学習するべき重要な特徴に絞り込む方法です
- 主成分分析(PCA):高次元のデータを低次元空間に変換する手法です
- t-SNE(t-Distributed Stochastic Neighbor Embedding):次元削減手法の一つで、データ点を低次元空間にマッピングします
- 正則化:高次元データに対して、過学習を防ぐために、モデルの複雑さを制限する手法です
- カーネル法(Kernel Methods):特に非線形なデータに対して、カーネル法を使って高次元空間にマッピングし、線形的に分離できるようにする方法です
過少適合(Underfitting)
- AIモデルが訓練データすらうまく学習できていない状態を指します
特徴
| 特徴 | 説明 |
|---|---|
| 訓練誤差が高い | 学習したデータでもミスが多い |
| テスト誤差も高い | 本番用のデータにも弱い |
| モデルがシンプルすぎる | データの複雑さに対して表現力が足りない |
発生原因
- モデルが単純すぎる
- 学習不足
- 特徴量が不十分:入力データに必要な情報が欠けています
- 正則化が強すぎる:学習を抑えすぎて、特徴を捉えられません
解決策
- モデルを複雑にします
- 学習を長く行います
- 特徴量エンジニアリング:新しい入力変数を作成して追加します
- 正則化を弱める:学習制限を緩めてみます
正則化(Regularization)
- モデルの複雑さを抑えるために、不要な学習を抑制する手法です
- 目的
- 過学習を防ぐ
- 汎化能力を高める
- モデルは重要な特徴を優先的に学習し、無関係な特徴量に過度に依存しないようになります
正則化の方法
| 用語 | 意味 |
|---|---|
| L1 正則化 | 特徴選択を促し、不要な重みをゼロにする |
| L2 正則化 | 重みを小さく保ち、極端な値を防ぐ |
| Elastic Net | L1とL2を組み合わせて、両方の利点を活かす |
Discussion