Zenn
✅

距離計算

に公開
機械学習
学習記録
idea

はじめに

概要

  • シラバス：E資格2024#2
  • 距離計算の数式を知ります

キーワード

コサイン距離, コサイン類似度, ユークリッド距離, マンハッタン距離,
マハラノビス距離, Lp距離

学習内容

コサイン距離とコサイン類似度

  • コサイン類似度：2つのベクトルがどれだけ似ているかを測定するために使用される指標
  • 数式：

\vec{A}=(a_1,a_2); \vec{B}=(b_1,b_2)

Cosine Similarity(\vec{A},\vec{B}) = \frac{\vec{A} \cdot \vec{B}}{\|\vec{A}\| \cdot \|\vec{B}\|}=\frac{a_1a_2+b_1b_2}{\sqrt{a_1^2+b_1^2}\cdot \sqrt{a_2^2+b_2^2}}

\vec{A} \cdot \vec{B}：AとBの内積
\|\vec{A}\| , \|\vec{B}\|：AとBのノルム（ベクトルの大きさ）

  • 特徴
    • 0に近いほど似ている（類似度が高い）
    • 1に近いほど異なる（類似度が低い）
    • ベクトルのスケール（大きさ）には影響されず、向きの違いだけで距離を測定
    • 値の範囲は-1~1


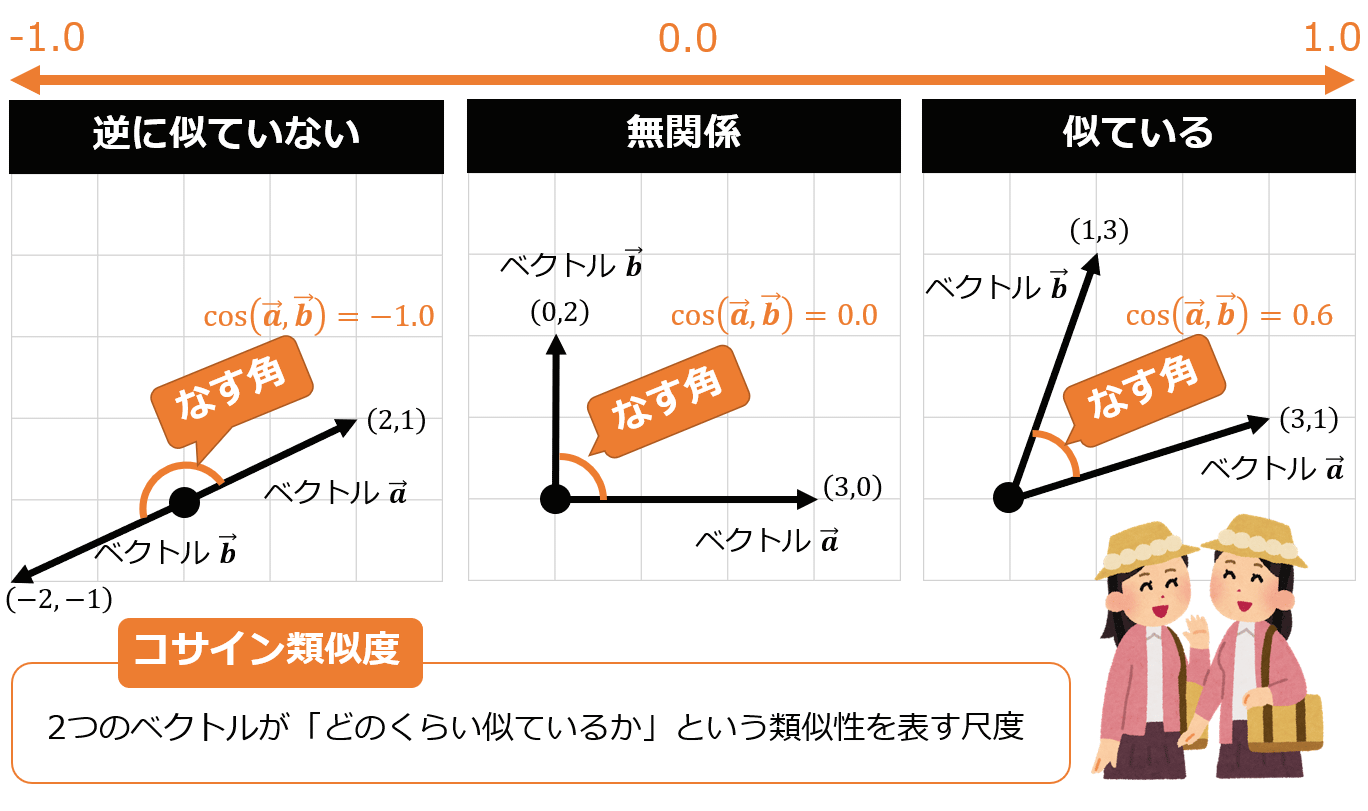
出典：@IT, コサイン類似度のイメージ, コサイン類似度（Cosine Similarity）とは？(2024), https://atmarkit.itmedia.co.jp/ait/articles/2112/08/news020.html

  • コサイン距離：2つのベクトル間の角度のコサインを用いて計算される距離指標です
  • 数式：1-Cosine Similarity
  • 特徴：
    • 値の範囲は0~2

コサイン類似度とコサイン距離 の比較

項目 コサイン類似度 コサイン距離
数式 \cos(A,B) = \frac{A \cdot B}{|A||B|} 1 - \text{Cosine Similarity}
値の範囲 -1〜1 0〜2
意味 値が大きいほど似ている 値が小さいほど似ている
用途 「どれくらい似てるか」知りたいとき 距離として使いたいとき（例えばクラスタリング、最近傍探索）

ユークリッド距離

  • 両点の間の「直線距離」
  • ピタゴラスの定理の公式で計算します
  • L2ノルムとも呼ばれます
  • 数式：d^2=a^2+b^2

マンハッタン距離

  • 点xから点yまでの距離を求める際に、座標の差（の絶対値）の総和を2点間の距離とする指標です
  • L1ノルム、タクシー距離（Taxicab Distance）とも呼ばれます
  • 数式：d(x,y) = \sum_{i=1}^{n} |x_i - y_i|

ユークリッド距離とマンハッタン距離の比較

距離の種類 計算方法 特徴
ユークリッド距離 直線距離（ピタゴラスの定理） 最短距離、L2ノルム
マンハッタン距離 縦+横の距離（絶対値の和） L1ノルム、直角移動の総距離


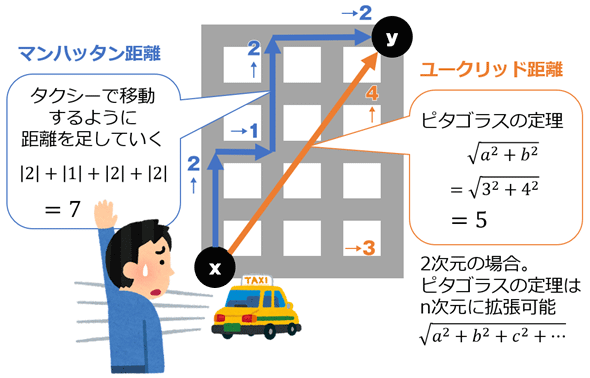
出典：@IT, マンハッタン距離／ユークリッド距離のイメージ, マンハッタン距離（Taxicab distance）／ユークリッド距離（Euclidean distance）、L1／L2ノルムとは？(2024), https://atmarkit.itmedia.co.jp/ait/articles/2111/10/news023.html

マハラノビス距離

  • データの外れ具合を定量化する指標です
    • 仮にユークリッド距離が同じでも、点の位置が異なるので、分布からの外れ具合（分散）も違いますので、マハラノビス距離が異なります

この画像を参考してください

出典：yutera12(tera), マハラノビス距離を徹底解説(2022), https://qiita.com/yutera12/items/db425fafce2d87a25a1f

  • 数式：D_M(\vec{x}, \vec{\mu}) = \sqrt{(\vec{x} - \vec{\mu})^T \, \Sigma^{-1} \, (\vec{x} - \vec{\mu})}
    • \vec{x}：対象のデータ点（ベクトル）
    • \vec{\mu}：平均ベクトル（分布の中心）
    • \Sigma^{-1}：共分散行列の逆行列
    • T：行列の転置

Lp距離

  • 一般化された距離（ノルム）を表します
  • 2点間の差の絶対値をp乗した和を1/p乗した距離
  • p=1：マンハッタン距離(L1ノルム)
  • p=2：ユークリッド距離(L2ノルム)
d(\vec{x}, \vec{y}) = \left( \sum_{i=1}^{n} |x_i - y_i|^p \right)^{\frac{1}{p}}
GitHubで編集を提案

Discussion