バイアスを取り除いた効果検証 ~傾向スコア~
この記事は「Wantedly 新卒 Advent Calendar 2021」の20日目の記事です。
今回はセレクションバイアスがある状況下での分析を傾向スコアを用いて行う話をしたいと思います。ちょっと数学チックな理論よりのお話です。この話は「効果検証入門 正しい比較のための因果推論/計量経済学の基礎」を読んで得た学びをアウトプットした結果です。
前回の復習
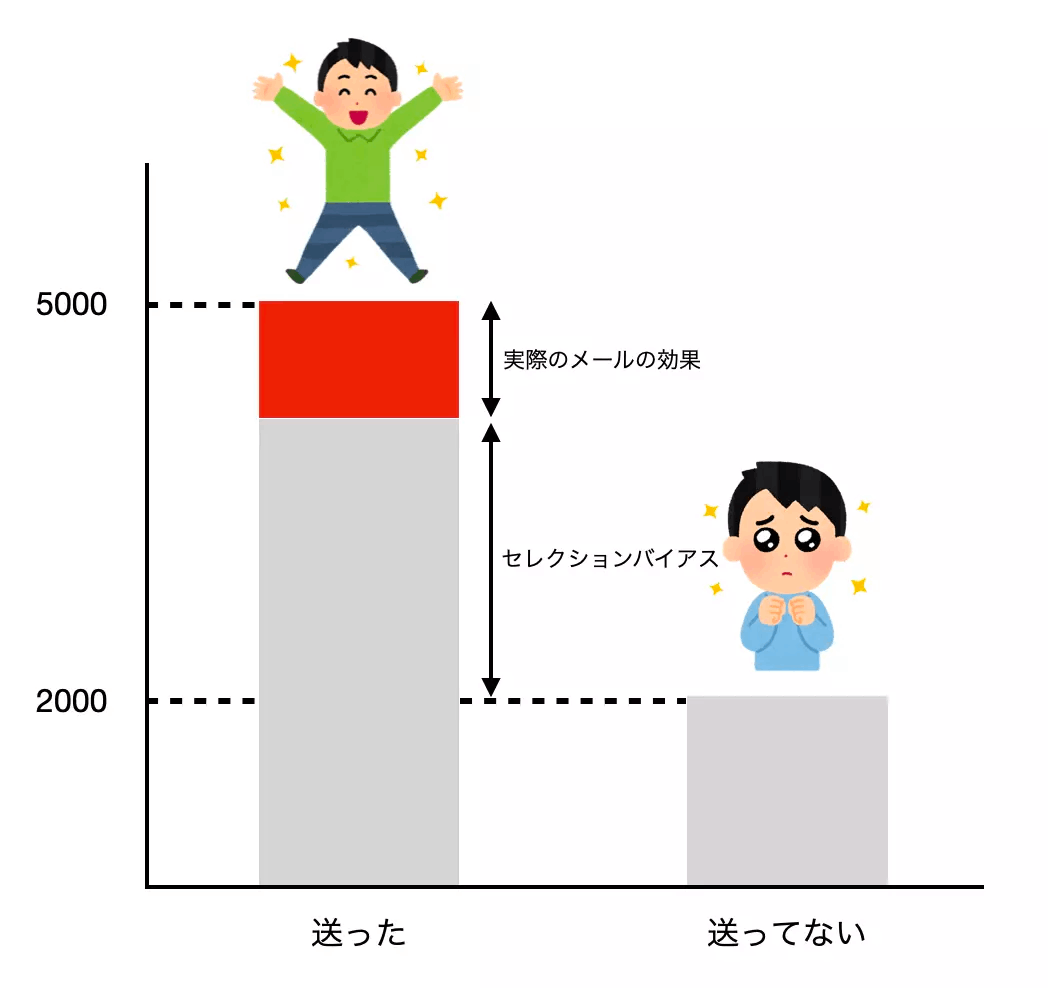
前回の自分の番で「俺たちのメールは本当に効果があったのか」という強いタイトルのもと、セレクションバイアスとは何なのかを説明しました。
セレクションバイアスはあらゆるビジネス施策で入ってくる可能性があります。その中で如何にバイアスの影響を小さくするのかは効果を分析するときに重要になります。前回の記事ではRCT(Randomized Control Trial)によってセレクションバイアスを理論上0にできると説明しました。しかし、毎回その分析のためにRCTをするわけにはいきません。キャンペーンメールを送るとしてその分析のために半分のユーザーに送るのを諦めるのはビジネス上大きな決断となります。そう、RCTは施策の介入されない方の機会損失が大きすぎるのです。このRCT自体のビジネス上のリスクから、セレクションバイアスを含んだ状態で施策を打ち、分析を迫れることが多いと思います。
セレクションバイアスの影響を減らす
では、どのようにセレクションバイアスの影響をなくすのでしょうか。結論から言うと、完全に0にするのは難しいです。影響を小さくすることしかできません。小さくするための手法はいくつかありますが、主に用いられる方法は回帰分析です。回帰分析ではバイアスに影響を与えそうな変数の傾向が同じであれば、それらの比較はセレクションバイアスが軽減された状態と考えてより正しい効果検証を行う方法です。回帰分析はそのモデリングさえしっかりしていれば、ツールもたくさん世の中にありますし、手軽に分析を行うことができます。
しかし、このバイアスに影響を与えそうな変数(共変量) を選定する作業が大変なのです。ある程度の規模になるとユーザーに関するデータの量は莫大なものとなります。それらの全てを変数として適切かどうか判断するのはとてもできる作業ではありません。また、これらの変数から予測するのは購買量だったり、何かしらを達成したかの2値など、何が影響しているかわかりづらいものになりがちです。もちろんデータとしてとれてないものの影響も考えられます。また、考えられそうな変数を全部つっこむということもできません。計算量の話もありますし、変数の多重共線性[1]にも気をつける必要があります。このような状況で適切にバイアスに関係ある変数を選択するのは至難の技です。もちろん、この壁さえ越してしまえば回帰分析はセレクションバイアスを取り除く強力な手段となります。しかし、その壁が実際の現場では高いものになってしまいます。
傾向スコア
回帰分析で変数の選択が大変という問題を解決するのが傾向スコア(propensity score)です。傾向スコアの定義は「あるサンプルにおける介入が行われた確率」です。先のメールの例で言うと、反応がよい人達に送ったとして、同じくらい反応が良い母集団の中でその人がどれくらいの確率でメールを送られたかを表しています。回帰分析では共変量の傾向が同じサンプルが介入に対して独立と考えたのに対して、傾向スコアが同じサンプルが介入に対して独立と考えます。この場合共変量が違くても傾向スコアが同じ値になることがあるので、傾向スコアを用いた分析は回帰分析を少しゆるくしたような分析になります。これは介入に対して独立な状態を共変量というベクトルから傾向スコアというスカラー値にすることで状態の表現能力を抑えたとも言えます。
傾向スコアの推定
回帰分析が目的変数を介入に対する効果としているのに対して、傾向スコアのモデルでは目的変数を介入したかどうかとします。目的変数とは今から作成するモデルにおいて予測する変数のことです。また、入力として与えられる変数(説明変数)
モデルは多くの場合ロジスティック回帰が選定されます。ロジスティック回帰は多変量の説明変数を入力にして目的変数
ただし、

ここではロジスティック回帰のみ紹介しましたが、実際には他のモデルを使うことがあります。GBDT(Gradient Boosting Desition Tree)などは大量の説明変数をつっこんだとしてもそれに耐えられるかつどの変数が作用したかどうかを意識しなくても十分な推定能力が得られます。ただし、ここでの推定能力の向上が効果検証の精度を高めることの保証にはならないため、現実的に扱いやすい手法を選ぶことになることが多いです。[2]
傾向スコアを使った推定
ここまでで傾向スコアを算出することができました。本当にやりたいことは傾向スコアを使ってセレクションバイアスの影響がすくなる効果検証です。ここからは大きく2つある効果検証を紹介していきます。その2つは傾向スコアマッチングとIPWと呼ばれるものです。
傾向スコアマッチング
傾向スコアマッチングは最初に言っていた、傾向スコアが同じサンプルは介入したかどうかと独立という性質に着目したものです。つまり傾向スコアが同じサンプルが2つあった場合、それらに対して介入をおこなったかどうかは完全にランダムになります。もしその2つが介入が行われたものと行われてないものであったらその2つの比較はセレクションバイアスを除いた本当の効果に等しいものとなります。実際には介入したサンプルの中から1つ選び、その傾向スコアと似たような傾向スコアをもつサンプルを介入が行われなかったグループから取り出し、その効果の差を求めます。それらを介入が行われたサンプル全てに行い、差の平均がセレクションバイアスの影響が少ない本来求めたかった効果となります。
この場合、介入が行われたグループからサンプルを選んでマッチングを行うので、もし介入が行われたグループが行われなかったグループよりサンプル数が多かったらいくつかの行われなかったグループのサンプルは使われないまま分析がなされることに注意してください。つまりこの分析は介入が行われたグループに対する効果検証となるのです。
マッチングはシンプルなロジックである一方でマッチする相手を探すという部分で多くの計算が必要になってしまいます。また、傾向スコアも連続した値であるため、全く同じスコアとなることはまれです。その中で一番近いものはどれかを探すのは結構な手間が必要になります。
IPW
マッチングの他にもう一つ傾向スコアを使った効果検証としてIPW(Inverse Probability Weighting)があります。IPWでは傾向スコアをそのサンプルに対する重みとして、全体の母集団に対する効果を推定します。
前回に書いた内容ですが、与えられたデータに対してある意図を持って介入の対象を選んだことによってセレクションバイアスが発生すると説明しました。つまり与えられたデータ全てに対して介入を行い効果を観測し、タイムスリップして介入前に戻って今度は介入せずに効果を観測してその差分をとればセレクションバイアスは発生せず本当の効果の差を測ることができます。しかし、このようなことは現実問題できません。
傾向スコアの定義は「あるサンプルにおける介入が行われた確率」でした。例えば傾向スコアが0.6のサンプルが10個あるとします。このとき、そのうちの6つが介入されたと考えれます。このとき、観測されるのは介入がなされた6つの効果
厳密にはこれは観測できないので計算できません。しかし、傾向スコアの逆数を使うことで擬似的に上の式の計算ができます。これは実際には6つの
ちょっとゴツい式になってしまいましたが、これで全体の母集団での平均の効果の差分を推定できました。IPWではマッチングと違って計算量の問題はありません。
まとめ
今回はセレクションバイアスを取り除くような分析手法として、回帰分析と比較しながら傾向スコアを紹介しました。また、そのモデルのあり方とモデルを用いた効果検証の考え方をマッチングとIPWの2つ紹介しました。これらはRやsckit-learnを用いて簡単に分析できるのでぜひ普段からの分析に用いてみてはいかがでしょうか。これまで見てきた感じ、間違ったバイアスのループに入らないように普段からセレクションバイアスを含むかどうかを考えながら分析するのは難しいですが、やっていき💪という感じですね!
Discussion