数学記号がわからないならプログラムを書けばいいじゃない。

とある数学（というか数字）嫌いマンの伝説

• 数IIIと数Cをなんとなくのコレクション精神で履修してみるも、何もかも意味がわからない
• 原因をたどったらそもそも数Iあたりから既によくわかっていなかった
• 飲み会に行くと割り勘の計算ができない
• むしろ1000円上乗せぐらいならあげるからよしなにやっといてという気持ち
• なぜかプログラムは一般人レベルぐらいには書ける

で、なんで今更？

• なんか分析とかやってみたいの！かっこよさそうじゃん？
• 最終的には未来を予測してこの世界の神になるんじゃ！

というわけで神を目指す数学嫌いマンは着々と数学の復習をしていったわけですが....。
数学記号あるじゃないですか。なんすか、あれ。知らんし。

そこで思いついたのです。
数学記号がよくわからないならプログラムで実装してみたら良いのでは、と。

Σを実装してみる

とりあえず手始めにΣの意味を忘れてしまったので、自分で実装してみることにしました。
※本記事はわからない人がわからないなりに理解しようとした内容のため、用語等が正確でない場合があります

そもそもΣの目的とは

目的が不明確だと勉強しても全くしっくり来ませんね。
Σの意味は総和、つまり数の一覧（配列）を作成して合計値を求めることです。

たとえば[1,2,3,4,5,6,7,8,9,10]の合計値は55ですが、この合計値を一文字で書き表すために使う記号ということになるでしょう。いや、わかりますよ。でもそれなら1～10までの合計って書けばいいじゃん。

では仮に数の一覧が[2,4,6,8,10]だったら。「1～10の中の偶数値のみの合計」となるでしょうけれど、長い。条件が複雑化すればするほど読みにくくなるらしいです。個人的には文章化してくれたほうが読みやすいんですけどね。

ともかくここでΣが登場します。

##Σは繰り返し処理である
たとえば、[1,2,3,4,5,6,7,8,9,10]の合計値はこのように表すことができます。

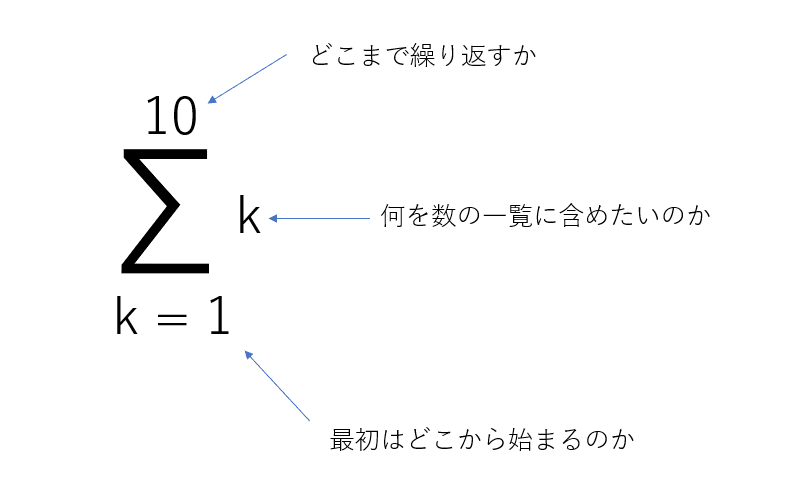
つまり、1から10まで繰り返しながら、繰り返し毎に1から10までの値をそのまま配列に追加して行き、最後に配列内の全要素の合計を求めるという意味になります。
私の場合は合計をいきなり求めようとするとアレルギー反応を起こしますので、まずは落ち着いて先に数列を作ります。というわけで1~10までの配列（リスト）をpythonで実装してみます。

array = []
for i in range(1, 11):
  array.append(i)

うん、全然問題ないですね。
あとは合計値を求めるのであれば、

sum(array)
 # => 55

と書けば合計値が求まるはずです。

コードに落とすと余裕なのにΣだと一瞬意味不明に見える。
これは数学記号が格好つけて可読性の低い記号や文字を使っているからです。
本当は多分由来とかあるんだと思います....。
ではこの一般的なpythonコードとΣ記号の差を埋めていきましょう。

同じ役割を持つ変数や値を色分けしてみました。
これで多少はわかりやすくなります。「どこまで繰り返すか」はrange()関数の仕様上11になりますが仕方ないです。

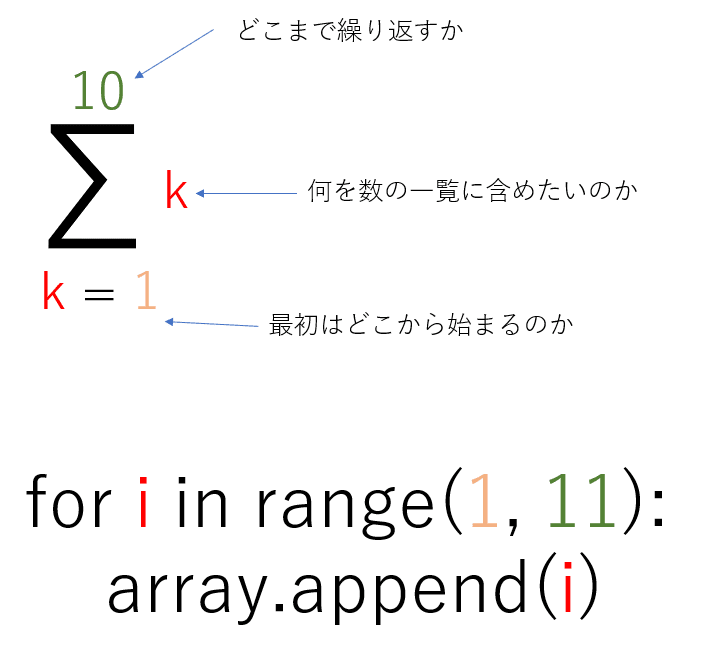
この場合だと、kとiは同じ役割を担っていますね。
どうせなら変数名は統一しましょう。

array = []
for k in range(1, 11):
  array.append(k)

これで少しわかりやすくなりました。

こころのこえ

kとかnとかaとか使わずに"start_from"とか"end"とか"element"とかわかりやすい変数名にしてくれたらいいのにな。そもそもΣ自体、英語で総和を表す"Summation"のSをギリシャ文字のΣにしたものらしいですよ。じゃあSummationでいいじゃん。なんで略すのよ。そもそもsummationの語源ってラテン語だからね？なんでギリシャ文字にするのよ。かっこいいけどさ！

処理部分のカスタマイズ

さて話を戻します。
Σの右側が先程は"k"と書いてありましたが、このようにまた別の式が入ってくることもあります。

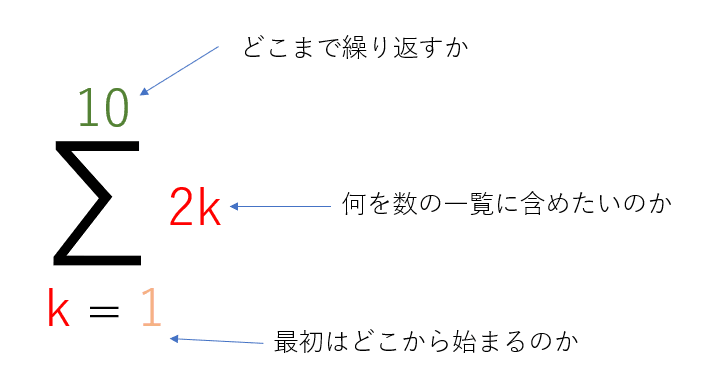
これは、コードにすれば非常にシンプルです。
最終的にリストに含めたい値がどのように加工されるのかを示していると考えると良いでしょう。

array = []
for k in range(1, 11):
  array.append(k) #ここのkの部分に当たる

ですので、今回の例であれば

array = []
for k in range(1, 11):
  array.append(2 * k) 

このように書けるわけです。

非常にシンプルな式しか扱っていませんが、あとはこれの応用でいけるのではないでしょうか。

ちょっと遊んでみる（おまけ）

さて、基礎はわかったのでプログラム的な視点で調整してみようと思います。
まず、毎回書くのは面倒なので関数化してみます。

安直な関数化

安直に関数化するとこうなりますね。戻り値はちゃんと総和を返すようにしています。

def sigma():
  array = []
  for k in range(1, 11):
    array.append(2 * k)

  return sum(array)

値を外から受け取る

このままだと柔軟性に欠けるので、値はちゃんと外から受け取るようにしましょう。

def sigma(k, n):
  array = []
  for k in range(k, (n + 1)):
    array.append(2 * k)

  return sum(array)

# 関数の呼び出し例
print(sigma(1, 10))
 # => 1から10それぞれに2を掛けたものの総和なので110

式も外から受け取る

式も外から受け取れるようにしましょう。ここはラムダ式を使ってみます。

def sigma(k, n, func):
  array = []
  for k in range(k, (n + 1)):
    array.append(func(k, n))

  return sum(array)

#関数の呼び出し例
print(sigma(1, 10, lambda k, n : 2 * k))
 # => 1から10それぞれに2を掛けたものの総和なので110

ここで察しました。
あれ、リスト内包表記ってもしかして....

##リスト内包表記の場合

array = [2 * k for k in range(1, 11)]
print(sum(array))

なるほど.....。

print(sum([2 * k for k in range(1, 11)]))

なんと1行にまで縮まりました。
実行速度が早いとかは知ってましたが、リスト内包表記ってこういう意味でも楽なんですね。
なんならこのあと条件分岐とかも挟めますし！

結論

プログラムが書けるけど数学ができない人はプログラムを書いてみるのも手かもしれません！
Σが便利だとは思いませんでしたが、少なくとも理解はできましたしリスト内包表記が素晴らしいことはわかりました（笑）。