QiskitでQRAM付きのQuantum Countingを実装する方法
すでに量子計算の資料がかなりネット上に充実してきているので、quantum countingの実装はたくさん乗っていると思いますが、最近諸事情で改めてスクラッチで実装する機会があったので、僕なりの実装方法を共有します。
概要
今回は、Quantum Countingを使って「ステップbyステップで2つの選択肢から1つ選ぶ際に、選択した値の和がある定数以上の選択方法の数を数える」量子回路を実装します。
問題設定の具体的な状況としては、以下のような感じです。
list0 = [1,3,5,7]
list1 = [8,6,4,2]
list0, list1の対応するインデックスについて、いずれか一方から1つずつ選んで長さ4の新しいlistを作るとします
ステップ1: list0を選ぶ -> list0[0]を選択
ステップ2: list1を選ぶ -> list1[1]を選択
ステップ3: list1を選ぶ -> list1[2]を選択
ステップ4: list0を選ぶ -> list0[3]を選択
とすると、選び方は"0110"のように記述され、[1,6,4,7]のようなリストが作られます。
このリストの和は18になります。
このような選び方の全体は通りあります。 2^4 = 16
一方、和が定数C=22より大きいような選び方は、"1100", "1110", "1011"の3通りのみです。
Quantum Countingについては、Qiskit Textbookの解説が割とわかりやすいと思うので、詳細はそちらに譲ります。
(僕は最初この教材で勉強しました、一部のコードはこの記事のものを改変しています: 使用箇所は以下に明記しています。)
また、実装について、量子回路のサブルーチンはqiskit.circuit.Gateにしてから使用することで、目視での確認を楽にすることができます(特にcontrolled gateの可視化)。
Gate型で使うメリットとして、他にも元のQuantumCircuitのqubit数やqubit配置に縛られず、コード上で楽に任意のqubitに対して任意のqubitの順序で量子操作を適用できる点や、楽にinverseを作成できる点が挙げられます。
具体的な使い方は、Qiskit Docs --- ControlledGateなどが詳しいです。
下準備
とりあえず、以下のライブラリをimportしました。
from typing import Union
import numpy as np
pi = np.pi
from qiskit import Aer
from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister, execute, assemble
from qiskit.compiler import transpile
from qiskit.circuit import Gate
from qiskit.circuit.library.standard_gates import ZGate
from qiskit.circuit.library import QFT
from qiskit.visualization import plot_histogram
量子定数加算減算回路
今回は加算、減算回路を連続的に何度も使用するので、Draper による、QFTを使用した定数加算手法を採用します。
量子定数加算減算回路は"さまざまな実装方法がありますが、古典の算術演算を量子回路上の可逆回路として実装したものは、carryのためだけの量子ビットを必要とし、それに加え、多くの制御ゲートを使用しています(詳しく調べてないけど、定数加算ならもっと賢い方法でできるのかな?)。
QFT AdderはQFTを行なってから、各量子ビットの位相空間をいじり、IQFTで戻す、というアイデアに基づいています。
これだけでは大きなメリットはなさそうですが(むしろ深さが
c.f.) QFT Adderは、Pavlidis and Gizopoulosの一般化手法やRuiz-Perez and Garcia-Escartinのサーベイとかが詳しいです。
定数加算減算についての位相操作は以下のような実装になります。
# Addition by QFT
def subroutine_add_const(num_qubits: int, const: int, to_gate=True) -> Union[Gate, QuantumCircuit]:
const = const % (2 ** num_qubits)
qc = QuantumCircuit(num_qubits)
for i in range(num_qubits):
for j in range(num_qubits - i):
if const >> (num_qubits - 1 - (i + j)) & 1:
qc.p(pi / (2 ** j), i)
return qc.to_gate(label=" [+"+str(const)+"] ") if to_gate else qc
# Subtraction by QFT
def subroutine_sub_const(num_qubits: int, const: int, to_gate=True) -> Union[Gate, QuantumCircuit]:
const = const % (2 ** num_qubits)
qc = QuantumCircuit(num_qubits)
for i in range(num_qubits):
for j in range(num_qubits - i):
if const >> (num_qubits - 1 - (i + j)) & 1:
qc.p(-pi / (2 ** j), i)
return qc.to_gate(label=" [-"+str(const)+"] ") if to_gate else qc
QRAMの実装方法
QRAMへのデータのエンコードにおいて、量子ビット数の多項式時間で完了する例は組み合わせ最適化問題のエンコードによく出てきます。
まず結論を言うと、今回の例は、以下のように実装できます。
list0 = [1,3,5,7]
list1 = [8,6,4,2]
def qram_encoder(index_qubits: int, data_qubits: int, list1: list, list2: list, to_gate = True) -> Union[Gate, QuantumCircuit]:
qr = QuantumRegister(index_qubits, "index")
qr_data = QuantumRegister(data_qubits, "data")
# qr_anc = QuantumRegister(1, "ancillary")
qc = QuantumCircuit(qr, qr_data)
qc.append( QFT(len(qr_data), approximation_degree=0, do_swaps=False, inverse=False, name='QFT').to_gate(), qr_data[::-1] )
for i, (val1, val2) in enumerate(zip(list1, list2)):
qc.append(subroutine_add_const(len(qr_data), val1).control(1), qr[i:i+1] + qr_data[:])
qc.x(qr[i])
qc.append(subroutine_add_const(len(qr_data), val2).control(1), qr[i:i+1] + qr_data[:])
qc.x(qr[i])
qc.append( QFT(len(qr_data), approximation_degree=0, do_swaps=False, inverse=True, name='IQFT').to_gate(), qr_data[::-1] )
return qc.to_gate(label=" QRAM Encoder ") if to_gate else qc
これを量子回路で出力してみると、
qc_qram_encoder = qram_encoder(index_qubits, data_qubits, list0, list1, to_gate = False)
qc_qram_encoder.draw("mpl")
のようになります。(当然、最初に一様重ね合わせ状態を作ることが前提です。)
上図では、各量子ビットを、新しく作るlistの各indexにおいてlist0, list1のどちらを選択するかという情報に対応させています。
以上の回路が具体的に何をやっているかと言うと、一様重ね合わせ状態にある初期状態から、量子ビットlist0[i]を足しており、1を選ぶ場合にそのような選び方全体に対してlist1[i]を足しています。
こうすることで、
これを数式で表現すると、以下のようになります。
また、データの量子ビット数は、とりうる和の最大値の桁数をにします。
(以上の実装ではoracleの実装方法の関係で、実際には量子ビット数を1大きくしています。)
Oracle
Grover iterationのoracleとして、今回はQRAMにおいて、ある定数Cより大きい値のデータの位相を反転させるとします。
そのような印の付け方の一例として、carryに注目する方法があります。
具体的には、データの量子ビット数をdとすると、Cより大きい値のみ最上位量子ビットに1が立ちます。
たとえば、今回の場合では、QRAMは次のようにエンコードされますが、
index data 0000 010100 0001 001101 0010 010001 0011 001010 0100 010101 0101 001110 0110 010010 0111 001011 1000 011001 1001 010010 1010 010110 1011 001111 1100 011010 1101 010011 1110 010111 1111 010000
これに
index data 0000 011101 0001 010110 0010 011010 0011 010011 0100 011110 0101 010111 0110 011011 0111 010100 1000 100010 1001 011011 1010 011111 1011 011000 1100 100011 1101 011100 1110 100000 1111 011001
となり、dataの最上位ビットが1になっているindexが3つあることが確認できます。
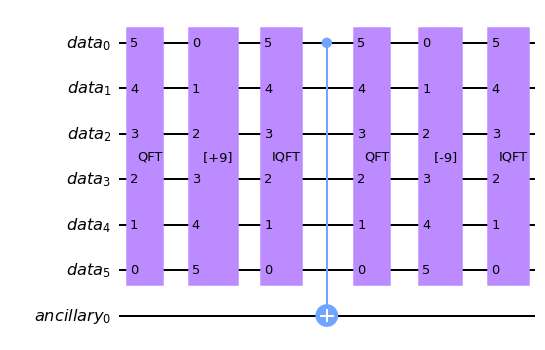
以上を実装したのが次の回路です。
def oracle(data_qubits: int, value: int, to_gate = True) -> Union[Gate, QuantumCircuit]:
qr_data = QuantumRegister(data_qubits, "data")
qr_anc = QuantumRegister(1, "ancillary")
qc = QuantumCircuit(qr_data, qr_anc)
qc.append( QFT(len(qr_data), approximation_degree=0, do_swaps=False, inverse=False, name='QFT').to_gate(), qr_data[::-1] )
qc.append(subroutine_add_const(len(qr_data), value), qr_data[:])
qc.append( QFT(len(qr_data), approximation_degree=0, do_swaps=False, inverse=True, name='IQFT').to_gate(), qr_data[::-1] )
qc.cx(qr_data[0], qr_anc)
# もし、ある定数「以下」のものに印をつけるなら、上のcxを消して次のようにすればいい。
# qc.x(qr_data[0])
# qc.cx(qr_data[0], qr_anc)
# qc.x(qr_data[0])
qc.append( QFT(len(qr_data), approximation_degree=0, do_swaps=False, inverse=False, name='QFT').to_gate(), qr_data[::-1] )
qc.append(subroutine_sub_const(len(qr_data), value), qr_data[:])
qc.append( QFT(len(qr_data), approximation_degree=0, do_swaps=False, inverse=True, name='IQFT').to_gate(), qr_data[::-1] )
return qc.to_gate(label=" Oracle ") if to_gate else qc
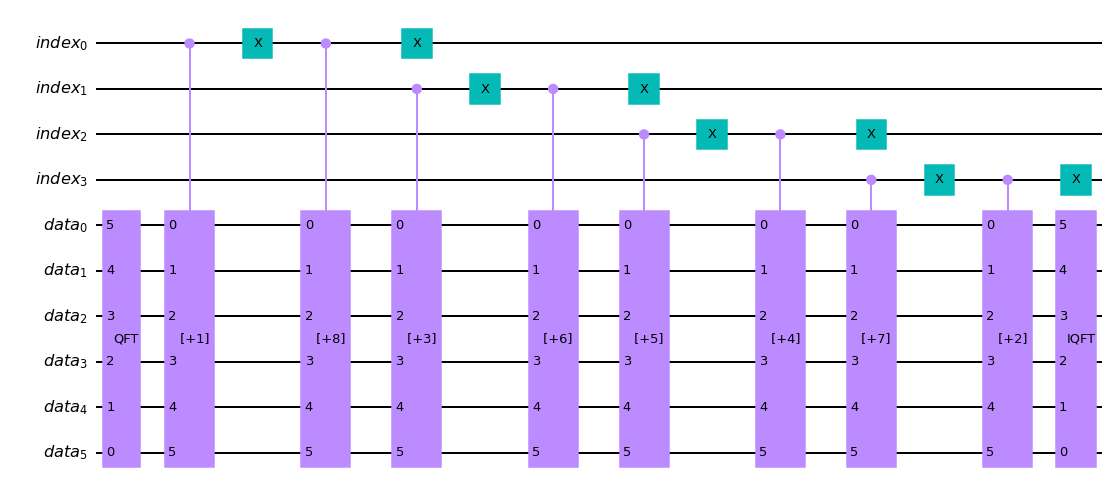
この量子回路を出力すると、
qc_oracle = oracle(index_qubits, data_qubits, C_complement, to_gate = False)
qc_oracle.draw("mpl")
のようになります。
ancillaryの部分はQRAM付きGroverでお馴染み、phase kickback用の
oracleの外でこの状態に初期化してある設定なので、ここでは最初から
実際にoracleとして使うには、エンコードしたQRAMを全て0状態に戻さなければいけないので、完全なoracleは次のようになります。
(実はqram_encoderとoracleを一つの関数にすると、使用するQFTをさらに減らせます!)
def oracle_with_encoder(index_qubits: int, data_qubits: int, list1: list, list2: list, value: int, to_gate = True) -> Union[Gate, QuantumCircuit]:
qr = QuantumRegister(index_qubits, "index")
qr_data = QuantumRegister(data_qubits, "data")
qr_anc = QuantumRegister(1, "ancillary")
qc = QuantumCircuit(qr, qr_data, qr_anc)
qc.append(qram_encoder(index_qubits, data_qubits, list1, list2), qr[:] + qr_data[:])
qc.append(oracle(data_qubits, value), qr_data[:] + qr_anc[:])
qc.append(qram_encoder(index_qubits, data_qubits, list1, list2).inverse(), qr[:] + qr_data[:])
return qc.to_gate(label=" Oracle with Encoder ") if to_gate else qc
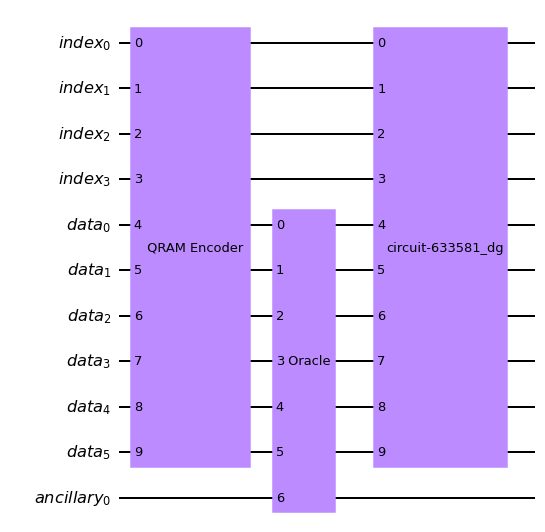
操作を反転するには、.reverse_ops()メソッドか、inverse()メソッドを使います。
qc_oracle_with_encoder = oracle_with_encoder(index_qubits, data_qubits, list0, list1, C_complement, to_gate = False)
qc_oracle_with_encoder.draw("mpl")
Diffusion
Grover iterationのdiffusionの部分は、みなさんおなじみの回路を使用します。
def diffusion(index_qubits: int, to_gate = True) -> Union[Gate, QuantumCircuit]:
qr = QuantumRegister(index_qubits, "index")
qc = QuantumCircuit(qr)
qc.h(qr)
qc.x(qr)
qc.append(ZGate().control(index_qubits - 1), qr)
qc.x(range(0, index_qubits))
qc.h(range(0, index_qubits))
return qc.to_gate(label=" Diffusion ") if to_gate else qc
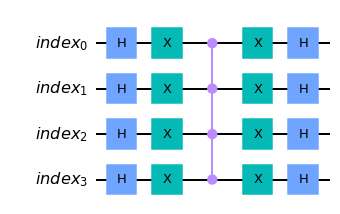
図にすると、
qc_diffusion = diffusion(index_qubits, to_gate = False)
qc_diffusion.draw("mpl")
Grover Iterator
Grover itarationは、先述のoracleとdiffusionを組み合わせ、
次のように実装できます。
def grover_iteration(index_qubits: int, data_qubits: int,
list1: list, list2: list, value: int,
to_gate = True) -> Union[Gate, QuantumCircuit]:
qr = QuantumRegister(index_qubits, "index")
qr_data = QuantumRegister(data_qubits, "data")
qr_anc = QuantumRegister(1, "ancillary")
qc = QuantumCircuit(qr, qr_data, qr_anc)
qc.append(oracle_with_encoder(index_qubits, data_qubits, list1, list2, value), qr[:] + qr_data[:] + qr_anc[:])
qc.append(diffusion(index_qubits), qr)
return qc.to_gate(label=" Grover Iteration ") if to_gate else qc
全体の初期化
関数にするほどでもないですが、一応、以下のように実装できます。
def initialization(num_qubits: int, to_gate = True) -> Union[Gate, QuantumCircuit]:
qc = QuantumCircuit(num_qubits + 1)
qc.x(num_qubits)
qc.h(range(num_qubits + 1))
return qc.to_gate(label=" Initialization ") if to_gate else qc
Quantum Countingの大枠
Quantum Countingは一言で言うと、Grover iteratorを制御ユニたりにした位相推定です。
残念ながら、ここは指数個のGrover iterationを使用してしまいます。
上手い縮約方法あるのかな...あれば教えてください m(__)m
def quantum_counting(qft_qubits: int, index_qubits: int, data_qubits: int,
list1: list, list2: list, value: int,
to_gate = True) -> Union[Gate, QuantumCircuit]:
qr_qft = QuantumRegister(qft_qubits, "qft")
qr_index = QuantumRegister(index_qubits, "index")
qr_data = QuantumRegister(data_qubits, "data")
qr_anc = QuantumRegister(1, "ancillary")
qc = QuantumCircuit(qr_qft, qr_index, qr_data, qr_anc)
qc.append(initialization(qft_qubits + index_qubits), qr_qft[:] + qr_index[:] + qr_anc[:])
iterations = 1
for i_qft in range(qft_qubits):
for i_iter in range(iterations):
qc.append(grover_iteration(index_qubits, data_qubits, list1, list2, value).control(1), qr_qft[i_qft:i_qft + 1] + qr_index[:] + qr_data[:] + qr_anc[:])
iterations *= 2
qc.append( QFT(len(qr_qft), approximation_degree=0, do_swaps=True, inverse=True, name='IQFT').to_gate(), qr_qft)
return qc.to_gate(label=" Quantum Counting ") if to_gate else qc
得られた確率分布は、以下の関数を使用して、位相から数(float)に変換します。
以下のコードはQiskit Textbookの解説の実装を多く参考にしました(ほぼ同じ)。
今回はQRAMの実装方法の解説なので、この部分の仕組みの詳細はQiskit Textbookの解説に譲ります。
# OK
def calculate_markers(measured_int, t, n):
"""
measured_int:
t : qft_qubits (number of qft qubits)
n : index_qubits (number of index qubits)
"""
# Calculate Theta
theta = (measured_int / (2 ** t)) * np.pi * 2
print("Theta = %.5f" % theta)
# Calculate No. of Solutions
N = 2 ** n
M = N * (np.sin(theta / 2) ** 2)
print("Number of Marked Indices = %.2f" % (N - M))
# Calculate Upper Error Bound
m = t - 1 # Will be less than this (out of scope)
err = (np.sqrt(2 * M * N) + N / (2 ** (m - 1))) * (2 ** (-m))
print("Error < %.3f" % err)
return N - M
回路の実行
全体の回路の実行において、パラメタは次のように置きました。
list0 = [1,3,5,7]
list1 = [8,6,4,2]
C = 22 # 閾値
index_qubits = len(list0) # QRAMのインデックスの量子ビット数
max_l = sum([max(l0, l1) for l0, l1 in zip(list0, list1)]) # QRAMのデータがとりうる最大の値
data_qubits: int = np.ceil(mnp.log2(max_l)) + 1 # QRAMのデータの量子ビット数
C_complement: int = 2 ** (data_qubits - 1) - 1 - C # Oracleで足される定数
qft_qubits = 6 # 位相推定のQFTで使用する量子ビット数(推定精度を決定)
全体の実装についてお見せすると、以下のようになります。
qr_qft = QuantumRegister(qft_qubits, "qft")
qr_index = QuantumRegister(index_qubits, "index")
qr_data = QuantumRegister(data_qubits, "data")
qr_anc = QuantumRegister(1, "ancillary")
cr_qft = ClassicalRegister(qft_qubits, "c_qft")
qc = QuantumCircuit(qr_qft, qr_index, qr_data, qr_anc, cr_qft)
qc.append(quantum_counting(qft_qubits, index_qubits, data_qubits, list0, list1, C_complement), qr_qft[:] + qr_index[:] + qr_data[:] + qr_anc[:])
qc.measure(qr_qft, cr_qft)
(下図は上のコードの出力ではないです。)
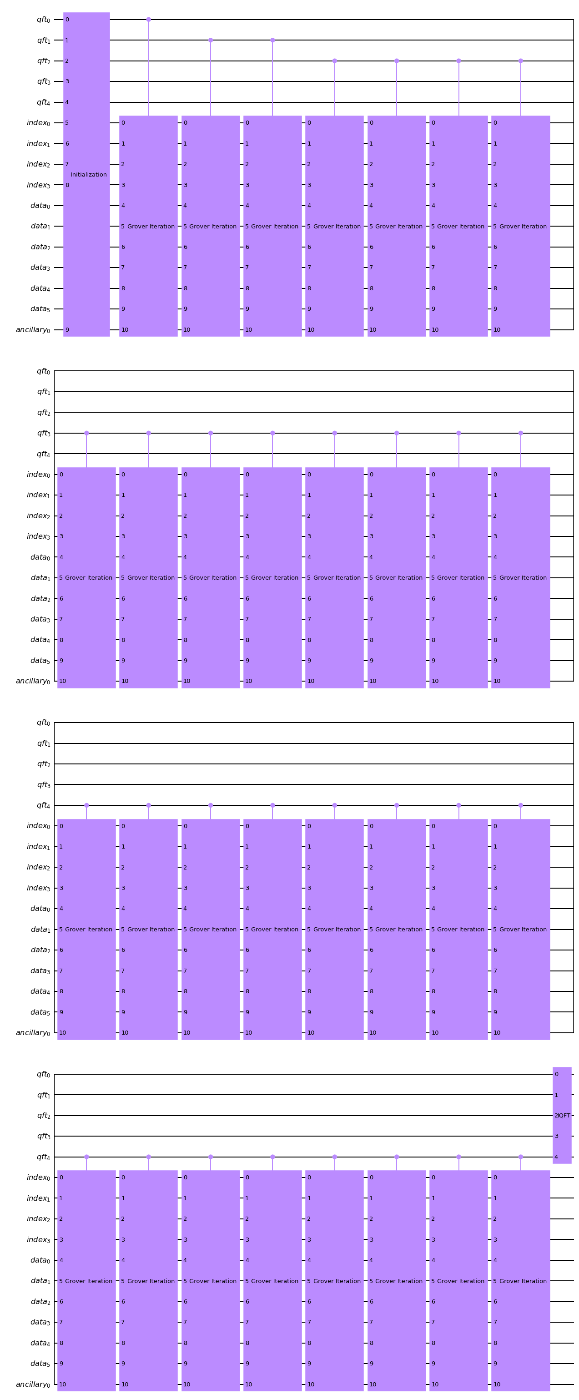
こちらを実行してみると、次のような結果になります。
t1 = time.time()
transpiled_qc = transpile(qc, simulator)
t2 = time.time()
print(t2 - t1, "s")
t1 = time.time()
qobj = assemble(transpiled_qc)
t2 = time.time()
print(t2 - t1, "s")
t1 = time.time()
hist = simulator.run(qobj).result().get_counts()
t2 = time.time()
print(t2 - t1, "s")
plot_histogram(hist)
77.32940173149109 s
1.2563889026641846 s
4.316287994384766 s
(投稿するとなぜかラベルが全部黒塗りになってしまう...)
やはり重いのはtranspileなんですねぇ。
ちなみにtranspile後の回路の深さや基本ゲートの数はだいぶ多いです。
transpiled_qc.num_qubits, transpiled_qc.depth(), transpiled_qc.count_ops()
(17,
99572,
OrderedDict([('mcphase', 48510),
('ccx', 32319),
('cx', 8442),
('u', 7246),
('u1', 3717),
('p', 3529),
('cp', 708),
('u3', 188),
('h', 16),
('measure', 6),
('swap', 3),
('u2', 1)]))
以上の確率分布histから、最終的にC=22より大きい選び方の数は、次のように推定されます。
measured_int = int(max(hist, key=hist.get), 2)
num_markers = calculate_markers(measured_int, qft_qubits, index_qubits)
print(measured_int, num_markers)
Theta = 4.02517
Number of Marked Indices = 2.92
Error < 0.670
41 2.9248537266908325
このように、推定値はおおよそ3だと出力されました。
最後に: 感想や間違いの指摘、改善点の指摘などをいただけると泣いて喜びます!




Discussion
これ、qram_encoderの部分が逆ですね(それに釣られて色々な部分が逆になる)
正しくは、val1とval2を入れ替えて、
なぜなら、最初の設定では、val1が0のデータ、val2が1のデータを表すと決めたから。