🏆

IBM Quantum Open Science Prize 2021参加記録

2022/08/11に公開

量子コンピュータ

量子計算

qiskit

tech

この記事について

今回はIBM Quantum Open Science Prize 2021という、IBMが主催する賞金付きの量子計算マラソンにNaoki Negishiさんとのタッグで参加してきたので、その概要と感想をみなさんに共有しようと思います。

IBM Quantum Open Science Prizeとは

このOpen Science Prizeは、IBMが主催する量子計算に関する賞金付きのコンテストで、今年の開催期間は2021.11.29 ~ 2022.04.16の5ヶ月間で、去年に引き続き今年が2回目の開催です。
競プロのように正解が想定されているわけではなく、形式としてはKaggleや競プロのマラソンに近いような気がします。

出題内容は、基本的には量子計算や、量子計算を使用する各分野への応用に関する重要なテーマが選ばれ、それらについてIBM Quantum Experienceから利用できる超伝導型量子デバイスの上でなるべく良いスコアを出すことを求められます。
賞金は与えられたテーマに対してスコアが最も高かったチーム(1チームとは限らない)に贈られ、賞金額は(今の所)毎年合計100,000USD用意されています。
(高い賞金額に反して僕の周りではこのコンテストがあんまり知られていなくてちょっと意外でした。)

以下、一次情報の関連リンクを置いておきます。

問題

今年の問題は、3粒子XXX Heisenberg spin modelの時間発展をTrotter分解を使用して量子デバイス状でシミュレーションしよう、と言うものです。

より正確には、

H_{\mathrm{Heis}}=\sum_{\langle i j\rangle}^{N} J\left(\sigma_{x}^{(i)} \sigma_{x}^{(j)}+\sigma_{y}^{(i)} \sigma_{y}^{(j)}+\sigma_{z}^{(i)} \sigma_{z}^{(j)}\right)

の

N=3

の場合である、

H_{\text {Heis3 }}=\sigma_{x}^{(0)} \sigma_{x}^{(1)}+\sigma_{x}^{(1)} \sigma_{x}^{(2)}+\sigma_{y}^{(0)} \sigma_{y}^{(1)}+\sigma_{y}^{(1)} \sigma_{y}^{(2)}+\sigma_{z}^{(0)} \sigma_{z}^{(1)}+\sigma_{z}^{(1)} \sigma_{z}^{(2)}

が与えられたとします。
このHamiltoniaをSchrödinger方程式

i \hbar \frac{d}{d t}|\psi(t)\rangle=H|\psi(t)\rangle

に従って時間発展させた時の時間発展演算子

\begin{array}{lll} U_{\text {Heis3}}(t)&=&e^{-i t H_{\text {Heis } 3}}=\exp \left(-i t H_{\mathrm{Heis} 3}\right) \\ &=&\exp \left[-i t \sum_{\langle i j\rangle}^{N=3}\left(\sigma_{x}^{(i)} \sigma_{x}^{(j)}+\sigma_{y}^{(i)} \sigma_{y}^{(j)}+\sigma_{z}^{(i)} \sigma_{z}^{(j)}\right)\right] \\ &=&\exp \left[-i t\left(\sigma_{x}^{(0)} \sigma_{x}^{(1)}+\sigma_{x}^{(1)} \sigma_{x}^{(2)}+\sigma_{y}^{(0)} \sigma_{y}^{(1)}+\sigma_{y}^{(1)} \sigma_{y}^{(2)}+\sigma_{z}^{(0)} \sigma_{z}^{(1)}+\sigma_{z}^{(1)} \sigma_{z}^{(2)}\right)\right] \end{array}

をTrotter分解することで、量子回路に落とし込んでシミュレーションしようということです。
(Trotter分解の仕方は自由に変更して良い)

制約は、

4 trotter step以上用いること
Fidelityが $0.3$ を超えること

の2点です。

提案手法

上記の問題設定において、通常のTrotter分解をすると、1 trotter stepあたりCNOTゲート数が6個必要になり、ノイズなしのシミュレーションでもfidelity $0.8$ を達成するためには8 trotterは必要なので、そうすると50個近くCNOTゲートを消費することになります。

これは実機上ではかなり無理な設定なので、なんとかCNOTの数と、回路の深さを減らさなければいけません。

僕らのチームは与えられたHeisenberg Hamiltonianの対称性に注目し、Effective Hamiltonianを構成することで、回路の深さと登場するCNOTの数の削減を行いました。
これは、Trotter軸の変更に対応しており、3-qubitに作用していたHeisenberg Hamiltonianを、2-qubitのみに作用するEffective Hamiltonianにエンコード(座標変換)し、そのEffective HamiltonianをTrotter分解する、という戦略です。
そして最後にまた座標変換で3-qubitに戻せばいいわけです。
以下簡単に手法の概要を説明しますが、詳しくはGitHubに置いた僕らの提出物にあるreport.pdfを見てください。

全ては与えられたHeisenberg Hamiltonianの対称性である、

\left[H_{\mathrm{Heis}}, \sigma_{\mu}^{1} \sigma_{\mu}^{2} \sigma_{\mu}^{3}\right]=0

から導かれます。
この対称性により、与えられたHeisenberg Hamiltonianは、以下の2つの空間において同様の時間発展をすることがわかります。

\mathcal{H}_{\mathrm{odd}} =\{|001\rangle,|010\rangle,|100\rangle,|111\rangle\}\\ \mathcal{H}_{\mathrm{even}} =\{|110\rangle,|101\rangle,|011\rangle,|000\rangle\}

つまり、元々3-qubitで時間発展させていたのは冗長で、本質的な時間発展に関する情報を2-qubitに押し込めることができます。

この3-qubitから2-qubitへのエンコーディングは以下のユニタリ演算で実現できます。

U_{\mathrm enc}=\left(\begin{array}{cccccccc}1&&&&&&&\\&&&1&&&&\\&&&&&&1&\\&&&&&1&&\\&&&&&&&1\\&&&&1&&&\\&1&&&&&&\\&&1&&&&&\end{array}\right)

この操作は、3-qubitから2-qubitに埋め込む場合はCNOT5個で実現できます(下の方の図を参照)。
これを用いると、3-qubitにおける与えられた冗長なHamiltonianから、次のような2-qubitのEffective Hamiltonianが得られます。

\begin{aligned}H_{\mathrm{eff}} =U_{\mathrm{enc}} H_{\mathrm{Heis} 3} U_{\mathrm{enc}}^{\dagger}=\sigma_{x}^{1}+\sigma_{x}^{2}+\sigma_{z}^{1}+\sigma_{z}^{2}-\left(\sigma_{z}^{1} \sigma_{x}^{2}+\sigma_{x}^{1} \sigma_{z}^{2}\right) \end{aligned}

次に、コンテストのルールで要求されているTrotter分解を使用するために、このEffective Hamiltonianを以下のようにTrotter分解します。

\begin{aligned} \exp \left(-i H_{\mathrm{eff}} t\right) &=\exp \left[-i t\left\{\left(\sigma_{x}^{1}+\sigma_{z}^{2}-\sigma_{x}^{1} \sigma_{z}^{2}\right)+\left(\sigma_{x}^{2}+\sigma_{z}^{1}-\sigma_{x}^{2} \sigma_{z}^{1}\right)\right\}\right] \\ &=\displaystyle\lim _{n \rightarrow \infty}\left[e^{\frac{-i t}{n}\left(\sigma_{x}^{1}+\sigma_{z}^{2}\right)} e^{\frac{i t}{n}\left(\sigma_{x}^{1} \sigma_{z}^{2}+\sigma_{x}^{2} \sigma_{z}^{1}\right)} e^{\frac{-i t}{n}\left(\sigma_{x}^{2}+\sigma_{z}^{1}\right)}\right]^{n}\end{aligned}

この操作は以下の量子回路で表現できます。

trotter_block

このTrotter blockを繰り返すことで、Trotter分解の近似精度を上げていく、というわけです。

エンコーディングとデコーディングを含めた量子回路全体は以下の図になります。(4 Trotter stepの場合)
general_circuit

今回は問題設定で初期状態を $|110\rangle$ から開始する、と言われているので、そのような初期状態に対してさらに最適化を行うと、
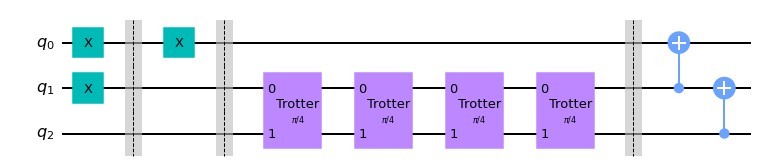
specific_circuit
エンコーディングとデコーディングの部分でCNOTをこのように削ることができます。

さらに、時間発展幅も $0\sim\pi$ と言われているので、時間発展の周期性に着目して、
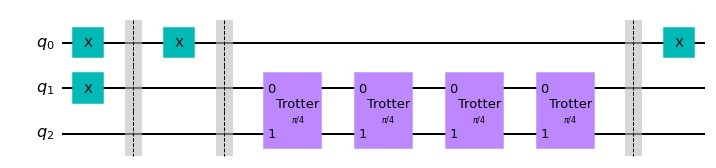
shallow_circuit
のように、CNOTを使わずにエンコーディングとデコーディングができます。
この辺りはルール的にはグレーですが、違反していないことをレポートの中で示しました。

まとめると、僕らの手法は、古典計算でシミュレーションを実質的に計算することなく、 $N=3$ の系において、任意の初期状態と時間発展に対して適用することができ、状況次第では更なる最適化が可能なものとなっています。

ここまでなら、まだCNOT gateは $n$ ステップのTrotter分解に対して $2n$ 個使っているので、実機で良い結果を出すには大変よろしくないのですが、実はKAK decompositionなどの回路最適化手法を駆使することで、2-qubit間の同じ方向を向いたCNOTたちを相殺することが可能です。
この手法はqiskit.compiler.transpile関数のoptimizaiton_level=3オプションで実装されていて、実際に、先ほどの回路:
specific_circuit
は、以下の回路のように最適化されます。
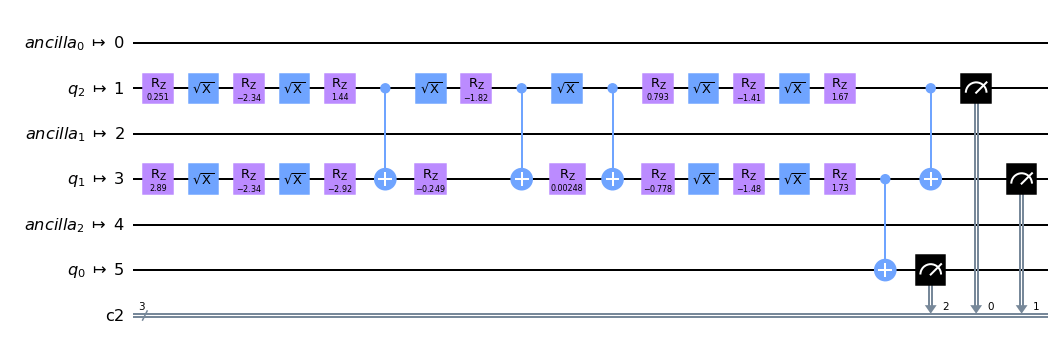
optimized_cirucit

これがかなり強力で、分解するTrotter stepに関わらず、Effective HamiltonianのTrotterizationは最終的に定数段(定数個)のCNOTで済むということになります。

というわけで、あとはQuantum Error Mitigation (QEM, 量子誤り軽減)をいくつか取り込んであげれば、実機上で非常に高いFidelityが見込めそうですね!
今回はQEMとして、

zero-noise extrapolation (ZNE)
quantum readout error mitigation (QREM)

を使用し、プロセスの全体図としては、次のようになります。
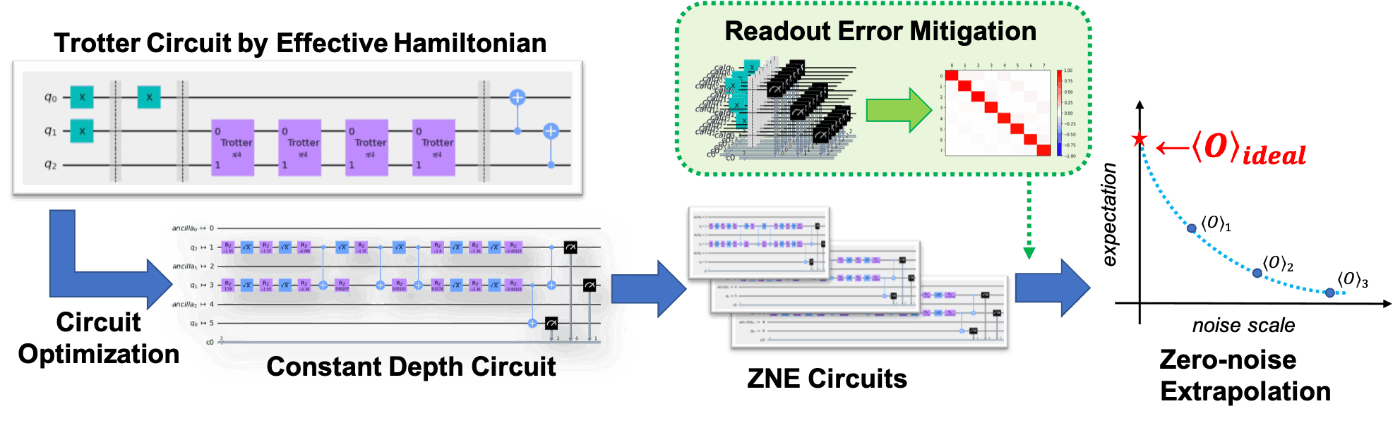
workflow

ZNEの使用に関しても賛否諸説ありますが、運営側はOKだと認めたので、ぜひ使っていこうと思います。
というのも、デバイスベンチマーキングにおいてはZNEを使うのはある意味邪道で、実際のデバイスの様子が知りたいのに、ノイズフリーな期待値を外挿で求めるというのは、何も実機の状態を反映しないことになるからです。
一方で、量子情報処理において、実機から意味のある結果を取り出す、という観点ではZNEは強力な手法になり得ます。

以上を用いて、僕らの手法では最終的にはFidelity $0.9929\pm 0.0015$ を叩き出しました。

コンテストの結果

優勝者は2022年8月10日に告知され、Oxfordの学生グループがIncremental Structural Learning (ISL)という手法を用いて総合1位を取ったようです。
(早くこの記事を投稿したいので彼らの手法の詳細はここでは述べませんが、1位にふさわしい提出物でした。)

優勝者の評価方法は

score of fidelity (相対評価): 15点
clarity of document: 5点
originality / generality: 5点

の25点満点(整数)での勝負です。

僕らの手法はFidelityが0.99を超えているので、素点で1位を取れると思っていたのですが、僕らとほぼ同じアイデアのチームがより高いFidelityを出していましたし、上で説明した手法では一般性(n-qubitへの拡張)に欠ける + 2-qubitならTrotter分解を使うメリットがない、といった問題点は確かにあります。
どのチームが何点取ったかは公表されませんが、僕らの手法はきっと芸術点(originality / generality)で劣っていたのでしょう。

いずれにせよ、優勝チームに最大限の賞賛を送りたいと思います!

コンテストのアクセシビリティ

コンテストの主催者からの告知や、主催者への質問のやりとりは主にQiskit slackの鍵チャンネルで行われていて、去年11月末のコンテスト開催告知の時に一斉に招待されるようです。
僕ら3月からこのコンテストに取り掛かったので、slackチャンネルの存在は4月に主催者に質問を投げるまで知らないままでした(slackの存在を公に告知していないのはどうして...)。

また、コンテストでは提出に関するルールがかなり明確に記されているのに、締切日直前になって突然締切が1週間延長になったという告知がなされたので、割と場が荒れていました。

採点方法については、運営側の一存で、上で書いた通り他のチームの点数などは公開されません。
他のチームの手法については元々bemyappというプラットフォームでオープンにするつもりだったようですが、上で述べた締切延長のゴタゴタで無くなってしまいました。

賞金については去年は4チームで山分けだったので今年もそうかなと思ったら、今年は1チームしか選ばれなかったようで、ちょっと悲しいです。
Kaggleや競プロみたいに2位以下にも何らかの賞があったりするとよかったです。
この点に関しては、参加者全員が納得するような全順序での順位づけができるかどうかはかなり怪しいので、今の状態のルールになっているのも納得はできます。

参加した感想

今回はNaoki Negishiさんとチームを組んでの参加で、役割分担としては、Naokiが主に手法を提案し、僕がプログラムの実装と誤り軽減の応用を主に担当しました。
彼の的を射た考察と画期的なアイデアにはいつも驚かされるばかりでしたし、僕もこれまで培ってきたQiskitのエンジニアリングの経験と論文執筆の経験を活かすことで、チームで非常に良い役割分担ができたかなと思っています。

このコンテストに本格的に取りかかれたのは4月に入ってからで、締め切りに間に合うかどうか怪しかったですが、結果的に提出にこぎつけられたのでよかったです。
というのも、他のチームも締め切りギリギリにjobを実機に提出していたので、実機の待ち時間(queue)が非常に長くなって、僕らが提出した頃には、jobを投げてから結果が返ってくるまでに5日も待たなければいけない状況でちょっとヒヤヒヤしたりしました。

また、今回せっかくここまで議論を進めることができたので、まだまだ詰める部分はありますが、ここまでの結果をある程度拡張して、可能ならば論文化できるよう取り組んで行きたいと思います。

最後に、企画運営してくださったIBMのスタッフの方々に深く感謝を申し上げたいと思います。
また、ここまで読んでくださった読者の方々も大変ありがとうございます。
昨今では様々な賞金付き量子ハッカソンが開かれているようですし、みなさんもぜひ来年のOpen Science Prizeに参加してみてはいかがでしょうか？