Zenn
📝

中心差分を用いた接線の交点の求め方とPythonのライブラリであるmatplotlibによる可視化

2023/07/30に公開
1件
Python
Matplotlib
交点
中心差分
接線
idea

この記事は、Qiitaにも投稿してます!!
詳しくは下のリンクから↓
https://qiita.com/blueman/items/542064585cd44f894494

はじめに

様々な関数の任意の2点の接線の交点を求めると面白そうだったので、2つの接線の交点のx座標とy座標の式を求めました。
また、Pythonのライブラリである matplotlib を用いて関数のグラフ、任意の2点を通る2つの接線、2つの接線の交点を描画しました。

よろしければこちらもどうぞ!!

マイページについて

マイページはこちら

X(Twitter)について

X(Twitter)はこちら

Qiitaについて

実行環境

実行環境は次の通りです。

実行環境
  • 環境
    • Windows 10
    • Python 3.10.5
  • ライブラリ
    • matplotlib 3.6.1

接線の交点の座標の求め方

微分係数を用いた接線の公式は、任意のx座標をaとし任意の関数をf(x)とすると x座標のときのy座標 はf(a)と表せます。
また任意のx座標での微分係数をf'(x)とし、これを用いると任意の点での接線の傾きを求められ x=aでの傾き はf'(a)と表せます。
これらの値から x=aでの接線 は、以下のように表せます。

\begin{gather} y-f(a)=f'(a)(x-a) \end{gather}

ここで、新たに任意のx座標をbとし上記と同様に考えると、接線は以下のように表せます。

\begin{gather} y-f(b)=f'(b)(x-b) \end{gather}

(1)-(2)より、

\begin{aligned} f(b)-f(a) & =\Bigl(f'(a)-f'(b)\Bigl)x+f'(b)b-f'(a)a\\ \Bigl(f'(a)-f'(b)\Bigl)x &= f(b)-f(a)-f'(b)b+f'(a)a\\ \end{aligned}

よって、

\begin{gather} x=\frac{f(b)-f(a)-f'(b)b+f'(a)a}{f'(a)-f'(b)} \end{gather}

また、(1)\times f'(b)より、

\begin{gather} f'(b)\times y-f(a)\times f'(b)=f'(a)\times f'(b)\times x-f'(a)\times f'(b)\times a \end{gather}

一方で、(2)\times f'(a)より、

\begin{gather} f'(a)\times y-f'(a)\times f(b)=f'(a)\times f'(b)\times x-f'(a)\times f'(b)\times b \end{gather}

(4)-(5)より、

\begin{aligned} \Bigl(f'(b)-f'(a)\Bigl)y+f'(a)f(b)-f(a)f'(b) & =f'(a)f'(b)b-f'(a)f'(b)a\\ \Bigl(f'(b)-f'(a)\Bigl)y&= (b-a)f'(a)f'(b)-f'(a)f(b)+f(a)f'(b)\\ \end{aligned}

よって、

\begin{gather} y= \frac{(b-a)f'(a)f'(b)-f'(a)f(b)+f(a)f'(b)}{f'(b)-f'(a)} \end{gather}

したがって、(3)と(6)が2つの接線の交点のx座標とy座標です。

微分係数の求め方

ここで、微分係数の定義式を考えると、

f'(a)=\lim_{h \to 0}\frac{f(a+h)-f(a)}{h}

であり、hを0に近づけるという極限操作をしなければなりません。しかし、コンピュータ上では極限操作を行うことができません。

そこで、数値微分を行うことで近似的に微分係数を計算しました。
数値微分における3つの差分とその誤差についてを参照すると、

中心差分が最も接線の傾きに近い

らしいので中心差分を用いて微分係数を求めることにしました。ちなみに、中心差分は以下の式で求められるそうです。

f'(x)\approx \frac{f(x+h)-f(x-h)}{2h}

ソースコード

実行環境で示した環境で実行すればおそらく動くはず。

ソースコード
sessen_kouten.py
#任意の関数の二接線の交点の座標を算出

#ライブラリのインポート
import numpy as np
import matplotlib.pyplot as plt

#中心差分の式のhを定義
h = 10**(-4)

#aとbを定義
a = -2
b = 2

x = np.linspace(-10,10,1001) #xの値を定義

'''接線の交点を求めたい関数の宣言
本コードでは

 y=x^2

とした'''

def func(x):
	return x**2

#定義したa,bでの微分係数の計算
dydx_a = (func(a+h)-func(a-h))/(2*h) #x=aでの微分係数
dydx_b = (func(b+h)-func(b-h))/(2*h) #x=bでの微分係数

y_a = dydx_a*x-dydx_a*a+func(a) #x=aでの接線の計算
y_b = dydx_b*x-dydx_b*b+func(b) #x=bでの接線の計算

'''交点のx座標を計算

          f(b)-f(a)-f'(b)b+f'(a)a
x_交点 =  ----------------------
               f'(a)-f'(b)

'''

x_inter = (func(b)-func(a)-dydx_b*b+dydx_a*a)/(dydx_a-dydx_b)

'''交点のy座標を計算

          (a-b)f'(a)f'(b)+f'(a)f(b)-f'(b)f(a)
y_交点 =  -----------------------------------
                     f'(a)-f'(b)

'''

y_inter = ((a-b)*dydx_a*dydx_b+dydx_a*func(b)-dydx_b*func(a))/(dydx_a-dydx_b)

#print("f(a) = {:.3f}".format(func(a))) #コメントアウトを外すとx=aでのy座標が出力される
#print("f'(a) = {:.3f}".format(dydx_a)) #コメントアウトを外すとx=aでの微分係数が出力される
#print("f(b) = {:.3f}".format(func(b))) #コメントアウトを外すとx=bでのy座標が出力される
#print("f'(b) = {:.3f}".format(dydx_b)) #コメントアウトを外すとx=bでの微分係数が出力される
#print("x_inter = {:.3f}".format(x_inter)) #コメントアウトを外すと2つの接線の交点のx座標が出力される
#print("y_inter = {:.3f}".format(y_inter)) #コメントアウトを外すと2つの接線の交点のy座標が出力される

#print("(%f,%f)" % (x_inter,y_inter)) #コメントアウトを外すと2つの接線の交点の座標が出力される

plt.xlim(-10,10)  #x軸の表示範囲を制限
#plt.ylim(0,2) #y軸の表示範囲を制限
plt.plot(x,func(x)) #任意の関数のグラフを描画
plt.plot(x,y_a) #任意の関数のx=aでの接線を描画
plt.plot(x,y_b) #任意の関数のx=bでの接線を描画
plt.scatter(x_inter,y_inter) #2つの接線の交点を描画

#plt.plot(x,np.zeros(len(x))) #コメントアウトを外すとx=0の直線を描画
plt.show()

結果

ソースコードを実行した結果は次の通りです。

実行結果のグラフ


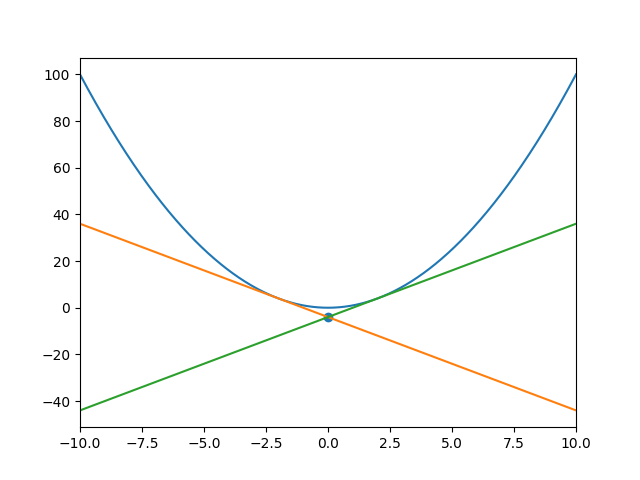
グラフ

実行結果のコマンドプロンプト上の表示


計算結果

まとめ

関数の任意の2点の接線の交点のx座標とy座標を求め、その結果をもとに Python のライブラリである matplotlib を用いて接線の交点を描画しました。
この記事が実際に役に立つかどうかは分からないですが、誰かの役に立ってくれると嬉しいです。
記事を執筆する余力があれば、次回も記事を投稿する予定です。
次回の予定としては、中心差分を用いて画像の画素ごとの微分を行ってその結果をPythonのライブラリであるOpenCVを用いて表示させたのでそれに関する記事を投稿する予定です。

Discussion