Static Top Treeの覚書
はじめに
AtCoder Beginner Contest 351のG問題の解説にStatic Top Treeというものが出てきました。この記事は、公式解説と解説放送を見た上で、Static Top Treeがどんなものなのかを、自分なりの解釈で、未来の自分用にまとめたものです。間違っていることが書いてあれば、やさしく教えてくださると助かります。
公式解説と解説放送によると、Static Top Treeというのは、競技プログラミング界隈の俗な名称だそうです。オリジナルのTop Treeはこちらの論文で紹介されたそうで、今回のStatic Top Treeとは異なるようです。
この記事を理解するにはHeavy-Light分解(HL分解)の基本的な知識が必要になります。
どんなデータ構造か
Static Top Treeは木の生成過程を二分木として表現して持つデータ構造です。
元の木と、生成過程を管理する木の二つがあるので、元の木の頂点を(木の)頂点、辺を枝と呼ぶことにし、生成過程を管理する木の頂点をノード、辺を辺と分けて呼ぶことにします。
具体的には、次の操作を繰り返し行なって目的の木を生成します。
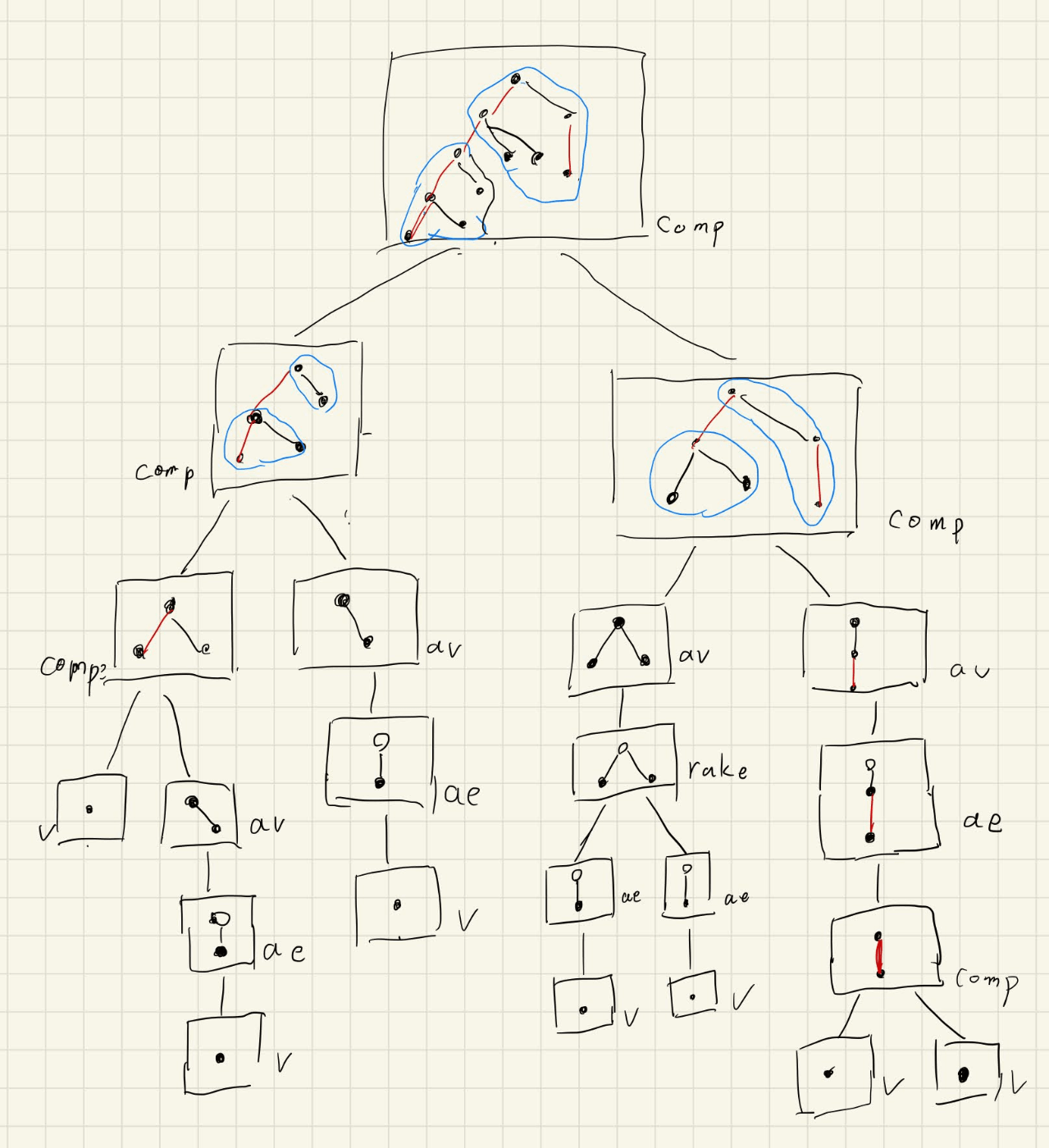
(1) 二つの部分木にHeavy Edgeを追加し、1つの部分木にする(Compress)
(2) 部分木の根のvirtualな頂点を、通常の頂点に置き換える(Add Vertex)
(3) virtualな頂点を根とする二つの部分木を、virtualな頂点を合体させることで一つの部分木にする(Rake[1])
(4) 実際の頂点を根とする部分木に、Light Edgeとvirtualな頂点を追加し、そのvirtualな頂点を根とする部分木にする (Add Edge)
(5) 何もない状態から、実際の頂点を追加する (Vertex)

Static Top Treeを構築する際には、これらとは逆の操作を適用して木を分解していきます。分解していくことで、逆順に構築過程を構成できます。
なお、CompressとRakeにおいては、左右に振り分ける部分木の大きさがおよそ半分になるようにします。このようにすることで、二分木が平衡するようにします。
例えば、次のような木の生成過程が考えられます。図ではHeavy Edgeを赤線、Light Edgeを黒線、virtualな頂点を白丸、実際の頂点を黒丸で表現しています。
実装
前節の操作の図と例を観察すると、どの操作の前にどの操作を実行すればいいかがわかります。
- Compressの前は、CompressまたはAdd Vertex、Vertexが実行される
- Add Vertexの前は、RakeまたはAdd Edgeが実行される
- Rakeの前は、RakeまたはAdd Edgeが実行される
- Add Edgeの前は、CompressまたはVertexが実行される
- Vertexの前は何も実行されない
公式解説と解説放送では、CompressはHeavy Path全体に、Rakeは一つの部分木のすべての子に対して一気に実行されるようになっています。どちらの実装でも、mergeをいう便利関数を用意し、それを使ってHeavy Path/Light Edgeの先の子を平衡になるように分割しています。本実装でもそのようにしました。おそらく、部分木の大きさを評価する回数が一回で済むようにそのようになっているのだと思います。
実装はGitHubの僕のライブラリーのリポジトリにあります。
何が嬉しいか
平衡でなく、二分木でない木を、頂点数の大きく変わらない平衡な二分木で管理できることにあるんだろうと思います。
平衡でない木を平衡な木で管理できる
パスグラフに対してStatic Top Treeを構築すると次のようになります。パスをうまく分割することで、平衡な木にできていることがわかります。

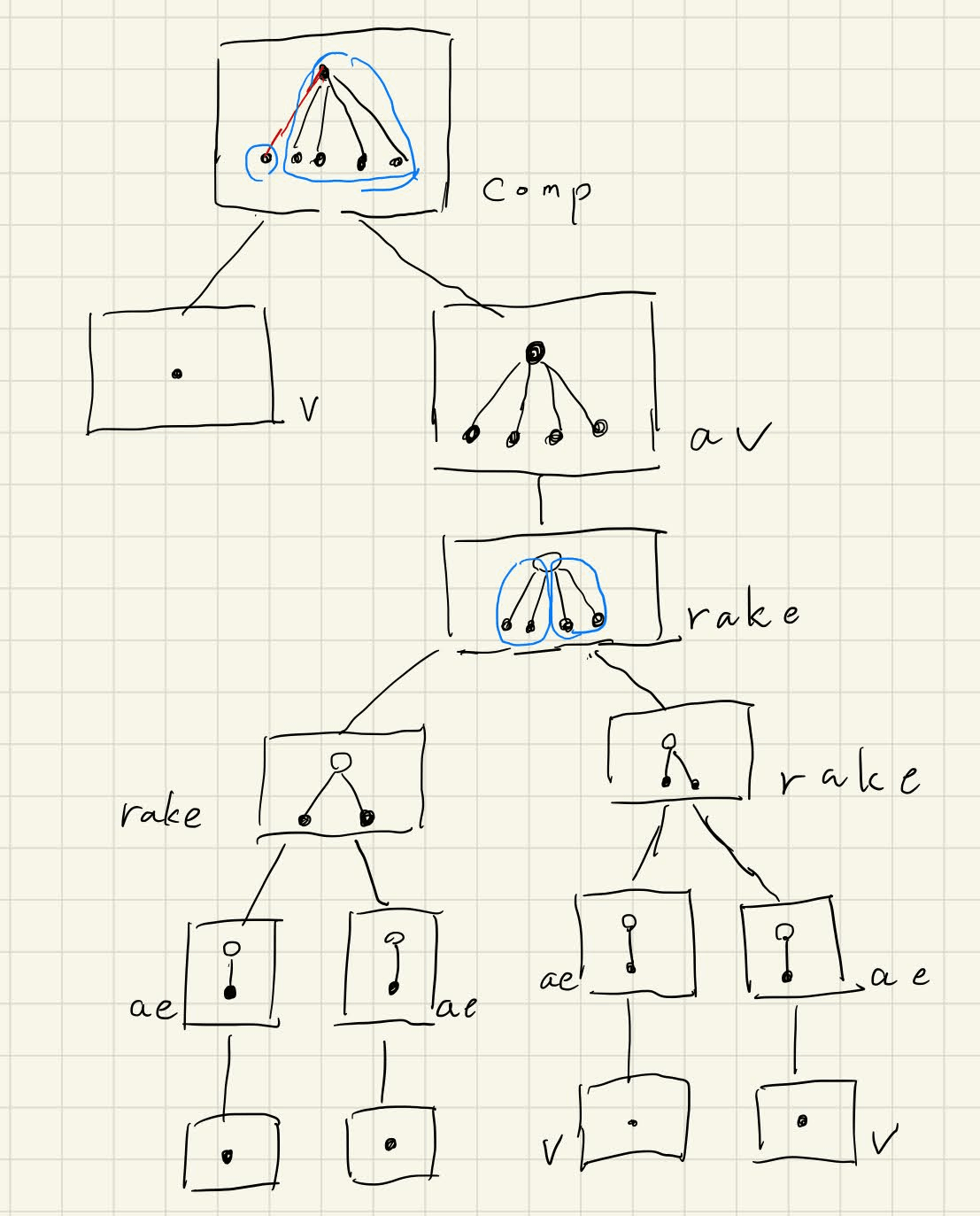
二分木でない木を平衡な二分木で管理できる
スターグラフに対してStatic Top Treeを構築すると次のようになります。Heavy Edgeの先の頂点以外は平衡しています。二分木で管理できているので、兄弟がいっぱいいいるような頂点への更新であっても、log程度のノードを辿れば更新が終わります。
ノード数が大きく変わらない
Static Top Treeのノード数は
- Compress: Heavy Edgeの本数だけ(Heavy Edgeを増やすので)
- Add Vertex: 葉でない頂点の数だけ(葉でない頂点を作るので)
- Rake: Light Edgeの本数だけ
- Add Edge: Light Edgeの本数だけ(Light Edgeを増やすので)
- Vertex: 葉である頂点の数だけ(葉を作るので)
であることがわかります。Add VertexとVertexの回数を足すと
Static Top Treeはできるだけ平衡するように作ったので、高さは
よくわかっていないこと
どんな代数構造を載せられるか
セグメント木がモノイド(単位元と結合律あり)のみを扱えるように、Static Top Treeで扱える演算にも制限があるはずですが、条件がよくわかっていません。
実際の頂点を根とする部分木をPath Cluster、virtualな頂点を根とする部分木をPoint Clusterと呼ぶらしく、解説実装でも本実装でも、それぞれに対応するデータ構造をPath、Pointと呼んでいます。
現在、理解していることとして、
- Path同士の演算は結合律を満たす必要がある。(Compressの順番を操作するために必要)
- Point同士の演算は結合律を満たす必要がある。(Rakeの順番を操作するために必要)
- (解説実装、本実装では)Point同士の演算は可換律を満たす必要がある。(HL分解とグラフの根付き木化の実装の都合上、枝の順番を入れ替えている)
があります。
他の応用
ゴールデンウィークでまだ時間はありますが、僕のレートだとレートを上げるためにStatic Top Tree以外にやることがあるので、公式解説で紹介されていた練習問題や類題には手を出していません。
参考文献
-
熊手などでならすという意味らしい https://ejje.weblio.jp/content/rake ↩︎
Discussion