Zenn
Open15

幾何中央値で求める日本の中心

Common Lisp
幾何中央値
biofermin2biofermin2

以前国土交通省の位置参照情報の緯度経度データを元に
ある住所を表示するための地図ライブラリを作成したけど、
作成したものの求める緯度経度が中央には表示出来ない
といった不満があったり、そのためにはjavascriptも勉強
しないといけないよなぁと思いつつ、いろいろあって
放置してるプログラムがある。
https://github.com/biofermin2/jpmap

途中であってもそこまで出来た部分もあるので、
それはそれでネタになるかなと思ってはいた。
ただ頭の中にあるものを一気に書く事を考えると、
筆がなかなか進まないので、復習やリファクタリングも兼ねて
少しずつ書き進めたいと思う。

biofermin2biofermin2

世界の中心で愛を叫ぶというドラマか映画が以前話題になってたけど（個人的にはまだ見た事はない）、
じゃあ日本の中心で愛を叫びたい人にとってどこで叫んだらいいのか？
実際この文章を書いている現段階では自分もそれがどこか知らない笑

別に個人的に愛を叫びたい！って訳ではないけど、
元はと言えば気象関係のプログラムを作成してて、
市町村などの地理的な中心ってどこになるんだろう？
そういう疑問を持ち始めたのが事のきっかけ。

当初は何も疑問も持たず、ある行政区の東西南北限を四辺とする四角形の
それぞれの辺を２で割った位置を繋げて出来る線の交差する点を
中心点だろうと当たり前のように思い、当たり前のようにそれを計算して使っていた。

（上の緑の箇所はとある行政区内を表現している。）

しかし、実際やってみるとブーメランみたいな丁度真ん中が海となったり、
あるいは隣の行政区になったりする地形の行政区もあったりする。

例えば東京都だと、小笠原諸島も東京都だから東京都の中心は東京湾から南海上のどこかとなる。

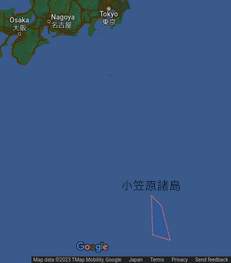
しかし、そんなところを都心なんて言ってたらいつも都心の様子は
海の様子を映すだけで、実際の都合上全く用を成さない。

数学の世界ではある集団の特徴を１つの数値で表したものを代表値というらしいが、
その代表値を求める方法としてだいたい次の方法が挙げられる。
平均値
中央値
最瀕値
このあたりの数学的な細かい違いについてはネット上で既に
たくさん説明しているサイトがあるのでここでは割愛。

自分はこの中でも平均値を出すような手法で当初求めてた
訳だが、上記のような問題が実際発生してしまう。

海や隣の行政区ではなく確実にその行政区内のどこかの地点を求めるには
中央値的な手法が有効になってくる訳だが、
それの地形上の中央値を求める方法として
幾何中央値という概念がある事を知った。

日本語のwikipediaはまだ現時点では存在していないけど、
英語版はこちら。
幾何中央値とかgeometric medianでググってもまだ気のせいか
まともに記述している日本語のサイトがここ以外見当たらない。
そういう意味では貴重な文章になるとは思う。

ちなみに幾何中央値の定義は以下の通り。

{\displaystyle {\underset {y\in \mathbb {R} ^{n}}{\operatorname {arg\,min} }}\sum _{i=1}^{m}\left\|x_{i}-y\right\|_{2}}

以上。と言いたいところだが笑、自分みたいな人間は数学の記号を見ても
なかなかパッと理解出来ないので、なるべく丁寧に記号の意味を見ていこう。

詳しい解説はここをクリック

数学ではいろんな記号が出てくる。
そういう記号を見るだけで拒絶反応を示してしまうかもだけど、
元々非常に多くの言葉で説明を要する話を簡単に現すために用いたのが記号。
信じがたいかも知れないが、本来は便利な道具なのだ。
全部覚えるとなると大変だろうけど、org-modeと一緒で
必要に応じてその都度意味を調べ使えるようになればいいだけだと思う。

まず頭の\argminだが、最小点集合と呼ばれるもので、
これはあくまで最小値ではなく次に来る関数が最小値となる値の集合を意味する。

y\in\R^nという部分は
yと名付けたものが実数の集合\R^nに含まれる事を意味する。
つまりyも何かしらの実数を示す。

\R^nのnだが、直積集合というものを表していて、
わかりやすく言うと次元数にあたるらしい。
つまり\R^2だと平面上の実数点全てを表し、
\R^3だと空間上の実数点全てを現すという具合。
それがn次元あるという意味。

次に右側の関数部分についてだが、

\sum _{i=1}^{m}\left\|x_{i}-y\right\|_{2}

は数列の和を意味している。
何の数列の和かというとある点yと各点x_iとのユークリッド距離の和。
ユークリッド距離というのはわかりやすく説明すると三平方の定理で求められる２点間の距離。
つまり点yと点x_iとの距離をdistanceのdを使って{\displaystyle d_{i}(x_{i},y)}で現すと

{\displaystyle d_{i}(x_{i},y)={\sqrt {(x_{i1}-y_{1})^{2}+(x_{i2}-y_{2})^{2}}} =\left\|x_{i}-y\right\|_{2}}

\sumの下はxの添字iの始まりの数を表していて、それが1から始まりますよという意味。
\sumの上の字は添字iの終わりの数を表していて、最大mまであるという事を指している。
つまり上の三平方の定理をx_1\dots x_mまで適用してyからの距離をそれぞれ求めた
ものd_1\dots d_mの和を求めていくという話。

\left\|x_{i}-y\right\|_{2}についてよく|a|は絶対値だが、||a||も時折
絶対値と記述されているところもある。ただ、||a||の場合は通常ノルムといって
ベクトルの大きさを表記する時に使う。ベクトルはいずれの向きも大きさが負に
なる事が無いので、絶対値と似たようなものだけど、厳密には
そういう意味の違いがあるらしい。そして最後の２という数字だが
これはノルムの次元を表している。よってこれは2次平均ノルムだとか簡単に2-ノルム
と言われたりしている。また２次元の時のみユークリッドノルムとも言われる。
この次元数が言わば累乗根の数と一致してくる。\sqrt[2]{x}というのは別名平方根と
言われ、通常は2は省略されて\sqrt{x}と表記される。
\sqrt[3]{x}は立方根、\sqrt[p]{x}は累乗根と言われる。
ここで出てくるpがノルムの次元と一致するので、その場合p次平均ノルムだとかp-ノルム
と呼ばれる。ここでは２なのでノルムを求める三平方の定理の式が平方根となっている。

ここらへんの話は深入りすると本題からそれるので、そういう意味なのかという
程度で理解していただけたらと思う。
より詳しく知りたい場合は個々人でお調べ下さい笑

話をまとめると実数集合R^n上に存在するx_1\dots x_mとの
距離の和が最小となるようなyの集合の事を幾何中央値と呼ぶ訳だ。

間違ってたらご指摘下さい。

では実際、地図上における各点とは何か？
今回調べるに当たって活用したデータは
国土交通省の位置参照情報ダウンロードサービスのデータを使わせて頂いた。
このデータで使われている各大字町丁目名毎にある緯度・経度をその各点とした。

ちなみにその各点である緯度・経度をどうやって算出しているのか
国土交通省の国土情報提供サイト運営事務局
に直接問い合わせてみたところ、以下のようなご回答を頂いた。

これは任意の代表点の緯度・経度となっています。
必ずしも地理的な中心点というわけではなく、
自治体によって代表的な位置の取り方や基準が異なる可能性がございます。
また、同じ大字町丁目であっても、年度によって代表地点の位置が異なっている場合もあるようです。

という事で、基準となる点もあくまで参考となるデータであり、
従って自分がこれから求めていく中心もあくまで参考と考えて
軽い気持ちで見ていただけたらと思う。

biofermin2biofermin2

では自分も忘れてる部分もあるので、実際に手を動かしながら説明する。
上記の国土交通省の位置参照情報ダウンロードサービスのリンク先を
クリックして開く。
その中に都道府県単位というボタンがあるので、それをクリック。
調べたい都道府県をチェックを入れたら街区ではなく、
全ての大字・町丁目レベルにチェックをして選択、同意して
ダウンロード。

令和３年度のデータだと15.0bという版数のデータがダウンロードされる。
街区レベルの20.0aという版数のデータだと用途としては細かすぎるので、
そちらは使用しない。

データはzip形式でダウンロードされるが、解凍すると中に１つ
csvファイルがある。文字コードはshift_jisを使っている。
csvファイルの中身は下図の通り。

biofermin2biofermin2

この中で使う列はB，D，F，G，H。
csvから特定の列だけを抽出する時はawkだとか
cutだとかがパッと思いつく訳だが、
今まで通りそれを使ったのでは面白くない笑

common lispからコマンドラインを実行する方法もあるが、
敢えて易きに流れず、common lispで関数を自作する。

(defun cut (file &key to key val (title t) (use nil) &aux (k-len (length key)))
  "ファイルから必要な列のデータを抽出し、
ハッシュテーブルにセット。その際タイトル行があれば省く"
  (with-open-file (in file)
    (loop :for line = (read-line in nil nil)
       :while line
       :collect (multiple-value-bind (k v)
		    (divide (loop :for i :in (append key val)
			       :collect (nth i (parse-line line))) k-len)
		  (cond ((and (not title) use)
			 (error "no header.you should delete use keyword from this function."))
			((or (and title use) (and (not title) (not use)))
			 (put-ht k v to))
			((and title (not use))
			 (setq header (list k v)
			       title nil))))))) ; => CUT

細かい周辺の関数はソースコードを見てもらえばわかるので、
ここでは割愛し、主に目玉となる関数だけ取り上げていく。

biofermin2biofermin2

適当にcsv-fileという変数名で編集処理をしたいcsvデータを定義

(defvar csv-file "~/howm/junk/location15-info/17_2021.csv") ; =>CSV-FILE

一時格納しておくハッシュテーブルも適当に定義

(defvar ht (make-hash-table :test #'equal))                 ; => HT

lispを初め大体のプログラミング言語ではデータは０から数え始める。
という事で先程あげたB，D，F，G，Hという列は
1,3,5,6,7となる。その内ハッシュテーブルのキーとして使いたいデータを
:keyに、値として使いたい列データを:valでそれぞれリストでセットする。
cutの引数にあるtitleとuseだが、これは１行目がタイトル行の場合tとなるが、
デフォルトでtに設定してある。今回のcsvデータではタイトル行があるので、
デフォルトのままでいいという事になる。
またuseはそのタイトル行を出力させたい場合にtとするが
デフォルトではnilになっているので出力はされない。

(cut csv-file :to ht :key '(1 3 5) :val '(6 7))

cutで上記のように設定して実行したら
print-htを使ってハッシュテーブル内の状態を確認すると下記の通り
ハッシュテーブルにデータが入っている事がわかる。
上記の表計算ソフトに表示されているデータと合っていると思う。

(print-ht ht)                           ; => 
(("石川県" "金沢市" "青草町") ("36.571525" "136.656136")) 
(("石川県" "金沢市" "相合谷町") ("36.491987" "136.707648")) 
(("石川県" "金沢市" "暁町") ("36.562942" "136.67224")) 
(("石川県" "金沢市" "赤土町") ("36.583352" "136.596634")) 
(("石川県" "金沢市" "浅丘町") ("36.638379" "136.740653")) 
(("石川県" "金沢市" "朝加屋町") ("36.509489" "136.724497")) 
(("石川県" "金沢市" "浅川町") ("36.51673" "136.705331")) 
(("石川県" "金沢市" "浅野本町") ("36.586531" "136.656886")) 
(("石川県" "金沢市" "浅野本町一丁目") ("36.580948" "136.660871")) 
(("石川県" "金沢市" "浅野本町二丁目") ("36.58442" "136.66046")) 
(("石川県" "金沢市" "朝日牧町") ("36.615406" "136.75819")) 
(("石川県" "金沢市" "旭町一丁目") ("36.548614" "136.686241")) 
(("石川県" "金沢市" "旭町二丁目") ("36.554182" "136.683501")) 
(("石川県" "金沢市" "旭町三丁目") ("36.55299" "136.681874")) 
(("石川県" "金沢市" "小豆沢町") ("36.525827" "136.732955")) 
(("石川県" "金沢市" "油車") ("36.557665" "136.656653")) 
以下略
biofermin2biofermin2

上のデータを見てもらえばわかるが、csvのような表型のデータは
重複するデータが非常に多い。

上で言うと、石川県と金沢市はそれぞれ１つあれば十分と感じないだろうか？
少なくとも自分はそう感じた。

イメージとしてはこんな感じ。

こういうのをツリー図あるいは樹形図とも言う。
英語ではまんまtreeと呼ばれるが、ちょうど上の画像を逆さまにすると
石川県の部分が根っこになって、町の部分が葉っぱになるような木のイメージになると思う。

lispのS式はこのtreeと呼ばれる木構造を表現するのにとても有用で、
lispのプログラム自体抽象構文木（AST)と呼ばれる木構造で出来ている。

ちなみに今回作ったようなツリー構造はunion-find treeとかdisjoint sets
と呼ばれるものらしいが、そのあたりのアルゴリズムというか
そういった名前すら知らずに作った。

また上のような図は数学の分野ではグラフと呼ばれる。
グラフというと統計などでの数値を表した折れ線グラフや棒グラフ、円グラフとかを
イメージする人もいるかもしれないが、それとは別に
グラフ理論というものがあってそこと密接に関係がある。

という事で下記の関数でS式に変換してみる。

(defun ht2tree (ht)
  "ハッシュ表内のデータをツリー構造に変換"
  (loop :for (k1 k2 k3) :being the hash-keys :of ht :using (hash-value v)
        :collect (cons k2 (cons k3 v)) :into acc
        :finally (return (cons k1 (group-by acc))))) ; => HT2TREE

実行結果は下記の通り。

(ht2tree ht)                            ; =>
("石川県"
 ("金沢市" ("青草町" "36.571525" "136.656136") ("相合谷町" "36.491987" "136.707648")
  ("暁町" "36.562942" "136.67224") ("赤土町" "36.583352" "136.596634")
  ("浅丘町" "36.638379" "136.740653") ("朝加屋町" "36.509489" "136.724497")
  ("浅川町" "36.51673" "136.705331") ("浅野本町" "36.586531" "136.656886")
  ("浅野本町一丁目" "36.580948" "136.660871") ("浅野本町二丁目" "36.58442" "136.66046")
  ("朝日牧町" "36.615406" "136.75819") ("旭町一丁目" "36.548614" "136.686241")
  ("旭町二丁目" "36.554182" "136.683501") ("旭町三丁目" "36.55299" "136.681874")
  ("小豆沢町" "36.525827" "136.732955") ("油車" "36.557665" "136.656653")
  ("天池町" "36.475802" "136.711451") ("荒屋一丁目" "36.615684" "136.684239")
  ("荒屋町" "36.61465" "136.685684") ("荒山町" "36.565563" "136.784732")
  ("有松一丁目" "36.542192" "136.641574") ("有松二丁目" "36.542978" "136.637864")
  ("有松三丁目" "36.539561" "136.640295") ("有松四丁目" "36.539755" "136.636088")
  ("有松五丁目" "36.53897" "136.63808") ("粟崎浜町" "36.634391" "136.613521")
  ("粟崎町" "36.620711" "136.625269") ("粟崎町一丁目" "36.626146" "136.628321")
  ("粟崎町二丁目" "36.628959" "136.62766") ("粟崎町三丁目" "36.626533" "136.623959")
以下省略

別にツリー構造にしなければ出来ないという話ではないが、
既存のリレーショナル・データベース（RDB）はどれもCSVファイルに
見るような碁盤の目のようなテーブルで管理されている。

ただ、そういった主流とされてきたデータベースの考え方を
見直す試みも以前からいろいろと見られる。

自分もそういう意味合いもあって敢えてメインの流れとは違ったやり方で
今回試してみたというわけだ。天邪鬼なので笑

今回のこのやり方のメリットは重複したデータがかなり削減されるので、
データ容量を比較的小さく保てるという事が挙げられる。

例えばちょうど東京都のデータがあるので比較してみると、
S式ツリーのデータの大きさは244kb
対して、csvでの元データの大きさは557kb
単純に半分以下程度の大きさか。

検索対象の元データがこのように小さく成るので、
検索スピードの面でも多少有利になるかもしれない。
探す範囲が狭くなるので。

ツリー構造とかグラフ構造を使っているという意味では
mongoDBやneo4jといったNoSQLデータベースに通じる
考えだと思うし、面白い分野だと個人的には思っている。
gitとかブロックチェーンもこういうタイプじゃないかな。

すっかり話が脇にそれたのでこの話はここまでにして
本題に戻るとする。

biofermin2biofermin2

本題に戻るため改めて幾何中央値について書くと
ある点から各点までの距離の総和の最小値をもつ点をいう。

大きな問題はなるべく小さく、かつ具体的に考えるといいので、
とりあえず、あるエリアにA,B,C,D,Eの５地点あるとする。

最初にある点をAとするなら
A-B
A-C
A-D
A-E
の距離を調べる。

次にある点をBとするなら
B-Aの距離はA-Bの距離と変わらないので、上で既に求められているから
B-C
B-D
B-E
の距離だけを新たに調べる。

次にCとするなら
上記にC-A,C-Bは同様に既に求められているので、
C-D
C-E
の距離だけを調べる。

次にDとするなら
D-A,D-B,D-Cは既に求められているので、
D-E
の距離だけを求める。

Eについては既に上記で全て求められているので
距離の調査はここで終了となる。

２点間の距離のように選択した順番が関係ないものを
数学では組合せ（combination)という。

この組合せの計算には階乗計算を用いるので、
計算が苦手な自分は昔に書いた専用の関数を使う事にする笑

卑怯な手だと思うかも知れないが、計算という煩わしいもので、
数学が嫌いになるくらいなら、どんどんと計算はコンピューターに
任せてもっと数学の面白い部分にタッチしてた方がいいと
元々数学が嫌いだった自分は思う。プログラミングはそういう
人間にとってまさに楽するための福音なのだ笑

まず階乗計算が必要になってくるが、通常lispの例題では
関数名がfactとかfactorialとして定義される。

ここではよりわかりやすく数学に寄せて！で定義したものを使う。

(defun ! (x)
  "階乗計算factorial"
  (if (= x 0)
    1
    (* x (! (- x 1)))))      ; => !
;; 0!は
(! 0)           ; => 1
;; 1!は
(! 1)           ; => 1
;; 2!は 
(! 2)           ; => 2
;; 3!は
(! 3)           ; => 6

本当は破壊的処理に！を付ける慣習があるが、
ここではあくまで数学的なわかりやすさからそうさせてもらっている。
Common Lispは結構自由です笑

次に順列(permutation)。これは順番が違ったら異なるペアとして
カウントする考え。
定義は_nP_r = \cfrac{n!}{(n - r)!}なので、
定義をlispで書き直すと、

(defun P (n r)
  "Permutaion 順列(異なるn個のものから異なるr個を取り出し並べる順列の数)"
  (/ (! n)
     (! (- n r))))      ; => P

で、最後に組合せ

(defun C (n r)
  "Combination 組み合わせ(n個のものからr個のものを選ぶ組み合わせの数)
A-BもB-Aも同一視。つまり順番は関係ないのが順列との違い。
"
  (/ (! n)
     (! (- n r))
     (! r)))          ; => C

_nC_r = \cfrac{_nP_r}{r!}とも書けるので、順列を使って書くと

(defun C (n r)
  (/ (P n r) (! r)))

こんな感じか。こちらの書き方の方が見た目はスッキリしてる。早速上の例を計算してみると
５個のうち２つを選んだ組合せなので、_5C_2は次のように書く。

(C 5 2)                                 ; =>10

上の例を数えるとまさに１０通り。
答えは合っているが、実はこれらの計算は今回使わない笑
あくまで組合せというものの復習がてらに書いてみた。

今まさに学校の宿題でこの課題を出されている子供たちは
lispのこの定義を使ってサクサクと片付けちゃってね笑

biofermin2biofermin2

今回必要となるのは組合せの数を求める式ではなくて、
組合せパターンを出す関数。
という事で、作ったのが以下のもの。

(defun comb (lst)
  (flet ((pair (l)
	   (let ((key (car l))
		 (rest (cdr l)))
	     (mapcar #'(lambda (x) (list key x)) rest))))
    (mapcon #'pair lst)))               ; =>COMB 

(comb '(a b c d e))                     ; => ((A B) (A C) (A D) (A E) (B C) (B D) (B E) (C D) (C E) (D E))

先程、小さいグループの例で書き出したパターンがまさに出ているのがわかると思う。

biofermin2biofermin2

ちょっと脱線。

最近chatGPTがうんたらってtweetがやたら流れてくるから、
ちょっとchatGPT的にはどうなんだ？と思って聞いてみた。

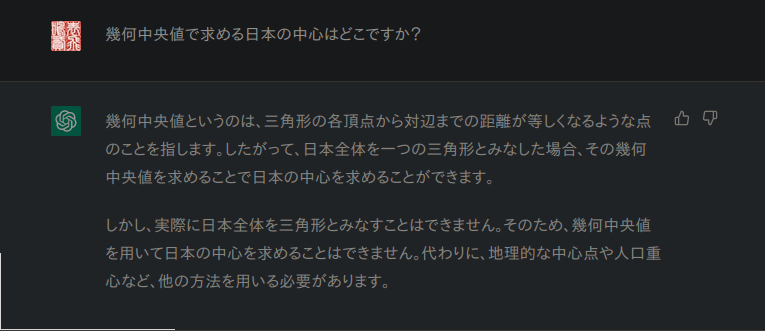
あまり答えになってないなと思ってregenerateしてみたら次の回答が出た。

幾何中央値は、測定した複数の点のうち、その中心点を求める方法の一つです。しかし、日本の中心を定義するためには、その基準が必要です。いくつかの定義が存在しますが、以下にいくつかの代表的なものを紹介します。

国土地理院による定義
国土地理院は、日本の中心点を以下の座標として定義しています。
北緯35度40分0.00秒、東経138度44分0.00秒
この座標は、岐阜県恵那市と長野県諏訪市の境界付近に位置します。

測量による定義
測量によって日本の中心点を求める試みがあります。1989年に行われた測量では、日本の中心点は岐阜県中津川市周辺にあるとされています。

総務省による定義
総務省は、日本の地理的中心を以下のように定義しています。
東京都港区芝公園4丁目2番8号（日本科学未来館内）
この定義は、総務省の定義として一般的に使われることはありませんが、政府関係者が必要とする場合にはこの定義が用いられることがあります。

以上のように、日本の中心点には複数の定義が存在します。幾何中央値を用いた場合には、測定された複数の点の座標を用いて、中心点を求めることができます。ただし、どの定義を用いるかによって、求められる中心点の座標は異なる可能性があります。

他にも日本の中心で調べるといろんな定義による中心は出てくるけど、
結局幾何中央値を使って求めている事例というのはここくらいじゃないかな？多分。

とりあえず、昨年作ったソースコードでは各市区町レベルの幾何中央値は出せるように
してあるとは思うけど、実はまだ４７都道府県全部調べた訳でもないし、
もちろんデータも作ってない。

一体どこが幾何中央値的な日本の中心になるのか楽しみだし、それで求めた値をここに発表したら
いつかchatGPTがその答えを横取りして、誰かに教え出すんだろうな笑

とりあえず、現段階の技術で出来ているのが、各市区町（行政区）レベルでの幾何中央値なので、
次の段階としては都道府県レベルの幾何中央値を出して、
最後に日本の中心となる幾何中央値を出すという流れだけれども、
そういう積み上げ方式ではなく、一気に中心である幾何中央値を求める
という方法も考えられる。
多分、後者の方が精度的には高くなるような気がするが、
如何せんマシンパワーが。。。苦笑

そういう意味でもまずは前者の積み上げ方式で１つ１つ積み上げていきたい。

実は今自分が住んでいる近辺にも日本の中心地を謳っている場所がある。
地の果てみたいなすっごい田舎なんだけど笑
でも、日本の中心に位置する田舎っていうのもなかなかかっこいいと思う笑
そういう意味でも今住んでいるところもいい候補地だとは思う。

biofermin2biofermin2

ちなみに一気にやる手法だけど、
wcコマンドで全国の市区町村丁目の数を調べると
190435からタイトル47行分引くと
19万388箇所あるという話になる。
上に書いた組合せの関数に当てはめてみたが、
見事に答えが返ってこなかった笑
やはり自分のマシンのパワーでは一気に計算するのは難しいようだ。

biofermin2biofermin2

こう言う事を求めて何が便利かふと考えた。
地形的な幾何中央値を求めるなら本来海岸線の点を
基準に考えればいいと思う。
しかし、今回使ってるのは各町村大字丁目の緯度経度なので、
まず第一段階で求まるのは、市区町レベルの行政区の幾何中央値。
次に求まるのが都道府県レベルの幾何中央値。
つまり役場、役所などを設置して統治するのには
山とか川などの障害を考えず、単純な距離だけで言うなら
もっとも各地にアクセスしやすい場所と言える。
そう言う土地であるなら地価としての価値は高い、
乃至上がる可能性があるのでは無いだろうか？
もちろん障害を考慮してないから実際そう単純な話でも無いとは
思うけど、一つの参考にはなるかもしれない。
そんな土地買収する程のお金も無いけどね笑
日本全体の幾何中央値についてはそこに首都を設けるなんて話にもならない
だろうから、本当に自己満足か愛を叫びに行くかの
用途しか無いような気はする笑
まぁ、それでも各都道府県にアクセスするには便利な場所の様な気もする。

biofermin2biofermin2

うーん、ここからはソースコードが自分でも汚いからリファクタリングしなければ
いけないと思っている箇所で、いきなり心理的障壁がグンッと上がって放置してた笑

話を戻すと、何度も連呼して申し訳ないが、幾何中央値というものは
ある点から各点までの距離の総和の最小値をもつ点をいう。

また小さいモデルで考える事にしよう。
ABCDEという５地点があるとして
ある点をAとするなら
各点までの距離というのは
|AB|
|AC|
|AD|
|AE|
となる。
よって点Aを起点とした各点までの距離の総和は
|AB| + |AC| + |AD| + |AE|となる。
これをlisp的に表現すると

(+ |AB| |AC| |AD| |AE|) ;仮に①とする

となる。
lispは前置記法なので、要素数がいくら増えようが+を一番先頭に１つ付けるだけで表現出来るから楽。
学校で習う中置記法の場合、＋記号が加算する要素数の増加に合わせてどんどん増えていく。

;;中置記法
;; 1 + 2 + 3 + 4 + 5 + ...
;;前置記法
(+ 1 2 3 4 5 ...)

学校で習う慣れ親しんだ計算の書き方と違うから気持ち悪さもあるかも知れないが、
このように前置記法には同一の処理記号をまとめられる優れたメリットがある。
小さい事かも知れないけど、これもlispの良さの１つだと思っている。
数列のリストさえあればループ処理を使う事すらなく一発で合計などの
処理計算も出来る。例えば以下の通り。

;; 手で入力していると面倒なので適当に数列を作る関数を作成
;; ここでは仮に1〜100までの数列のリストを作ってみる。

(defun iota (start end &optional (step 1))
  (loop :for i :from start :to end :by step
	:collect i))			; =>IOTA 

;; この通り1〜100までの数列が出来る。
(iota 1 100)				; =>(1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55
 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81
 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100) 

;; 数列のリストの先頭に+記号などの関数を入れたい時はapplyを使う。
(apply #'+ (iota 1 100))		; => 5050
;; 上の式は(+ 1 2 3...100)と同じ意味になる。

まぁ、これ実はloopでcollectの代わりにsumを使えば済む話だけど
あくまで数列のリストをループを使わず一発処理する例をあげたかったので
敢えて面倒臭い事をしている笑

こういった便利な記法があるという事を知った上でまだ++++++++...と
入力し続けたいだろうか？

プログラマーの美徳の1つに怠惰さがある。言葉の響きからあまり良いイメージは持たれないだろうし、
誤解を受けやすい表現ではあるけど、ひたすら++++++...と入力するような時間の無駄を省こうとする考え方はむしろスマートではないだろうか？

そんなの面倒だよな、馬鹿馬鹿しいよな、時間の無駄だよな等感じた人にとって
lisp系言語はうってつけだと思う。

ちなみに前置、中置ときたから後置もあるだろ？と思った方はビンゴ。
Forthというプログラミング言語では後置記法というものを使っている。
あまり詳しくないので、興味がある人は自分で調べてね笑

話を本題に戻すとして次にある点をBとするなら上と同様な形で各点までの距離の総和を求めると

(+ |BA| |BC| |BD| |BE|) ;仮に②とする

点Cを起点とするなら

(+ |CA| |CB| |CE| |CD|) ;仮に③とする

点Dは

(+ |DA| |DB| |DC| |DE|) ;仮に④とする

最後に点Eは

(+ |EA| |EB| |EC| |ED|) ;仮に⑤とする

こうやってあげた総和の最小値を持つ点が幾何中央値となる。
lisp的に書けば

(min ① ② ③ ④ ⑤)

上記の式を計算して仮に最小値が④となれば④はDを基点としているので、
幾何中央値はDとなるという話。

点が５つあって、距離はそれぞれ４つあげているから
5 * 4 = 20
しかし、|AB|も|BA|も距離は同じなので、
組合せで既に求めた通り、距離についてはその半分の１０求めれば済むという話。

そこで組合せパターンのリストを元に各地点間の距離を求めていく必要が出てくる。

このように非常に面倒なプロセスを経なければならないが、
やっている計算自体は足し算だったり掛け算だったりと
さほど難しい話ではないと理解していただけたのではと思う。

biofermin2biofermin2

ソースコードについてはこんがらがった頭でとりあえずプロトタイプで作った事もあり
かなりぐちゃぐちゃなので後回しにして
とりあえず出来た成果物の中身を見てみる事にする。

adr3-石川県.dbの中身は

#.(SB-IMPL::%STUFF-HASH-TABLE (MAKE-HASH-TABLE :TEST (QUOTE EQUAL) :SIZE 3481) 
(QUOTE 
(((1 . 1) . #S(JPMAP::ADR3 :NAME "青草町" :GM NIL :LAT 36.571526 :LON 136.65614 :DIST 45.78487)) 
((1 . 2) . #S(JPMAP::ADR3 :NAME "相合谷町" :GM NIL :LAT 36.491985 :LON 136.70764 :DIST 90.91066)) 
((1 . 3) . #S(JPMAP::ADR3 :NAME "暁町" :GM NIL :LAT 36.562943 :LON 136.67224 :DIST 48.64007)) 
((1 . 4) . #S(JPMAP::ADR3 :NAME "赤土町" :GM NIL :LAT 36.58335 :LON 136.59663 :DIST 68.471466)) 
((1 . 5) . #S(JPMAP::ADR3 :NAME "浅丘町" :GM NIL :LAT 36.63838 :LON 136.74065 :DIST 110.14426)) 
((1 . 6) . #S(JPMAP::ADR3 :NAME "朝加屋町" :GM NIL :LAT 36.509487 :LON 136.7245 :DIST 89.66744)) 
((1 . 7) . #S(JPMAP::ADR3 :NAME "浅川町" :GM NIL :LAT 36.51673 :LON 136.70534 :DIST 76.004105)) 
((1 . 8) . #S(JPMAP::ADR3 :NAME "浅野本町" :GM NIL :LAT 36.586533 :LON 136.65689 :DIST 49.73026)) 
((1 . 9) . #S(JPMAP::ADR3 :NAME "浅野本町一丁目" :GM NIL :LAT 36.580948 :LON 136.66087 :DIST 48.38626)) 
以下省略

頭の１行目はこのデータがハッシュテーブルという事を示していて、test条件やサイズなどが書かれている。
QUOTE以下が肝心のハッシュテーブルの中身のデータで、
一番左の(1 . 1)というconsセルはハッシュテーブルのkey部を意味していて、
左のcar部がより上位の行政区番号、
つまり１なのでここでは金沢市を意味している。右のcdr部は町名などの番号。
次にドットの右側に来る#Sの部分だがSはstructureつまり構造体の意味で
ハッシュテーブルのvalue部に構造体が格納されている事を表している。
先程の町大字名番号の１に該当するのが青草町である事を表している。
:GMだがこれはgeometric medianつまり幾何中央値の事。とりあえず町毎の幾何中央値は
ないのでNILが入っている。
次の:LATは緯度 :LONは経度　それぞれ英語のlatitude,longitudeを表している。
最後の:DISTはdistanceの略で青草町を基点とした距離の総和が入っている。

つまり上記の事をまとめるとハッシュテーブルのデータの中身は

 ;;       　　   key部                                          value部
((行政区番号 . 町大字名番号) . #構造体(:NAME 町大字名 :GM 幾何中央値 :LAT 緯度 :LON 経度 :DIST 距離の総和))

という構造となっている。スペースの都合上データの大部分を省略しているが、
県内各行政区内の大字町丁目毎のデータが入っている。

adr2-石川県.dbの中身は

#.(SB-IMPL::%STUFF-HASH-TABLE (MAKE-HASH-TABLE :TEST (QUOTE EQUAL) :SIZE 19) 
(QUOTE 
((1 . #S(JPMAP::ADR2 :NAME "金沢市" :GM (1 . 281) :LAT 36.564156 :LON 136.65309 :DIST 7.2879996)) 
(2 . #S(JPMAP::ADR2 :NAME "七尾市" :GM (2 . 48) :LAT 37.05013 :LON 136.95277 :DIST 8.517816)) 
(3 . #S(JPMAP::ADR2 :NAME "小松市" :GM (3 . 215) :LAT 36.397835 :LON 136.45349 :DIST 10.001682)) 
(4 . #S(JPMAP::ADR2 :NAME "輪島市" :GM (4 . 154) :LAT 37.309288 :LON 136.82997 :DIST 10.883964)) 
(5 . #S(JPMAP::ADR2 :NAME "珠洲市" :GM (5 . 61) :LAT 37.458473 :LON 137.2508 :DIST 15.7237425)) 
(6 . #S(JPMAP::ADR2 :NAME "加賀市" :GM (6 . 51) :LAT 36.303623 :LON 136.33604 :DIST 12.490096)) 
(7 . #S(JPMAP::ADR2 :NAME "羽咋市" :GM (7 . 56) :LAT 36.901608 :LON 136.80272 :DIST 6.997764)) 
(8 . #S(JPMAP::ADR2 :NAME "かほく市" :GM (8 . 2) :LAT 36.736248 :LON 136.71361 :DIST 6.6486697)) 
(9 . #S(JPMAP::ADR2 :NAME "白山市" :GM (9 . 227) :LAT 36.504974 :LON 136.56865 :DIST 7.951446)) 
以下省略

１行目は上と同じくハッシュテーブルのTEST条件やサイズ
QUOTE以下がハッシュテーブルに格納したデータ。
最初のデータの左のcar部に入っている１は行政区番号
次に右のcdr部はやはり構造体でその行政区の名前が
金沢市であり、幾何中央値がkey部が(1 . 281)となっている町を表している。
ちなみに(1 . 281)に該当する町を調べたら香林坊二丁目と出てきた。
金沢で育った人間としては納得の結果かな。かなりいいポイントを抑えている気はする。
実際の地図を検索して見ると。。。

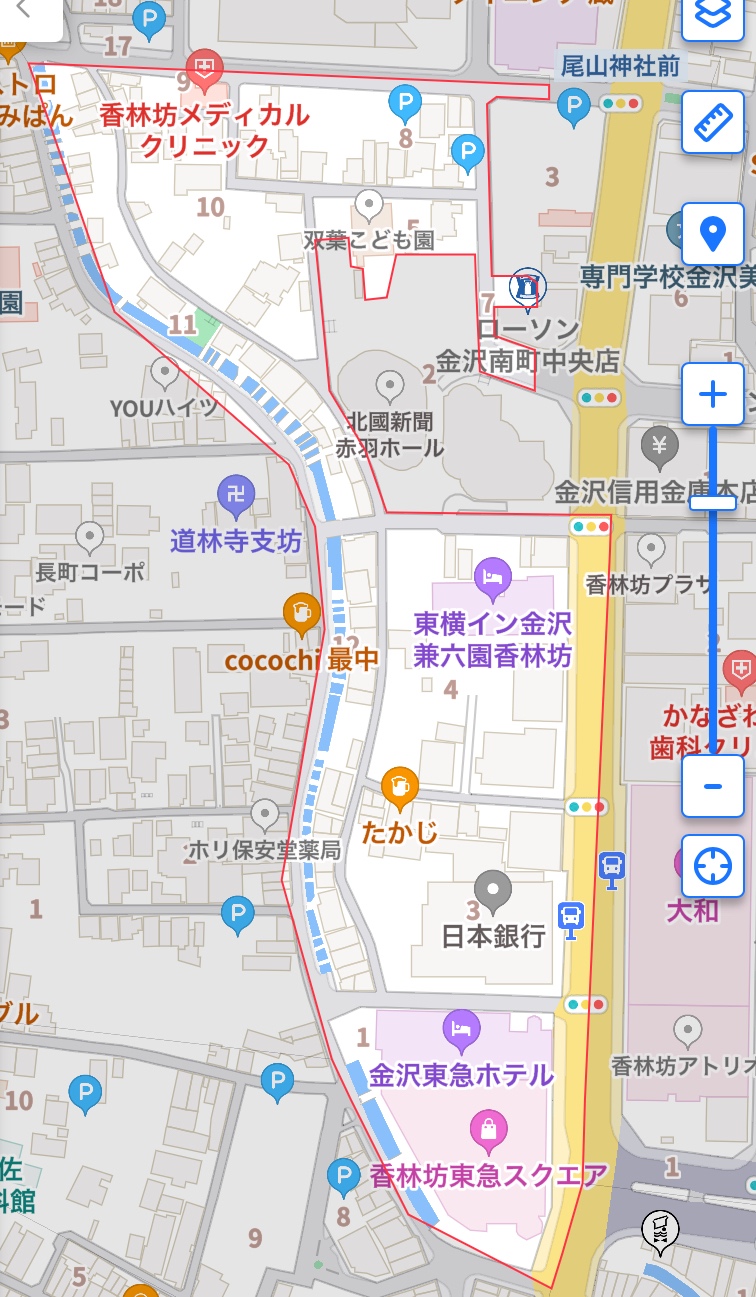
赤線の枠内がそれ。日銀しっかり抑えてますね笑　手堅い。
赤枠から外れているけど、赤枠に囲まれている北國新聞社も
いち早く地元の情報をキャッチする上では抜群な立地をしていると言える。
渋谷にもある109の地方初出店の店舗がかつてここにもあったが、
今は東急スクエアに改称されたようだ。
よくよく眺めてると、cocochi最中なる店が。
この店の方は金沢市の中央である事からこの店名にしたのだろうか？
何か自分で中央値みたいなものを求めたのだろうか？
赤枠から少し外れているがちょっと気になった。

本題に戻るが次に緯度、経度、最後にその最小となる総和の距離が入っている。

つまりまとめると以下の通りのデータ構造となっている。

;;    key部　　　　　　value部
((行政区番号 . #構造体(:NAME 行政区名 :GM 幾何中央値 :LAT 緯度 :LON 経度 :DIST 距離の総和の最小値))

こちらもデータを省略しているが、県内の各行政区のデータが格納されている。
ハッシュテーブルのデータサイズが１９なので、つまり石川県下には１９の行政区があるという事になる。

このようにこのプログラムで現在求められているのは各行政区の幾何中央値まで。
例えば石川県の幾何中央値はどこかという事に関してはここで作成されたデータを
元に更に同様の計算を積み上げていく必要があるという事になる。
現時点ではまだそこまではやっていない。
ましてや、日本の幾何中央値となると更にそのもう一段上に積み上げる必要がある。

この先については自分自身だいぶお休みしてたので、
復習しながら積み上げて行きたい。出来ればもっと綺麗にリファクタリングも進めたい。

biofermin2biofermin2

作業が全く進んでないので再び脱線。
googleのbardも日本語対応してなかなかいいというので、
ちょっと脱線して幾何中央値について訊いてみた。
Bardの回答は以下の通り。

幾何中央値とは、ユークリッド空間内の点の集合の中央値です。
点の集合までの距離の合計を最小化する点です。
これは、1 次元データの距離の合計を最小化する特性を持つ中央値を一般化し、
より高い次元で中心的な傾向を提供します。
幾何中央値は、統計、機械学習、コンピューターグラフィックスなどの多くの分野で使用されています。たとえば、統計では、離散データの中央値を見つけるために使用できます。
機械学習では、クラスタリングアルゴリズムの一部として使用できます。
コンピューターグラフィックスでは、画像のアンシャープマスクを作成するために使用できます。
幾何中央値を見つける方法はいくつかあります。最も一般的な方法は、最小二乗法を使用することです。最小二乗法は、点の集合までの距離の合計を最小化する点を探します。
もう 1 つの方法は、動的計画法を使用することです。
動的計画法は、点の集合までの距離の合計を最小化する点を見つける再帰的なアルゴリズムです。
幾何中央値は、データの中心的な傾向を示すために使用できる強力なツールです。
統計、機械学習、コンピューターグラフィックスなどの多くの分野で使用されています。

ChatGPTはすぐデタラメな感じの印象を受けたのに対して、
Bardの方はそれっぽい感じで書かれている印象がある。
この中でも個人的には最小二乗法と動的計画法というものが
まだよくわかってないので、ちょっと調べてみたいと思った。

もしかしたら今までやっていたやり方よりもよりスマートな
アルゴリズムなのかもしれない。

Bardなかなか使えそう。

次は英語で訊いてみて、それを日本語に翻訳してもらった内容が以下の通り。

幾何中央値とは、ユークリッド空間内の離散的なサンプル点の集合の中央値です。
サンプル点までの距離の合計を最小化する点です。
これは、1 次元データの距離の合計を最小化する特性を持つ中央値を一般化し、
より高い次元で中央傾向を提供します。
1 中央値、空間中央値、ユークリッドミニサム点、またはトルチェッリ点とも呼ばれます。

幾何中央値は、統計学では位置の重要な推定量であり、
L1 推定量（L1 ノルム以降）としても知られています。
また、施設配置の標準的な問題でもあり、輸送コストを最小化するために
施設を配置する問題をモデル化します。
より一般的な k 中央値問題では、各サンプル点からその最も近い中心までの
距離の合計を最小化する k 個のクラスター中心の場所を求めます。
点が線または曲線に一般化される場合、最適なソリューションは絶対偏差の最小値を使用して見つかります。

幾何中央値を使用する方法の例をいくつか示します。

  • 統計では、幾何中央値を使用してデータセットの中央傾向を見つけることができます。
    これは、正規分布していないデータに役立ちます。
  • 機械学習では、幾何中央値を使用してデータポイントをクラスタリングできます。
    これは、互いに類似したデータポイントのグループを見つけるために使用できます。
  • コンピューターグラフィックスでは、幾何中央値を使用して画像のノイズを除去できます。
    これは、ノイズのセット内の幾何中央値を見つけることで実行できます。

幾何中央値は、さまざまな問題を解決するために使用できる強力なツールです。
さまざまな分野で使用できる用途の広いツールです。

上の日本語で訊いたものとダブっている内容もあるが、

また、施設配置の標準的な問題でもあり、輸送コストを最小化するために
施設を配置する問題をモデル化します。

という箇所は既に自分も記述している内容と合致するかなと感じた。

biofermin2biofermin2

動的計画法はwikipediaから抜粋すると

対象となる問題を複数の部分問題に分割し、
部分問題の計算結果を記録しながら解いていく手法

とある。memoize的な考え方だと思うが、
そういう意味では自分もこういう単語を知らずに
ハッシュテーブルで計算結果を活用して再計算しているので、
既にやっていると言えばやっている話。
特に難しい話でもないという印象。

最小二乗法の方は

測定で得られた数値の組を、適当なモデルから想定される1次関数、
対数曲線など特定の関数を用いて近似するときに、想定する関数が測定値に対して
よい近似となるように、残差平方和を最小とするような係数を決定する方法
あるいはそのような方法によって近似を行うことである。
簡潔に言うと、誤差を伴う測定値の処理において、その誤差の二乗の和を
最小にするようにし、最も確からしい関係式を求める方法である。

とある。簡潔に言うとと書かれている以下の文が個人的にはちょっと
わかるような気もした。三平方の定理だと
二乗の和の平方根でユークリッド距離を求めたりする訳だが、
どうせその中の最小値を求めるなら別に平方根しなくてもいいんじゃないか？
という考え方からだと思う。実際自分もそれで一度計算してみたが、
同じ結果になるかと思いきや意外とそうでもなかった笑
平方根の計算を省略する分、計算数は減るから処理速度も多少
速くなると思ったが、結果にずれが生じたため結局使わなかった。
わずかな誤差だとは思うけど、なぜそういうズレが生じたのかも
ちょっと理解出来なかった。

間違った事言ってたらご指摘下さい。

つまり、まとめると動的計画法はそんな名前が付いてるとは知らずに既にやってたし、
そんな大層な名前を付けるような話でもない気がしてる。
最小二乗法もそんな名前が付いてるとは知らずにやったものの計算結果に
誤差が生じたので、採用しなかった。ただ、正攻法よりも計算処理を
一段省いた分、計算速度は速くなるとは思う。