バーンサイドの数え上げ補題
binomialsheep概要
対称性を考慮した数え上げの練習です。
後日Qiitaの記事になるので、急じゃない人は今読まなくてもいいです。
このスクラップボックスでは最終的にABC198 F - Cube（diff2769）を解きます。
binomialsheep用語説明（書きかけ）
巡回置換型
任意の置換は、互いに共通の文字を含まない巡回置換の積に一位に分解される。
巡回置換の長さを並べた列を、その置換の型（巡回置換型）と呼ぶ。
配置
集合Xから集合Yへの写像全体からなる集合をY^Xとする。
Y^Xの元fを配置と呼ぶ。
fは、|X|個のものを|Y|個の部屋に配る配り方の1つに対応している。
binomialsheep円順列
回転して同じものは同一視します。
（※反転は同一視しないことに注意）
黒石と白石が合わせて6個ある。円形に並べる並べ方は何個あるか？
素朴な数え上げ
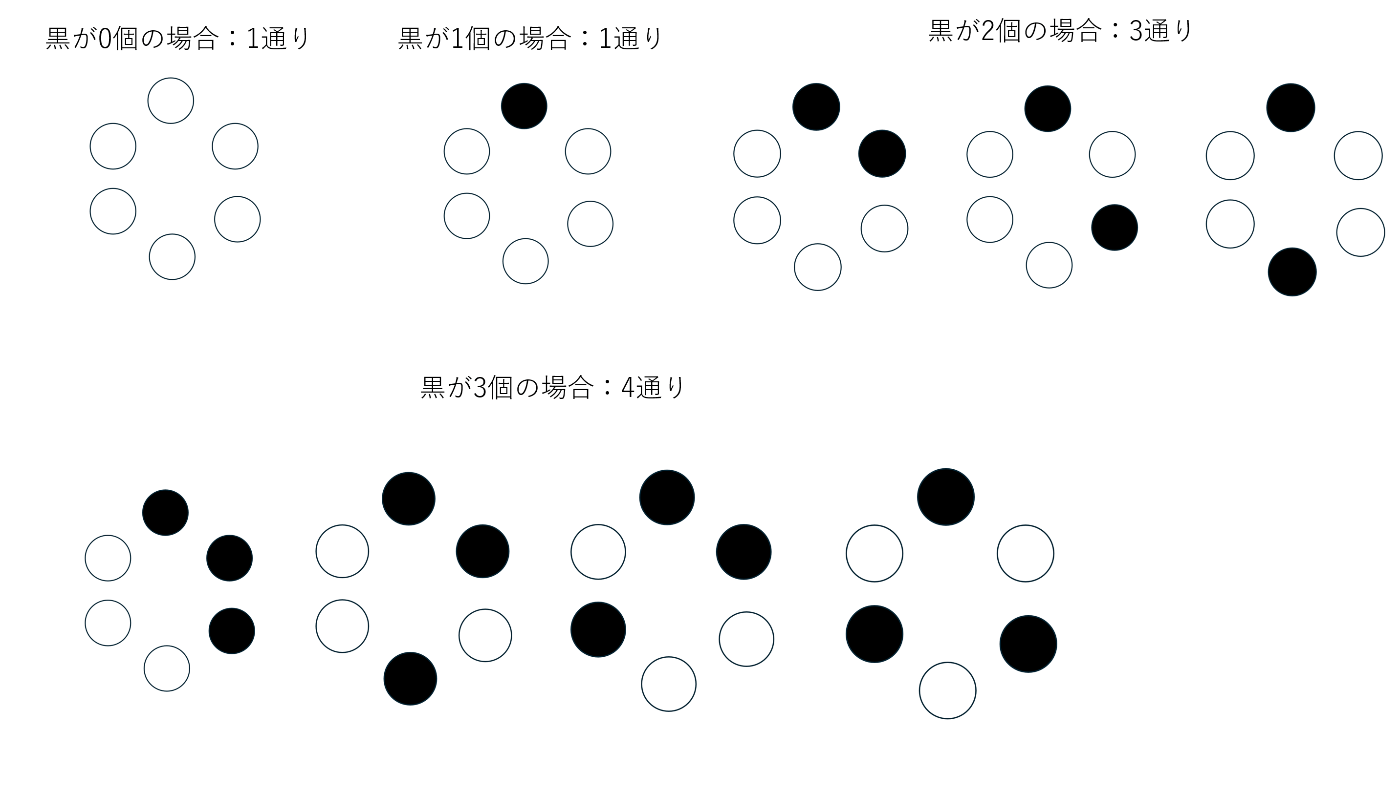
黒石の個数ごとに数えてみます。
黒が4, 5, 6個の場合は対称性よりそれぞれ3, 1, 1通りなので、合計14通りです。
バーンサイドの補題を使った回答１
同一視する操作（|G|）は、0°回転（単位元）から300°回転までの6個です。
①0°回転（単位元）
任意の並べ方について、0°回転しても不動です。
それぞれ黒色か白色なので、並べ方は64通りあります。
②60°回転
60°回転しても不動なのは、全て黒か全て白の2通りです。
③120°回転
120°回転の場合は、黒と白が交互に並ぶ場合も不動なので4通りです。
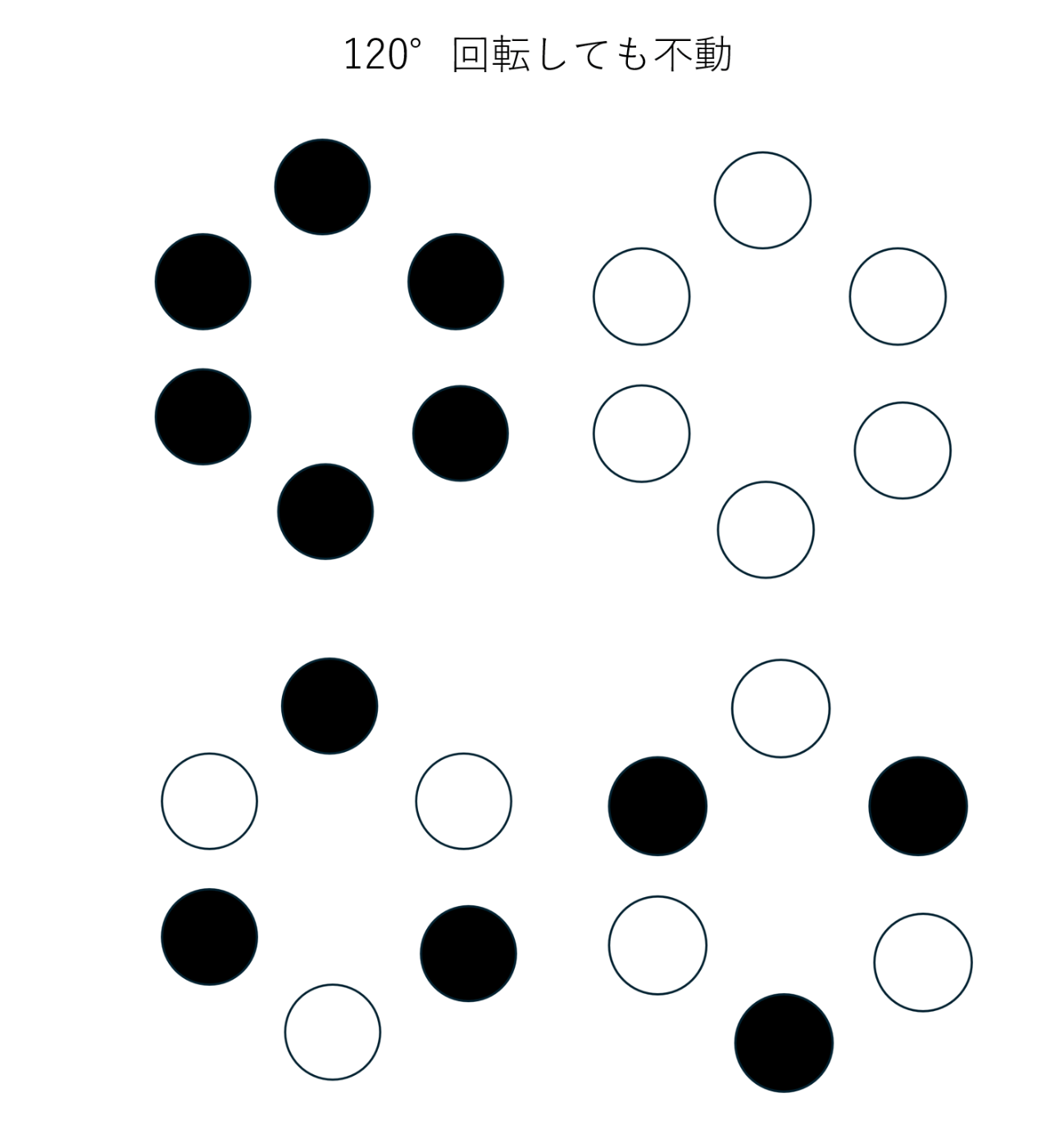
④180°回転
180°回転の場合に不動なのは、以下とその白黒反転なので8通りです。
⑤⑥240°回転、300°回転
対称性よりそれぞれ4通り、2通りです。
公式に代入
よってバーンサイドの補題より、
1/6 * (64+2+2+4+4+8) = 14通り
と求まります。
参考
巡回置換型
回答１では確かに求まりましたが、各操作に対して不動な個数を考察する必要があるようではあまり嬉しくないですね。
突然ですが、各石に数字を振った場合、120°回転は以下のように「1を3があった位置に、2を4があった位置に、……、6を2があった位置に」移動する操作といえます。
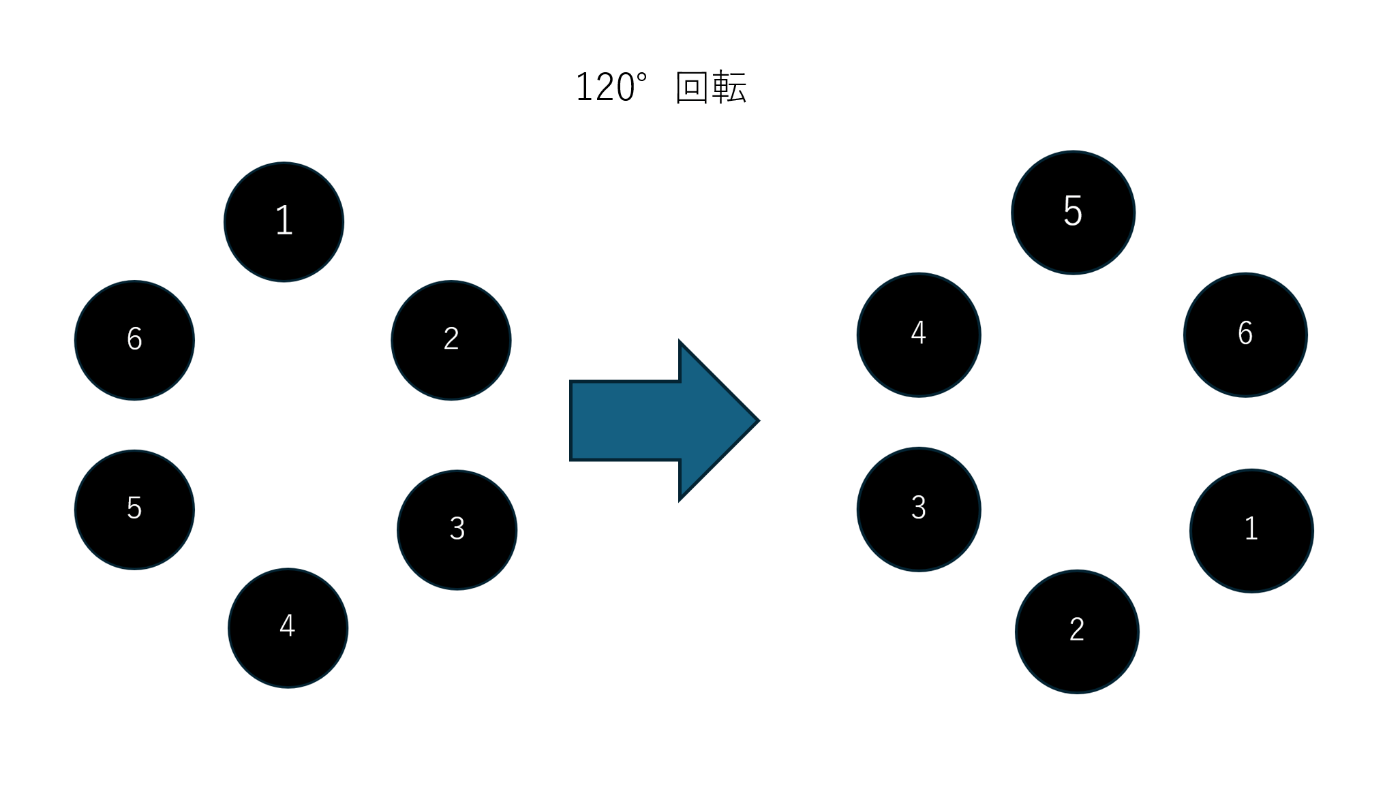
このような操作を置換といい、以下のように表記します。
この置換を眺めていると、おぼろげながら「1→3→5→1→……」「2→4→6→2→……」という構造が見えてきます。この
を巡回置換といい、任意の置換は共通の文字を含まないいくつかの巡回置換の積として一意に表せすことができることが簡単に証明できます。
巡回置換の積を(1 3 5)(2 4 6)のように表します。
また、「巡回置換の積について、長さkの巡回置換がいくつあるか」を巡回置換型といい、
可視化すると分かりやすいかもしれません。
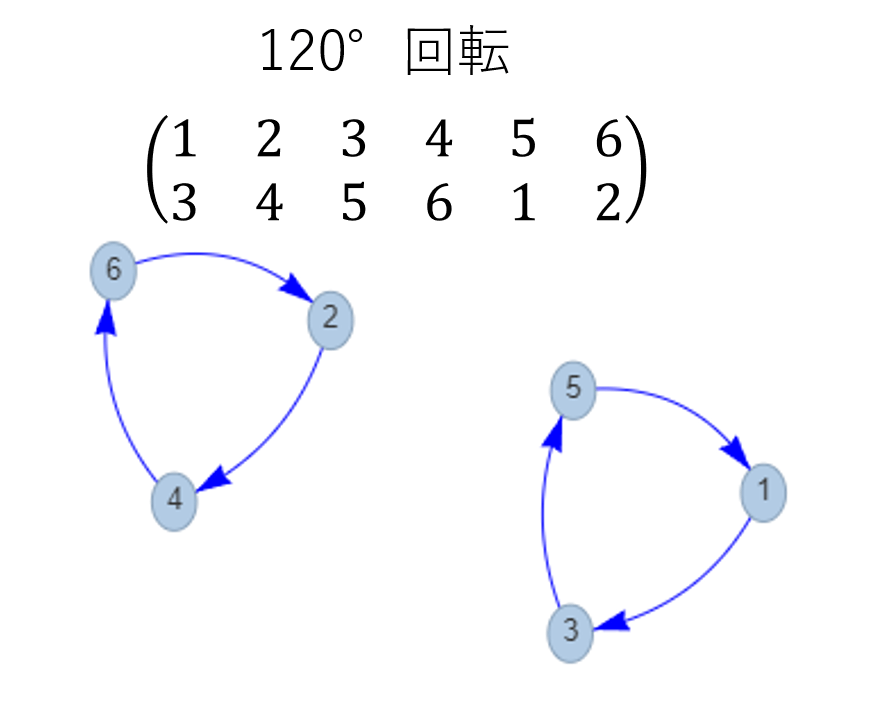
参考
グラフ可視化用の自作ビジュアライザ
自作です。置換を可視化したい場合、例えば
6
1 2 3 4 5 6
4 5 6 1 2 3
と入力して、入力形式を「有向」「辺配列(T)」にすれば良いです。
バーンサイドの補題を使った回答２
巡回置換型の考え方を使うと、より機械的に解けます。
0°～180°回転を置換の見方で可視化すると以下のようになります。
例えば120°回転の場合、不動になるためには(1 3 5)は同じ色である必要があり、(2 4 6)は同じ色である必要があります。つまり「(1 3 5)を何色にするか」「(2 4 6)を何色にするか」で4通りです。
同様に0°から300°まで数えれば1/6 * (64+2+2+4+4+8) = 14通りと求まります。
M色の石が合わせて6個ある。円形に並べる並べ方は何個あるか？
色を2色からM色に一般化してみます。
①0°回転（単位元）
巡回置換型は
②60°回転
巡回置換型は
③120°回転
巡回置換型は
④180°回転
巡回置換型は
⑤⑥240°回転、300°回転
対称性より明らかです。
よって
OEISにも載っています。
赤石が2個、青石が2個、緑石が2個
色の個数が決まっている場合です。
これもバーンサイドの補題で解くことができますが、それぞれの石が2個しかないので、巡回置換型が
①0°回転（単位元）
巡回置換型は
6C2 * 4C2 = 90通り
②60°回転
巡回置換型は
0通り
③120°回転
巡回置換型は
0通り
④180°回転
巡回置換型は
どの巡回置換にどの色を割り当てるか3!で6通り
⑤⑥240°回転、300°回転
0通り
バーンサイドの補題より96/6 = 16通りです。
binomialsheep数珠順列
黒石と白石が合わせて6個あり、回転や反転させても同じものは同一視する
回転が6個、反転が6個ある
- 0°回転：64通り
- 60°回転：2通り
- 120°回転：4通り
- 180°回転：8通り
- 240°回転：4通り
- 300°回転：2通り
- 反転１：8通り
- 反転２：16通り
- 反転３：8通り
- 反転４：16通り
- 反転５：8通り
- 反転６：16通り
1/12 * 156 = 13通り
赤石2個、青石2個、緑石2個を並べる
- 0°回転：90通り
- 60°回転：0通り
- 120°回転：0通り
- 180°回転：6通り
- 240°回転：0通り
- 300°回転：0通り
- 反転１, 4, 5：6*3通り
- 反転２, 4, 6：6*3通り
1/12 * 132 = 11通り
3色で合わせて3個ある場合
3つとも同じ色：3通り
2個だけ同じ色：6通り
3つとも違う色：1通り
-
0°回転：27通り
-
60°回転：3通り
-
120°回転：3通り
-
反転１：9通り
-
反転２：9通り
-
反転３：9通り
1/6 * 60 = 10通り
binomialsheep立方体採色
3色に塗り分ける
- ①単位元：3^6通り
- ②面の90°回転：動くのは4面（27通り）
- 3面×2方向
- ③面の180°回転：回転する対面2組が同じ色ならいい（81通り）
- 3面×1方向
- ④頂点の120°回転：3つの面が入れ替わる（9通り）
- 4頂点×2方向
- ⑤辺の180°回転：27通り
- 6辺×1方向
1/24 * (729 + 6 * 27 + 3 * 81 + 9 * 8 + 6 * 27) = 57通り
M色に塗り分ける
1/24 * (M^6 + 3 * M^4 + 12 * M^3 + 8 * M^2)通り
ABC198 F - Cube
①単位元
- a+b+c+d+e+f=S
②1組の4面がrotateする - (1,2,3,4,5,6)→(2,6,3,4,1,5)
- 4a+b+c=S
③2組の2面がrotateする - (1,2,3,4,5,6)→(6,5,3,4,2,1)
- 2a+2b+c+d=S
④2組の3面がrotetaする - 3a+3b=S
⑤1組の2面がrotateし、1組の4面がrotateする - 4a+2b=S
他の正多面体の場合
binomialsheep参考文献
TODO：読む