アルゴリズムイントロダクション第11章「ハッシュ表」

 アルゴリズムイントロダクション第11章「ハッシュ表」insert, search, deleteだけができればよい効率的なデータ構造を考える。

ハッシュ表は、適切な仮定の下で平均O(1)でこれらの操作が可能であり、最悪Θ(n)だが、実用的には高速で優れている。
「衝突した時にどうするか」
チェイン法
オープンアドレス法
線形走査法
ダブルハッシュ法
独立一様置換ハッシュ法

「どんなハッシュ関数を使うか」
除算法
乗算法
ランダムハッシュ法
万能ハッシュ関数

暗号学的ハッシュ

binomialsheep

 11.1 直接アドレス表 練習問題
 11.1-1：get_max長さがmの直接アドレス表Tによって表現された動的集合Sを考える。

Sの最大要素を発見する手続き：降順に非NILが見つかるまで走査

最悪時の性能：Θ(m)

 11.1-2：ビットベクトルで表現bool search(int k) { return (bit >> k) & 1; }
void insert(int k) { bit |= 1 << k;
void erase(int k) { bit &= ~(1 << k); }
vector<uint64_t>のようにすれば長さを拡張できる。

 11.1-3チェイン法みたいに双方向連結リストを持つ？

deleteがO(1)でできる。searchの場合は（存在すれば）先頭のポインタを返すことにする。

 11.1-4// キーkeyがqueの何番目にあるか
int pos[9999999];
// 今テーブルに存在する要素
vector<int> stack;

bool search(int key) {
    return pos[key] < stack.size() && stack[pos[key]] == key;
}
void insert(int key) {
    if(serach(key)) return;
    pos[key] = stcck.size();
    stack.push_back(key);
}
void erase(int key) {
    stack[pos[k]] = stack.back();
    pos[stack.back()] = pos[k];
    stack.pop_back();
}
類似で、初期化する代わりに定数倍が軽いバージョン。集合内の要素を一様ランダムで高速に取り出せるので、AHCの有効な近傍管理などに便利。

参考：[0,n)の整数の集合を管理する定数倍が軽いデータ構造

binomialsheep

 11.2 ハッシュ表 練習問題
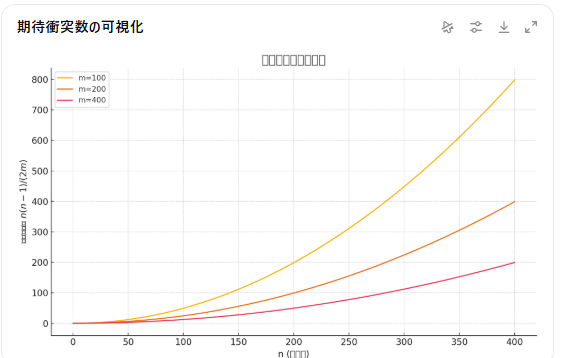
 11.2-1 衝突回数の期待値n := キーの個数, m := 配列のサイズ, T := 配列, h := ハッシュ関数
衝突しているキーのペアの集合のサイズの期待値を求める。

あるキーのペアki, kj (i≠j)が衝突する確率は1/mで、キーのペアはnC2個あるので、期待値の線形製よりn(n-1)/2m。

 11.2-2 チェイン法の例

 11.2-3 チェイン方式をソート済みリストにすると速くなるか？ソート済みの双方向連結リストの場合、高速に二分探索できないので漸近的には速くならない。

成功探索：変わらない

失敗探索：走査中に打ち切れるので定数倍が軽くなる

挿入：ソート済みになるように挿入するので漸近的に悪化する

削除：変わらない

ソート済みの動的配列にした場合、成功探索と失敗探索は速くなるが、削除がO(1)でできなくなる。

 11.2-4 メモリ管理？

 11.2-5鳩ノ巣原理。

 11.2-6　一様ランダムな要素選択while(true) {
    int pi = rand(1, m) // パケットを選ぶ
    int li = rand(1, L) // チェイン内のインデックスを「Lまでの中から」選ぶ
    if(packet_size(pi) < li) continue;
    // 受理
}

 一様性1回の試行で、全ての要素は確率1/mLで選ばれる。

 期待実行時間選ばれるmLのうち有効なキーはn個なので、1試行あたの受理確率はn/mL = α/L。

よって受理されるまでの試行回数の期待値はL/α。

1試行あたりの実行時間は、
受理されない確率(1-α/L) * O(1)
受理される確率(α/L) * O(L)

の和で、O(1 + α)。

よって求める実行時間はO(L(1+1/α))。

binomialsheep

 11.3 ハッシュ関数 練習問題
 11.3-1まずハッシュ値で比較して、一致する場合だけ実際の文字列比較を行う。

文字列比較は衝突した時しか行われないので、平均的には高速
応用：ローリングハッシュで、2種類のハッシュを持っておくとよりハッシュ衝突率が下がる

 11.3-2int h = 0;
for(auto c : str) h = (h * 128 + c)  mod m;
retrun h;

 11.3-3(2^p)^i ≡ 1^i = 1 (mod 2^p - 1)

なので、k ≡ Σxi (mod 2^p - 1)になり、置換しても同じハッシュ値になってしまう。
パスワード検証、文字列検索、データのチェックサムなど多くの例で好ましくない。

 11-3-4import math
import pandas as pd

A = (math.sqrt(5) - 1) / 2
m = 1000
keys = [61, 62, 63, 64, 65]

# ハッシュ値計算
hash_values = {}
for k in keys:
    frac_part = (k * A) % 1
    h_k = int(m * frac_part)
    hash_values[k] = h_k

import ace_tools as tools
df = pd.DataFrame({
    "Key": hash_values.keys(),
    "Hash value h(k)": hash_values.values()
})

tools.display_dataframe_to_user(name="Multiplication Method Hash Values", dataframe=df)
k = 61, 62, 63, 64, 65

h(k) = 700, 318, 936, 554, 172

 11.3-5要勉強

 11.3-6

binomialsheep

 11.4 オープンアドレス法 練習問題
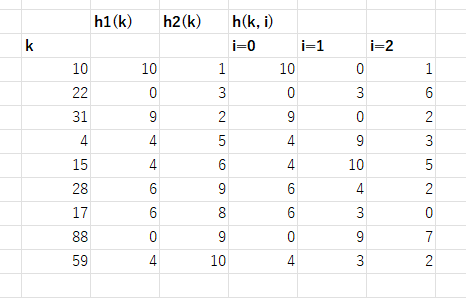
 11.4-110, 22, 31, 4, 15, 28, 17, 88, 59

m = 11

 線形探査法ハッシュ関数：h(k,i)= (k+i) mod11

 ダブルハッシュ法h1(k) = k mod 11

h2(k) = 1 + (k mod 10)

h(k, i) = [h1(k) + i * h2(k)] mod 11

 11.4-2insertだけ注意。

DELTEDを見つけたら位置を記録しておくけど、searchは続ける（重複があるかもしれないので）。重複がない（NILに到達する）ことを確認したら、記録しておいたDELETED（なければNIL）の位置に挿入する。

 11.4-3定理11.7, 11.8を使う。

α=3/4の場合、4, 4/3 ln4(≒1.848）

α=7/8の場合、8, 8/7 ln8(≒2.377）

 11.4-4
 11.4-5「a + ib mod mが何個の値を取るか」はm / gcd(b, m)個というやつ。

時計の針を何個ずつスキップする場合が12か所全て辿るかという話。

 11.4-6
\frac{1}{1 - \alpha} = 2 \cdot \left( \frac{1}{\alpha} \ln\left( \frac{1}{1 - \alpha} \right) \right)
の数値解を求めればよく、α ≒ 0.715らしい

binomialsheep

5 実用における考察 練習問題何も分かんないのでChatGPTの答えだけ張る

5-1

5-2

5-3合ってるか怪しい

binomialsheep

 章末問題
 11-1 ハッシュ法に現れる探査列長の上界
 a最初のp個が埋まっている確率の上界を求めればよい。

n≦m/2よりどの枠も確率1/2未満でしか埋まっていないので、最初のp個全て埋まっている確率は

高々(1/2)^p。よって示された。

 bPr{Xi>2lgn}≦2^(-2lgn)=(2^lgn)^-2 = 1/n^2

 cボンフェローニ不等式

Pr{X>2lgn}≦ΣPr{Xi>2lgn} = n * O(1/n^2) = O(1/n)

 dギブ

 11-2 静的集合の探索
 a前処理でソートしておけば二分探索でO(lg n)

 bm>nを仮定する。

探索失敗の平均探索回数はm/(m-n)。

これをO(log n)にしたい。

m/(m-n)≦c log n（cは正定数）

m-n ≧ m/(c logn) = Ω(n / log n)。

 11-3 チェイン法における枠数の上界
 aサイコロをn回投げてk個がある特定の目になるのと同じ。独立試行n回の二項分布。

 bPk = 「どこかの枠がちょうどk個で、それ以外はk個以下」≦「どこかの枠がちょうどk個」≦ nQk。

最後のはブールの不等式で、

Pr(UAi)≦ΣPr{Ai}=nQk。

 cdetodo

 11-4 ハッシュ法と認証
 a

 b

 c

 d

アルゴリズムイントロダクション第11章「ハッシュ表」

11.1 直接アドレス表 練習問題

11.1-1：get_max

11.1-2：ビットベクトルで表現

11.1-3

11.1-4

11.2 ハッシュ表 練習問題

11.2-1 衝突回数の期待値

11.2-2 チェイン法の例

11.2-3 チェイン方式をソート済みリストにすると速くなるか？

11.2-4 メモリ管理

11.2-5

11.2-6 一様ランダムな要素選択

一様性

期待実行時間

11.3 ハッシュ関数 練習問題

11.3-1

11.3-2

11.3-3

11-3-4

11.3-5

11.3-6

11.4 オープンアドレス法 練習問題

11.4-1

線形探査法

ダブルハッシュ法

11.4-2

11.4-3

11.4-4

11.4-5

11.4-6

11.5 実用における考察 練習問題

11.5-1

11.5-2

11.5-3

章末問題

11-1 ハッシュ法に現れる探査列長の上界

a

b

c

d

11-2 静的集合の探索

a

b

11-3 チェイン法における枠数の上界

a

b

cde

11-4 ハッシュ法と認証

a

b

c

d

11.1 直接アドレス表練習問題

11.2 ハッシュ表練習問題

11.2-6　一様ランダムな要素選択

11.3 ハッシュ関数練習問題

11.4 オープンアドレス法練習問題

11.5 実用における考察練習問題