AttentionとKernel smootherの関係について

「AttentionはKernel Smootherとみなせる」という表現がされていたが、パッと見何を言っているのかわからなかったので整理しておく。
結論から言うと、関係があるというよりは数学的形式が同じであるということを主張しているのだと思われる。

Kernel Smoothingとは信号処理において、ノイズを含む信号を平滑化する手法で、時系列的に近い観測点のデータを混ぜることで平滑化をおこなう。形式的には以下のように表される。

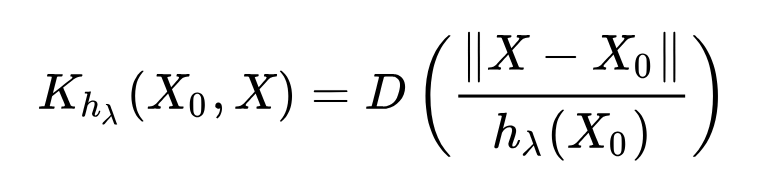
これが意味するところは、距離関数Dを定義しておき、距離が近いものほど計算結果への寄与を大きくする役割がある。見る範囲を固定のwindowで絞ると畳み込みフィルターと等価になる。

上記の式で、

1. Y(X_i) \rightarrow V_i
2. \kappa(X_0, X_i) \rightarrow \kappa(Q_i, K_j)

と置き換えるとSoftmax Attentionの式と形式的に同じになる。

Valueベクトル V_j が観測点に対応し、QKの行列積が V_j の寄与率に相当する。
Kernel Smootherは入力変数空間での距離に基づくkernelを採用しているが、Attentionでは内積に基づくkernelを採用している。

入力ベクトルXをQ, K, Vにマッピングせずに直接Attentionブロックに入力するとSmootherっぽく見えるようになる。

Reference

1. https://en.wikipedia.org/wiki/Kernel_smoother