What are Diffusion Models?

Text: What are Diffusion Models?

一言で

拡散モデル(DDPM, DDIM)について解説した記事。

DDPMとは

生成モデルの一種で、入力データにノイズを繰り返し付加する過程（順方向の伝搬）と、ノイズから元のデータを復元する過程（逆方向の伝搬）からなる。データの生成時は、ある分布（通常Gaussian）からサンプルしたノイズを元に、逆方向の過程を繰り返し適用することで生成する。

1. 順方向の伝搬: 入力データのエネルギーを減衰させながら、ある割合のノイズを付加する過程を繰り返し適用する（典型的にはN=1000）。最終的にガウスノイズと見做せるまで繰り返す。
2. 逆方向の伝搬: NNによって付加されたノイズを予測し、キャンセルすることで信号を復元する過程。順方向の伝搬を逆に辿る。

NNのアーキテクチャはUnetベース。NNのパラメータは、NNが予測したノイズとベイズの定理によって計算されるノイズの理論的な推定値のMSE誤差が最小となるように誤差逆伝播法によって学習する。
Unetを繰り返し（典型的には1000回）伝搬させるので、生成速度は他の手法と比較するととても遅い。

研究分野における位置付け

• GAN: 安定した学習が難しい。生成されるデータの多様性が限定的。潜在変数と生成されたデータは明示的な関わりを持たない。
• VAE: 代理損失(negative ELBO loss)による最適化。
• Flow-based models: 変換を可逆にするためにアーキテクチャに強い制約を課す
• 拡散モデル: 伝搬する情報は入力データと同じ次元をもつ。生成されるデータの精度は高いが、生成速度がとても遅い（GANの数千倍遅い。生成を高速化するテクニックを使っても数十倍〜数百倍程度）

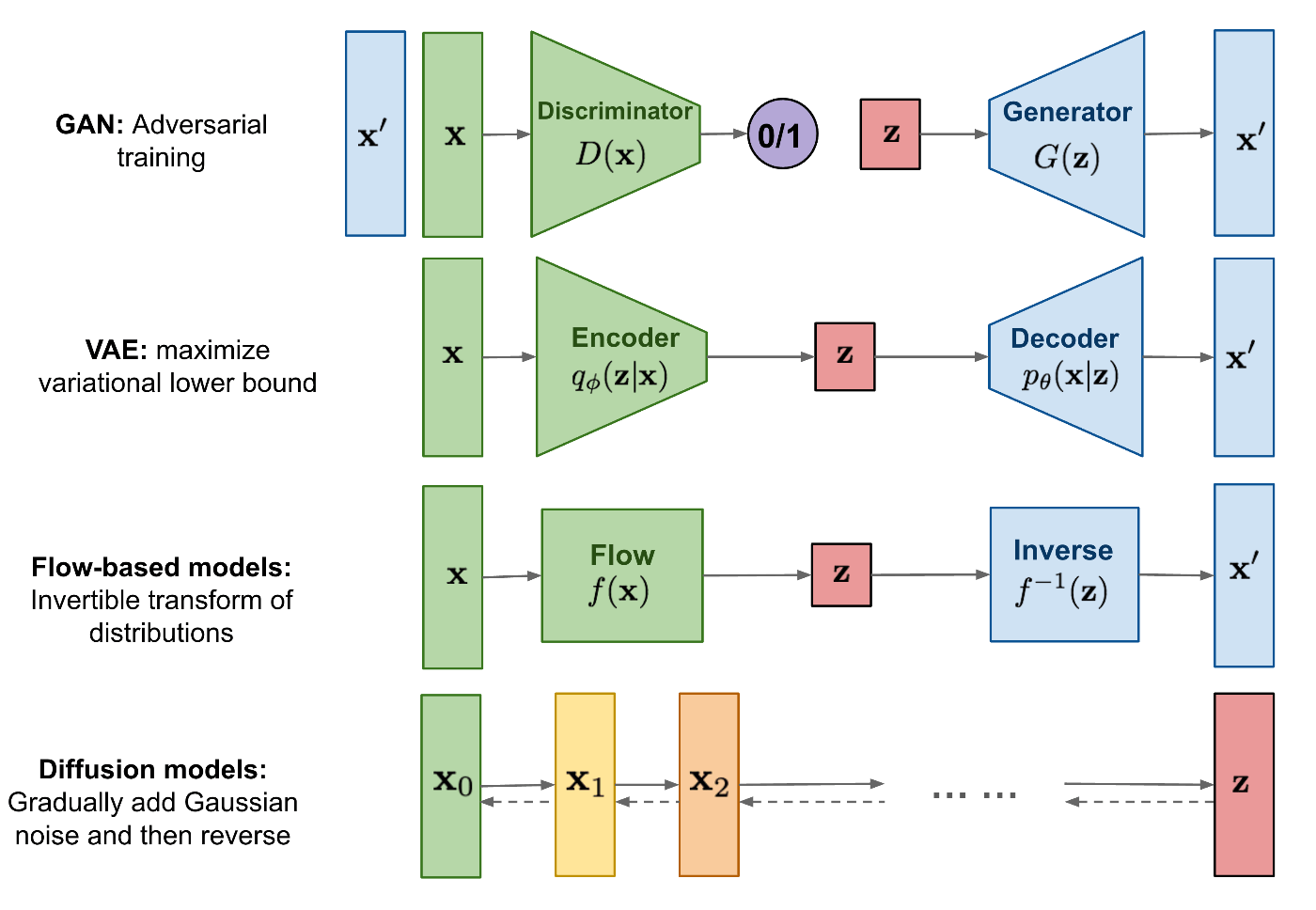
Fig. 1 各生成モデルのアーキテクチャの比較。source

メモ

Forward diffusion process

Connection with stocastic gradient Langevin dynamics

• 勾配\nabla_\mathbf{x}\log p(\mathbf{x})の情報のみを使ってパラメータを更新する手法
  
  \mathbf{x}_t=\mathbf{x}_{t-1}+\frac{\mathbf{\epsilon}}{2}\nabla_\mathbf{x}\log p(\mathbf{x}_{t-1}) + \sqrt{\mathbf{\epsilon}}\mathbf{z}_t, \text{where } \mathbf{z}_t \sim \mathcal{N}(\mathbf{0}, \mathbf{I})

所感

• 結局stochastic gradient Langevin dynamicsとどう関連しているのかがよく分からなかった。

Reverse diffusion process

• L_\mathrm{VLB}の導出過程にて、\mathbf{x}_{t-1}は\mathbf{x}_{0}から再起的に生成されるので、\mathbf{x}_{t-1}が条件変数なら\mathbf{x}_{0}も条件変数に追加して差し支えない。

Parametrization of L_t for Training Loss

• Q. 生成過程におけるノイズ項\mathbf{z}_\theta(\mathbf{x}_t, t)と\sigma_t\mathbf{z}のそれぞれの違いは？
  • \mathbf{z}_\theta(\mathbf{x}_t, t): NNが予測するノイズの効果を打ち消す項
  • \sigma_t\mathbf{z}: 生成時に明示的に付加するノイズ。パラメータ\sigma_tはDDPMでは\sigma_t=\beta_tまたは\sigma_t=\tilde{\beta_t}, DDIMでは\sigma_t=\eta \tilde{\beta_t}で与える。
    • \beta_t: ノイズスケジュールによってあらかじめ与えるパラメータ
    • \tilde{\beta_t}: ベイズの定理によって計算される、復元時のノイズの理論的な推定値。

所感

• 生成時のノイズ\sigma_tを付加するのはどういった意味があるのか？（0ではダメなのか？）ちなみに、DDIMでは\sigma_t=0の時が最も尤度が高くなっている。