Paper: Distribution-Aware Calibration for Object Detection with Noisy Bounding Boxes

概要

noizy labelに対応するために、box座標の確率的表現をモデル化し、以下の4STEPでend-to-endで学習する手法を提案した。

• STEP1. 自身が予測したproposalの分布に基づく予測確率分布のパラメータ推定
• STEP2. 予測確率モデルから新たにproposalをサンプルして分布の推定をよりロバストにする（一種の擬似ラベル）
• STEP3. 予測確率モデルに基づくGT boxの補正（一種の自己教師あり学習）
• STEP4. 確率予測分布の回帰headの追加

アーキテクチャ

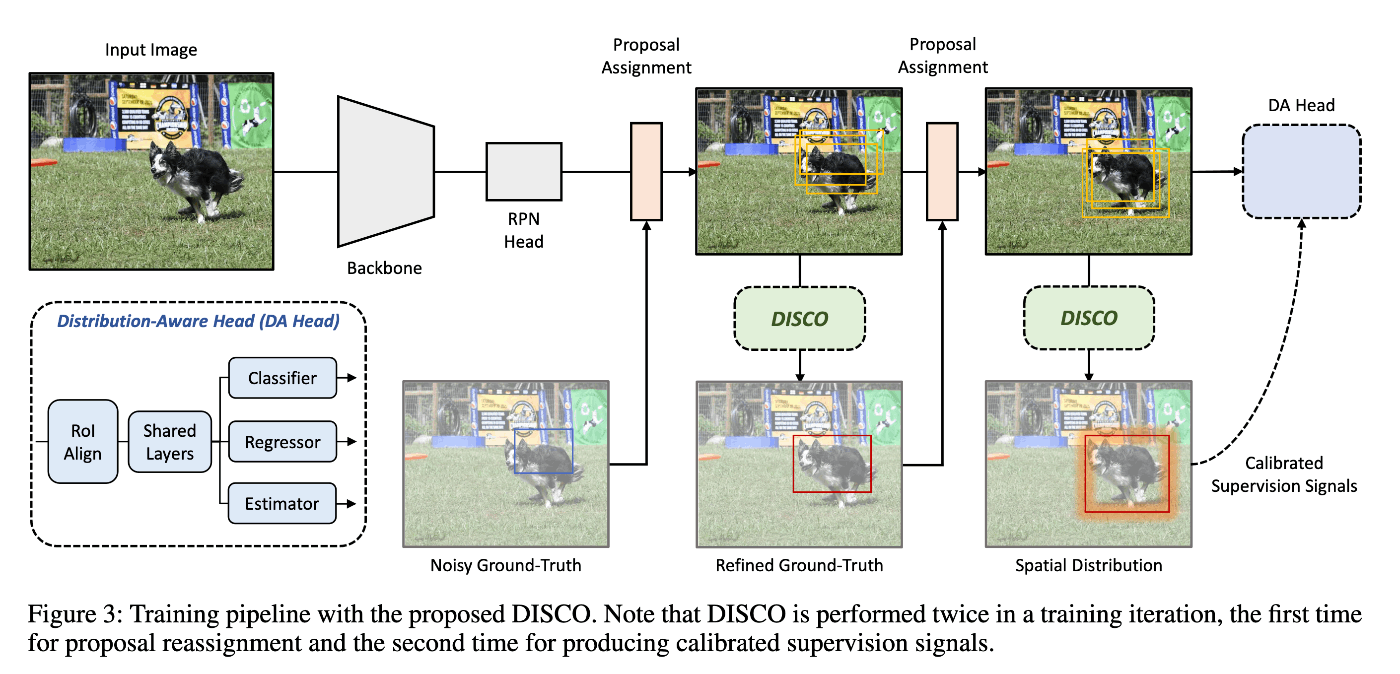
補正の概要

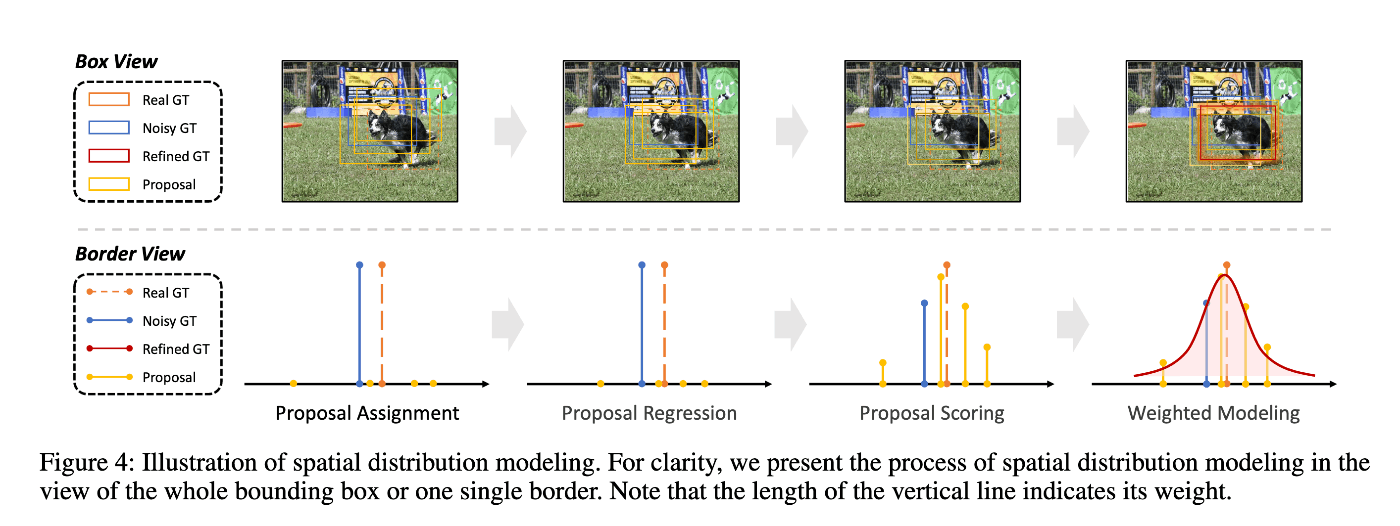
STEP1. 確率的予測に基づくbox correction

処理の流れは以下：

1. backboneのproposalからオフセットを回帰する（RoIAlign^[1]を利用）
2. proposalを回帰したオフセットの分だけtranslateして1段階目の荒いのproposalを作る
3. オフセットのずれを加味したfeature mapの領域(RoI)に基づきproposalのclassスコアを予測する
4. 3のclassスコアに基づいてGTとマッチしたproposalを重みづけ平均から平均と分散を計算する

two-stage detectorの論文はちゃんと読んでないが、1-3はおそらくR-CNNなどtwo-stageの一般的なdetectorの回帰方法に従っていると思う。
提案手法の特徴は4のステップで、GTに紐づくproposalの集合はGTの真の確率分布のサンプルになっているという暗黙の仮定に基づきパラメータの推定を行っている。なお、Gauss分布はbox座標の4つの次元でそれぞれ独立して行なっている（異なる次元同士の相互相関は考えない）。

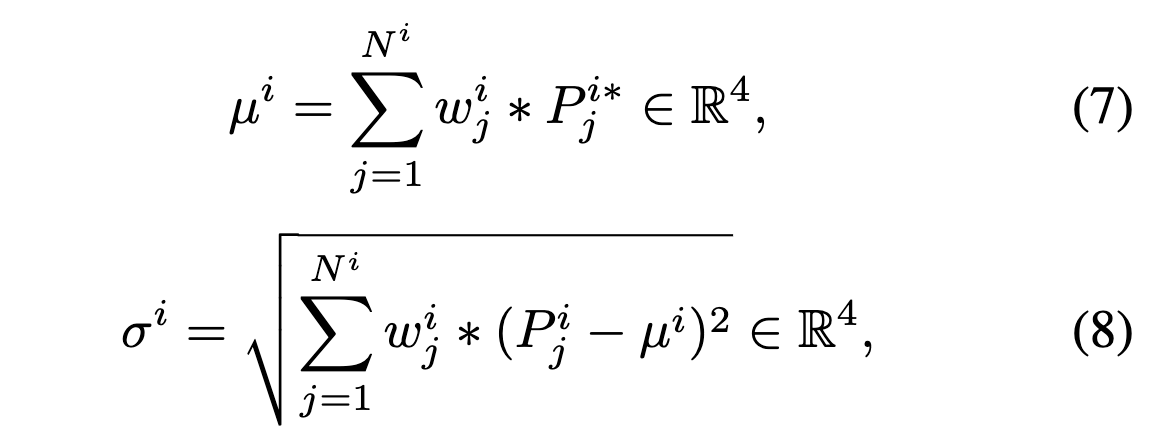
STEP2. 確率モデルからサンプルしたproposalのaugmentation

1で推定したパラメータに基づくモデルの推定確率分布からサンプルして新たにproposalを生成する(augmented proposals)。
1つのGTとマッチしたproposalの集合 (N^i 個)に対して、N^\prime 個生成する（N^\prime はハイパーパラメータ）。

元のproposalとaugmented proposalを合わせたproposalの集合から、class予測値が最大となるproposalを各GTに対して求め、それらのclass確率が最大となるようにcross entropy損失により最適化する。なお、confidenceが最大のboxのみでlossを計算しているので、このlossについてはTop-1 proposalのclass予測値のみを対象にして最適化している。

この追加のlossは提案手法の本質からするとoptionalだと思うが、ablation studyの結果によるとこの追加のlossを追加することでAP^{50} で9.0ポイントの影響があり、モデルの学習効率の改善に少なからず寄与をしたことを示している。

STEP3. 確率モデルに基づくGT boxのcorrection

STEP1で計算したbox座標の平均 \mu_i とnoizyなGT box座標を重みづけ平均によって補正する。

推定値の重みは学習の初期段階では信頼できないので、ハイパーパラメータ \beta によりcapする（実験では \beta=0.8 を使用）。

ablation studyの結果ではこの手法の追加でAP^{50} で+16.8ポイントの改善を報告しており、この部分が提案手法の性能改善の主力要因であることがわかる。

STEP4. 確率予測分布の回帰headの追加

提案手法は予測確率分布を自身が予測したproposalのサンプル統計値から推定することができるが、既存手法のように、Gauss分布の標準偏差\sigma_i をfeature mapから暗黙的に回帰するheadを追加することでさらに学習効率が良くなるという結果を示している。ablation studyの結果によれば、追加headによる回帰lossを追加することでAP^{50} で1.8ポイントの影響があったを報告している。

結果

VOC/MS COCOデータセットに人工的にnoiseを加えて生成したデータセットに対して既存手法と提案手法の性能を比較した。

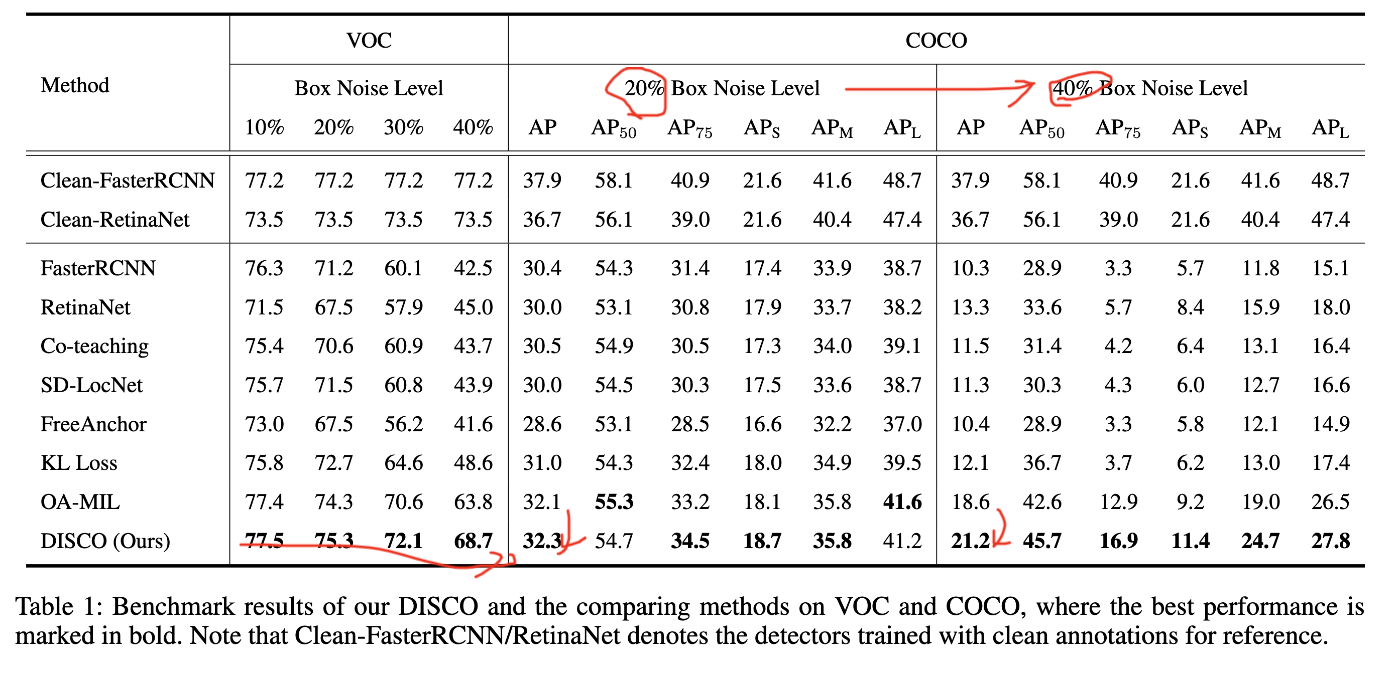
noiseが小さい場合は既存手法とtieだが、noiseが大きくなるにつれて提案手法が既存手法を大きく上回る性能を示した。
つまり、ラベルのnoiseの大きい場合に提案手法は特に有効であることを示している。

Ablation Study

表VOCに40%のnoise levelを付加したデータセットに対するAP^{50} の結果を示している。

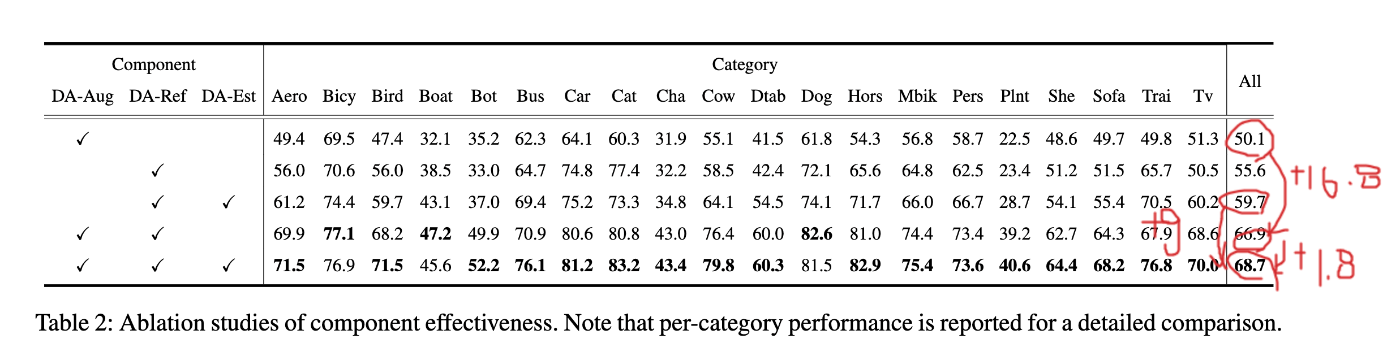
個人的な評価

確率分布を仮定してboxの座標を推定する既存手法には、以下のものがある。

1. パラメータ固定の分布に対して確率分布を回帰する: GTを標準偏差\sigma のgauss分布と仮定して、そのsoftlabelに対して確率分布を回帰する。\sigma はハイパーパラメータとして固定のものを用いる（例: 一般的なheatmap回帰）。
2. 分布のパラメータを何らかの方法で推定する: 例: 分布のパラメータを回帰するheadを用意して、パラメータに基づいて生成した予測分布とone-hotラベルとのKL divergenceを目的関数として回帰する。

本手法は2に属するもので、\sigma をfeature mapからback box的にに回帰するのではなく、モデルが推定したproposal boxのサンプル分布を用いて直接推定するアプローチを用いる。

所感

end-to-endな自己教師あり手法の一つとして、モデル設計の参考になった。
ただ、ノイズを人工的に埋め込んだsynthesizedデータセットで評価したのみなので、人間のラベラーが作り込んだartifactに対しても有効なのかが気になる（ガウス分布で生成したノイズをガウス分布で推定するのはかなり問題を緩和しているように思える）。
あと、特にコンペなどを想定した場合、評価setもnoisyな場合は補正すると逆にスコアが悪化したりすることも考えられるので、効果については結局実際に適用してみないと分からないな、という感じ。