Linear Transformerの近況

Summary

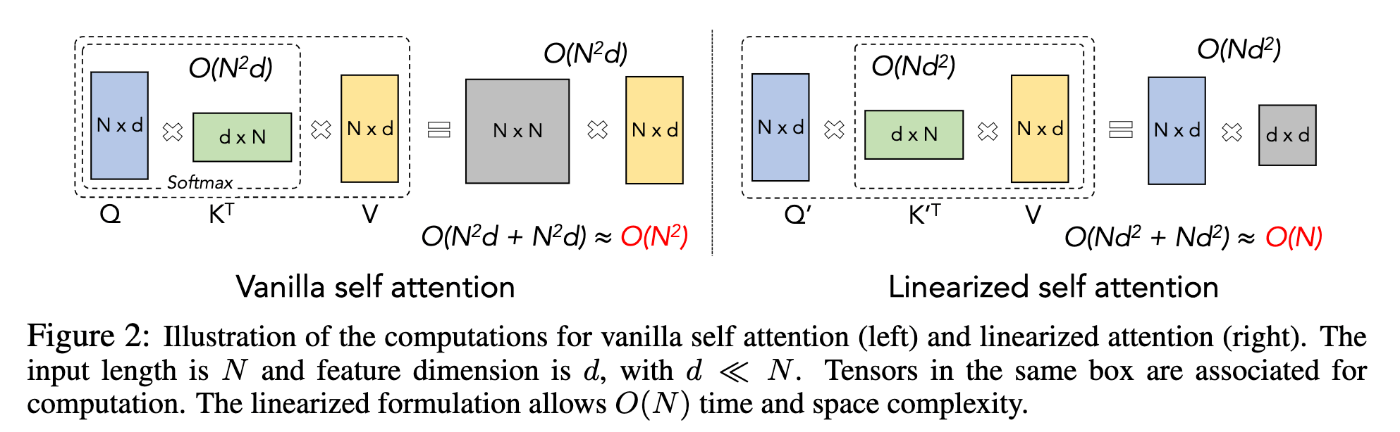
普通のtransformerのsoftmax attentionはトークン長の2乗に比例した計算量がかかるが、トークン長の線形の計算量で実現できる代替アーキテクチャについての一連の研究（しばしばlinear transformerと言及される）がある。具体的にはsoftmax attentionを代替の演算で置き換え、QKよりも先にKVを計算できるようにすることで線形計算量を実現する手法が一般的に用いられる。
最近ではKernel法（後述）との関連から理論的にsoftmax attentionを近似する処理を導出する手法[3,4]も提案されている。

Kernel法について

Kernel (Function)とはベクトルの類似度ののようなもので以下のようなベクトルからスカラーへの射影として定義される。

Kernel関数の値は、Kernel Trickと呼ばれる定理により、入力ベクトルにある射影を適用した時の内積と等しいことが知られている。

内積で計算できることのメリットは、計算順序を入れ替えることができるようになること。例えば、softmax attentionは \mathrm{softmax} (QK^\top) V の形式だが、softmaxが非線形演算なのでQKを先に計算する必要がある。しかし、softmaxが \phi(Q)\phi(K^\top) の形式に分解できたとすると \phi(K^\top)V の部分を先に計算することで計算量を O(N^2D) から O(ND^2) に削減できる（ N \gg D と仮定）。この手法は線形計算量を実現するための一般的な手法のようである（e.g. Performer[5], RetNet[6]）。

cosFormer[4]

• softmax attentionをKernel法の枠組みで解釈できることを示した先駆的研究。
• 提案手法はsoftmaxの代わりの演算として、ReLUとcosine weightningを提案する。

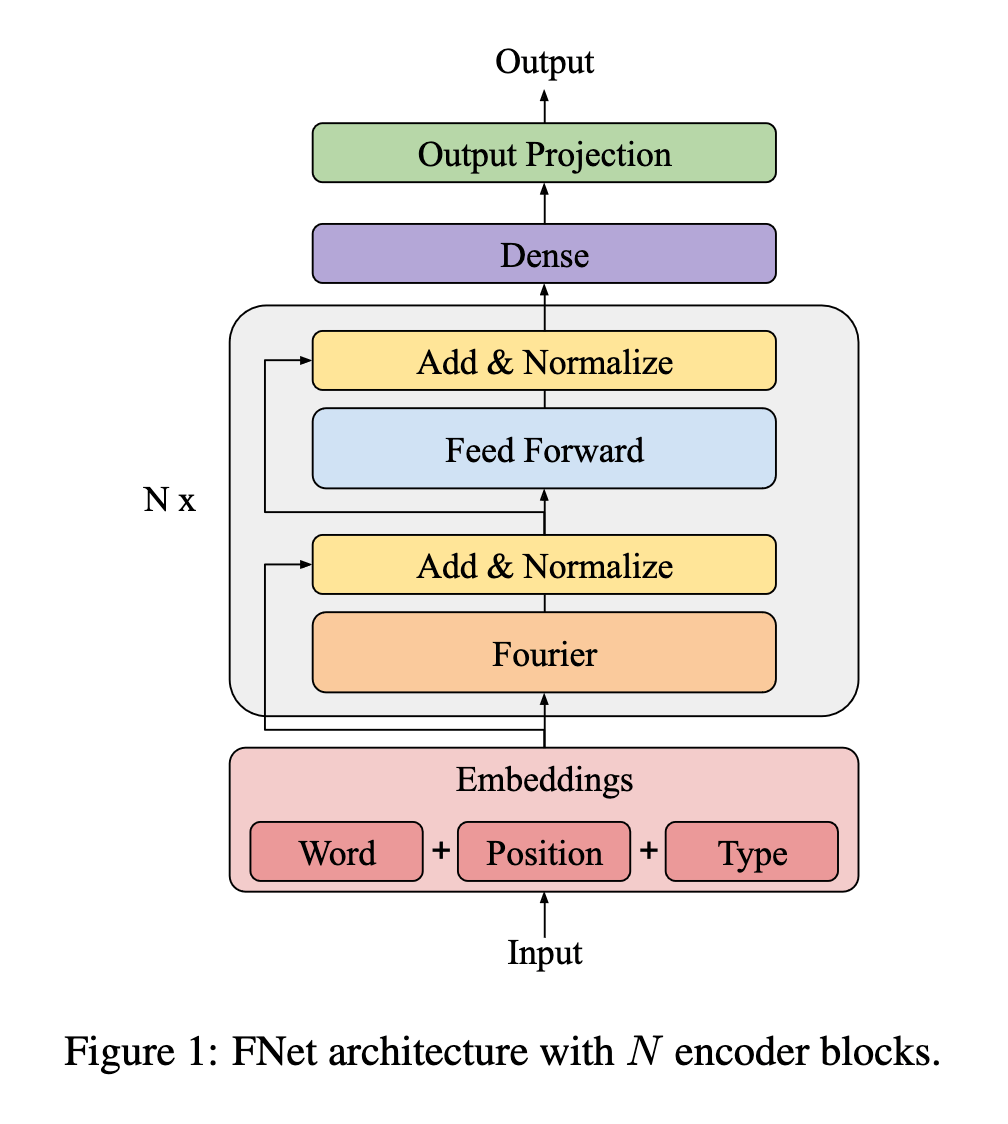
FNet [2]

• Softmax attentionの代替としてDFTを採用
  

DCFormer[1]

• Softmax attentionの代替としてDCTを採用

DiJiang[3]

• Kernel法における射影関数として、DCTを採用。softmax attentionと定数倍を除いて等価となることを数学的に証明した。
• 既存のsoftmax attentionで計算したattentionを流用し、定数倍の部分のみ学習可能なパラメータとして再学習する

Reference

1. Discrete Cosin TransFormer: Image Modeling From Frequency Domain
2. FNet: Mixing Tokens with Fourier Transforms
3. DiJiang: Efficient Large Language Models through Compact Kernelization
4. cosFormer: Rethinking Softmax in Attention
5. Rethinking attention with performers
6. Retentive Network: A Successor to Transformer for Large Language Models

Kernel法で定式化することで、Softmax attentionを含む各種attentionを統一的に解釈可能であることを示した先駆的研究(preprintの日付は2019年)。

この論文の結論は

1. 異なるKernelの設計Exponential kernel or RBF(Gaussian) kernelが良かった。linear kernelは収束せず（正定値性の条件を満たさないため？）
2. Positional Embeddingの設計 -> 加法的f(x_q + t_q, x_k + t_k) or 乗法的f_x(x_q, x_k) * f_t(t_q, t_k)が良かった
3. maskが設定してある場合は順序普遍性は成り立たなくなるが、それでもPEを与えることによりゲインが得られた
4. ValueにPEを加えてもゲインは得られなかった

所見

• 他の論文で明に議論されていないmaskの問題についても定式化されている。
• (QxK)xV->Qx(KxV)と順序変更することで計算コストが削減できる点については触れられていない。
• 実装が公開されていないので不明だが、kernelは正規化しないと学習が不安定なのでは？

Reference

• (再掲) Transformer Dissection: A Unified Understanding of Transformer's Attention via the Lens of Kernel