Zenn
🐕

TAID: 学習の進捗状況に応じたAdaptiveな蒸留手法

2025/02/18に公開
bilzardpaper
knowledgedistillat
tech

この記事は以下の論文をまとめたものです。論文で直接触れられていない以下の内容についてはbilzardが独自に行なった考察に基づいています。

  • 内挿系数の更新の数値シミュレーション(Appendix B-1)
  • 内挿系数の更新式の意味について(Appendix B-2, B-3)

paper: TAID: Temporally Adaptive Interpolated Distillation for Efficient Knowledge Transfer in Language Models, Feb 2025

https://arxiv.org/abs/2501.16937

Summary

  • 機械学習モデルを知識蒸留(Knowledge Distillation)する場合、モデルサイズのギャップが大きいと蒸留タスクが難しいことが経験的に知られている
  • このような設定では1) モード崩壊(mode collapse) 2) モード平均化(mode average) の両極端の局所解に陥るリスクがある。
  • 上記のような背景のもと、本論文ではモデル間のサイズギャップが大きい設定で安定して学習する蒸留手法を提案する。
  • 具体的には、生徒の自己蒸留ラベルと教師の蒸留ラベルとの間で内挿を行い、学習の進行に伴い生徒ラベルから教師ラベルへと向かうスムーズな移行を実現する。
  • 本論文の蒸留手法を使ってスマートフォンで動作するモデルTinySwallow-1.5Bをリリースした(Appendix A 参照)

背景

モード平均化とモード崩壊

単純なモデルで複雑なモデルを近似しようとすると、以下のいずれかの両極端の局所解に収束するリスクがある[2]。

  • モード平均化(mode-averaging): 分布の全体をカバーしようとして過剰に滑らかな解に収束する。
  • モード崩壊(mode-collapting): 最も確率密度の高い領域の特徴のみを捉えて他の特徴を無視する。

例: 3峰のデータ分布を1峰のガウス分布で近似する場合:


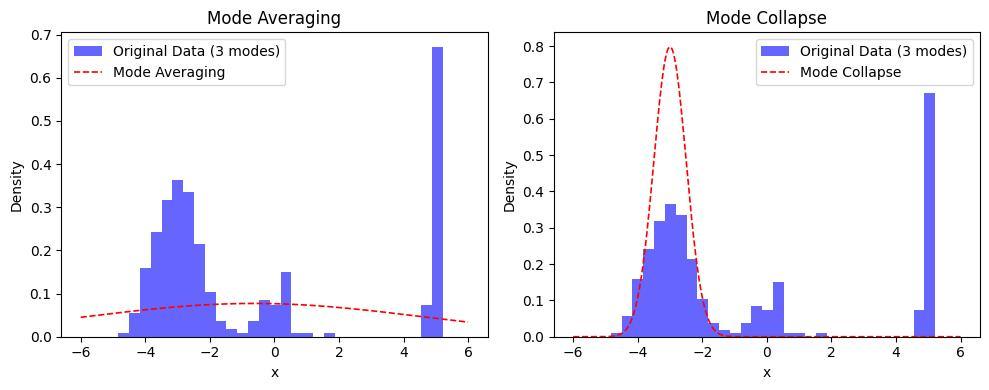
(source: bilzard)

手法

蒸留ラベルのスケジューリング

  • アイデア: （特に学習の初期段階の）生徒モデルにとって教師モデルの複雑な分布の特徴を捉えるのが難しいのだとすると、両者中間の分布なら適合しやすいのでは？
  • 解決方法: 蒸留ラベルをなだらかに生徒から教師に移行する。具体的には、生徒ラベル(self-distillation)と教師ラベルを内挿系数 t で線形補完し、内挿系数を学習の進行状況とともに増やしていく。

補完系数のスケジューリング方法

  1. step数の関数 (static)
  2. 目的関数と連動させる (adaptive) -> Temporaly Adaptive Interporated Distillation (TAID)

TAID: 学習の進捗に応じて内挿系数をスケジューリングする

  • 目的関数は(2)式のようなKL-divergence lossだが、蒸留ラベルとして(1)式のように教師ラベル p と自己蒸留ラベル q _ \theta の間を内挿系数 t で内挿する
  • 学習の進捗度 \delta _ n は 直前のステップと比較してどのくらいlossが低下したか？ で判定する
\delta _ n = \frac{J ^ {(t-1)} _ \text{TAID} - J ^ {(t)} _ \text{TAID}}{J ^ {(t-1)} _ \text{TAID} + \epsilon}
  • 学習の進捗度 \delta _ n を元に、内挿系数の変化率 \Delta t を決める。進捗度が早いとペースを早め、遅いと緩める
  • 基本的なアイデアは以上だが、学習を安定化するために以下を入れている
    1. バッチごとのばらつきを軽減するため進捗度のモーメント (m _ n)を取る
    2. 内挿パラメータの下限(t _ \text{linear})を設定し、学習が一定以上のペースで進行するのを保証する
  • t _ {n+1} の更新式はnが増加するにつれ、指数関数的に1に収束する形式になっている(Appendix B-2参照)。\alpha, \sigma = \text{sigmoid}(m _ n) はともに収束速度を調整するパラメータである。




(source: TAID: Temporally Adaptive Interpolated Distillation for Efficient Knowledge Transfer in Language Models[1])

結果

  • 掲載は省略するが、論文では各種下流タスクでの比較で既存手法との優位性を報告している
  • Figure2左: TAIDによる内挿係数 t のstepごとの変化を表す→ \alpha の増加とともに内挿系数が急激に増加する（内挿系数のシミュレーション結果はAppendix B-1参照）
  • Figure2中央: 提案手法のstepごとのlossの推移を表す。ナイーブなKL-div関数と比較すると、lossの値が学習を通じて概ね一定になっている→生徒モデルにとって無理のない教師信号を送れている
  • Figure2右: 教師モデルのサイズをスケールした時の生徒モデルの学習結果への影響。KLは2.8Bで性能が落ち込んでいて不安定だが、TAIDはモデルのパラメータ数とともにスケールしている→学習がより安定している


(source: TAID: Temporally Adaptive Interpolated Distillation for Efficient Knowledge Transfer in Language Models[1])

所感

  • 学習状況をモニタリングしながらadaptiveにパラメータをスケジュールさせる事例として参考になった
  • これがうまくいく理由（背後のメカニズム）が何なのかはよくわからなかった。
  • 蒸留に限らず、教師あり学習でも本手法は有効だろうか？

Reference

Appendix

A. TinySwallow-1.5B

本手法を使ってスマートフォンで動作可能な軽量の蒸留モデルTinySwallow-1.5Bがリリースされている（iPhone14で動作確認ずみらしい）。

  1. TinySwallow-1.5B[4a]: Qwen2.5をベースに日本語のテキストを使って蒸留した。
    • teacher: Qwen2.5-32B-Instruct
    • student: Qwen2.5-1.5B-Instruct
  2. TinySwallow-1.5B-Instruct[4b]: TinySwallow-1.5Bを日本語のInstruction Tuningしたもの。
    • Training Datasets:
      • Gemma-2-LMSYS-Chat-1M-Synth
      • tokyotech-llm/swallow-magpie-ultra-v0.1
      • tokyotech-llm/swallow-gemma-magpie-v0.1

ベンチマーク結果:


(source: 新手法「TAID」を用いた小規模日本語言語モデル「TinySwallow-1.5B」の公開[3])

B. 内挿系数の動力学

B-1. 数値シミュレーション

論文のFigure 2左を数値計算により再現する。

シミュレーションの仮定: \text{sigmoid}(m _ n) = \sigma で固定とする

→ \sigma=1 はモデルが最大限にaggressiveな回帰をした場合の内挿系数のスケジュールを表す。
実際は \text{sigmoid}(m _ n) は学習の進捗に応じて0から1までの値をとるので、t _ n は図の曲線と線形スケジュールの間にある単調増加な曲線を描く。



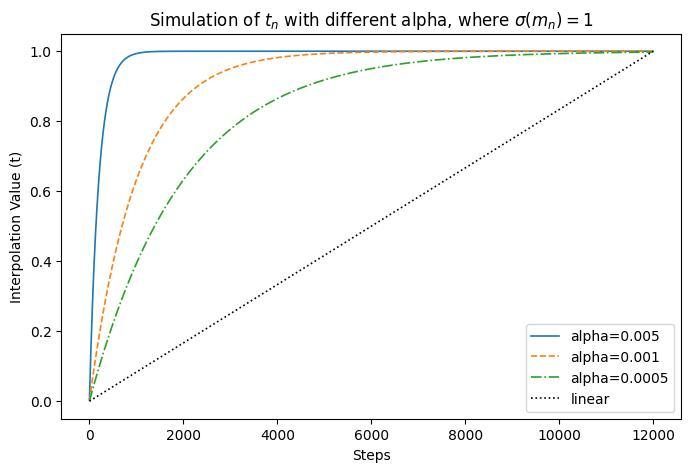
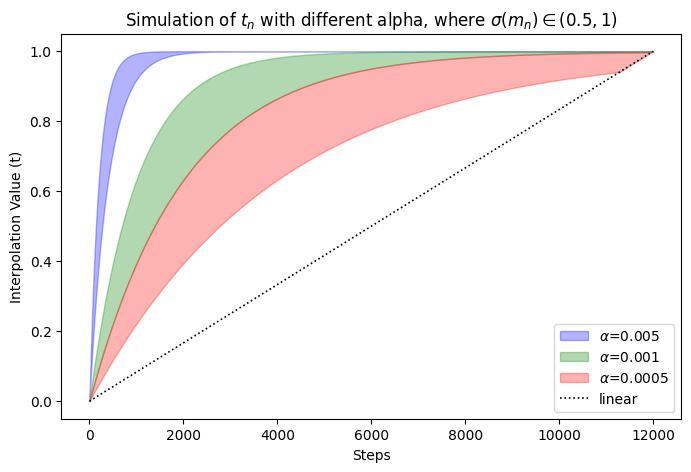
(source: bilzard)

ソースコード:

def calc_next(t_n, step, alpha=5e-3, sigma=1, t_end=1, T=12000):
    t_linear = step / T
    return min(t_end, max(t_linear, t_n + alpha * sigma * (1 - t_n)))


def simulate(t_init=0, T=12000, **kwargs):
    data = []
    t = t_init
    for step in range(0, T):
        t = calc_next(t, step=step, T=T, **kwargs)
        data.append(t)
    return data


_, ax = plt.subplots(figsize=(8, 5))
x = np.arange(0, 12000)
s1, s2 = 0.5, 1
for alpha, s, c in zip([5e-3, 1e-3, 5e-4], ["-", "-", "-"], ["blue", "green", "red"]):
    d1 = simulate(alpha=alpha, sigma=s1)
    d2 = simulate(alpha=alpha, sigma=s2)
    ax.fill_between(x, d1, d2, label=f"$\\alpha$={alpha}", linestyle=s, color=c, alpha=0.3)

ax.plot(np.linspace(0, 1, 12000, endpoint=False), "k:", label="linear")
ax.legend()
ax.set(
    xlabel="Steps",
    ylabel="Interpolation Value (t)",
    title=f"Simulation of $t_n$ with different alpha, where $\\sigma(m_n)\\in({s1}, {s2})$",
)
plt.show()

B-2. 解析的な解

なお、\sigma が定数の場合は数値シミュレーションをしなくても差分方程式を解くことで解析的に求められる。
t _ {n+1} の更新式でmin/maxの条件を取り払って単純化すると、

t _ {n+1} = t _ n + \alpha \cdot \sigma (1 - t _ n) \tag{B1}

と表される。これを n について解くと、a = \alpha \cdot \sigmaを用いて

t _ n = (1 - a)^n (t _ 0 - 1) + a \tag{B2}

を得る。これはステップ数nを増加するにつれて指数関数的に1に収束する形式になっている。

B-3. グラフによる別解

以下では(B-1)のグラフによる別解を示す。(B1)により

t _ {n+1} = (1 - a) t _ n + a \tag{B3}

である。このことから、(x, y) = (t _ n, t _ {n+1}) を2次元グラフにプロットすると、(B3)で表される直線上にある。
従って、初期値 t _ 0 = 0 を開始点とし、 t _ {n+1} を順次更新していくと、点 (t _ n, t _ {n+1}) は下図の赤い点線を経由しながら点 (1, 1) へと収束していく。

a = \alpha \cdot \sigma は収束の速さを調整するパラメータであり、\alpha および \sigma を大きくすると収束が加速される。


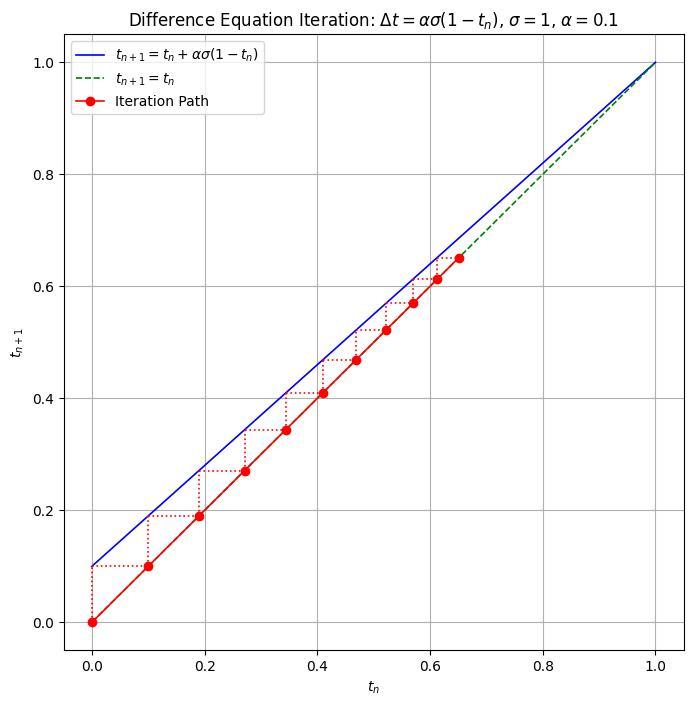
(source: bilzard)

GitHubで編集を提案

Discussion