Zenn
📌

Superlets: 時間-周波数解析における「超解像度」filterbank

2024/04/17に公開
#
stft
#
cwt
#
spectrogram
tech

概要

KaggleのHMSコンペ[4]の1st place solution[3]のアンサンブルモデルの一つにSuperlets[1]というfilterbankが使われていた。このfilterbankの特徴を原著により確認していく。

原著ではEEGに対する視覚的評価などを行なっているが、ここではとりあえず何をやっているかを把握したいだけなので理論的な内容に留める。

なお、タイトルの「超解像度」というのは原著のタイトルにちなんだ。おそらく著者らの意図としては「単一フィルタにおける理論的な制約を超えた解像度の表現が得られる」というのが言いたいのだと思われる。

用語

日本語でどう訳すのが一般的かわからなかったが、本稿では仮に以下の訳を用いる。

  • 周期数(number of cycles): Wavelet変換(Morlet)における窓関数のパラメータc。直感的には「window中に含まれる有効な周期の数」とみなすことができる。
  • 中心周波数(center frequency): Fourier/Wavelet変換における基底関数のパラメータf。直感的にはフィルタにより抽出される周波数の主要な成分とみなすことができる。spectrogram/scalogramにおけるY座標に対応する。
\Psi_{f,c}(t) = \frac{1}{B_c\sqrt{2\pi}} e^{\frac{-t^2}{2B_c^2}}e^{j2\pi ft} \tag{1}
B_c = \frac{c}{k_\text{sd}f}
  • k_\text{sd}: Wavelet変換（Morlet）のガウス窓関数におけるハイパーパラメータの一つ。直感的には標準偏差の何倍までの区間を有効とみなすか？に相当する。

機械学習(ML)技術者向けの補足

基本的にはFourier変換もWavelet変換も畳み込み演算の1つとみなすことができる（実際にそうやって実装できる）。機械学習における畳み込みフィルタの形状は学習可能だが、Fourier変換やWavelet変換ではある数式によって計算される固定の形状を持つ。

Waveletの一種であるMorletでは、フィルタの形状は式1によって計算される。主要な項は2つあり、窓関数と基底関数からなる。「原信号から特定の周波数成分を抽出する」という目的に必要なのは基底関数のみだが、時間周波数解析では「特定の時点における周波数成分の構成」が知りたいので、原信号の特定の時間領域を切り出す目的で窓関数が導入された。

窓関数は矩形の窓が直感的に理解しやすいが、矩形窓だと本来欲しい中心周波数以外の余計な周波数成分がたくさん抽出されるので実用ではあまり使われない。いい感じの窓関数がいくつか提案されたが、Morletではガウス関数が採用されている。

窓関数は一般的には時間とともになだらかに減衰するため、上で記述した「周期数」の直感的説明は非常に曖昧である。つまり、「窓関数中のk \sigmaまでにいくつの波の周期が含まれるか？」といった雑な指標を指しているに過ぎない。

Fourier変換とWavelet変換の違いについて

まず、Fourier変換とWavelet変換の違いについて確認する。

  • Fourier変換: 窓関数の時間幅が固定。周期数は中心周波数に比例する(Fig.1-a)。
  • Wavelet変換: 周期数が固定。一方で窓関数の時間幅は中心周波数に反比例する(Fig.1-b)

両者に共通する特徴として、理論的な制約(Heisenberg–Gaborの不確定性原理[2])により周波数領域の解像度と時間領域の解像度がトレードオフの関係にある。つまり、両方の特徴をバランスよく抽出したい場合、最適なフィルタのパラメータをデータに合わせてチューニングする必要がある。

また、Wavelet変換では中心周波数ごとに解像度が一定でないという特徴がある。これは周波数のシフトに対して出力スペクトルの表現が変わってしまうことを意味するので、周波数のシフトに対して不変な表現を捉えたい場合は不都合な制約と言える。

注）HMSコンペでは異なるパラメータのSTFTのスペクトログラムを入力とするモデルのアンサンブルが効果的だった。おそらく捉えたい特徴によって最適なフィルターのパラメータが異なるためではないかと思われる。

Superlets

上記の事情より、STFT/CWTの単一のfilterで時間領域と周波数領域の特徴を同時に解像度高く捉えることは理論的な制約により難しい。そこで、論文[1]では単一filterでなく、複数の周期数の異なるfilter(wavelet)を合成することを提案する(Fig.1-c)。つまり、Superlets(SLs)は波の周期数の異なる複数のwaveletの集合からなる。

SL_{f, o} = \left\{ \Psi_{f,c} | c = c_1, c_2, \ldots, c_o \right\}

i番目の周期数c_iは最小の周期数c_1の倍数となるようにとる。oはSuperletsに含まれるwaveletの数であり、階数（order）と呼ぶ。

Sperletsのspectrogram上での表現は、個々のwaveletの周波数応答の幾何平均で定義される。

R\left[SL_{f, o}\right] = \sqrt[o]{\prod_{i=1}^{o} R \left[\Psi_{f, c_i}\right]}

注) 平均でなく幾何平均を採用した理由は、異なる周期数のwaveletで共通する特徴を強調したいためだと思われる。つまり、周波数方向か時間方向にぼやけた周波数応答の影響が小さくなるように設計されているのだと思われる。

Adaptive Superlets

WaveletはSpectrogram上における中心周波数が低い領域ほど解像度が高いという特徴を持つ(Fig1-b)。
つまり、低周波数の領域ではSuperletsに含まれるwaveletsの数は1つで十分であるのに対し、高周波数の領域では局所的な情報を捉えるために多くのwaveletsを必要とする。

従って、Superletsに含まれるwaveletの数を中心周波数に比例して大きくとることで中心周波数によらない一様な解像度の表現を得られることが期待できる。

[1]ではorderの最小値と最大値のみハイパーパラメータとして持ち、中心周波数の値によって線形補間によりadaptiveにsuperletsのorderを計算する方法を提案している(ASLT; Adaptive SLT)。

a(f) = o_{\text{min}} + \left(o_{\text{max}} - o_{\text{min}}\right) \cdot \left[\frac{f - f_{\text{min}}}{f_{\text{max}} - f_{\text{min}}}\right]

視覚的評価

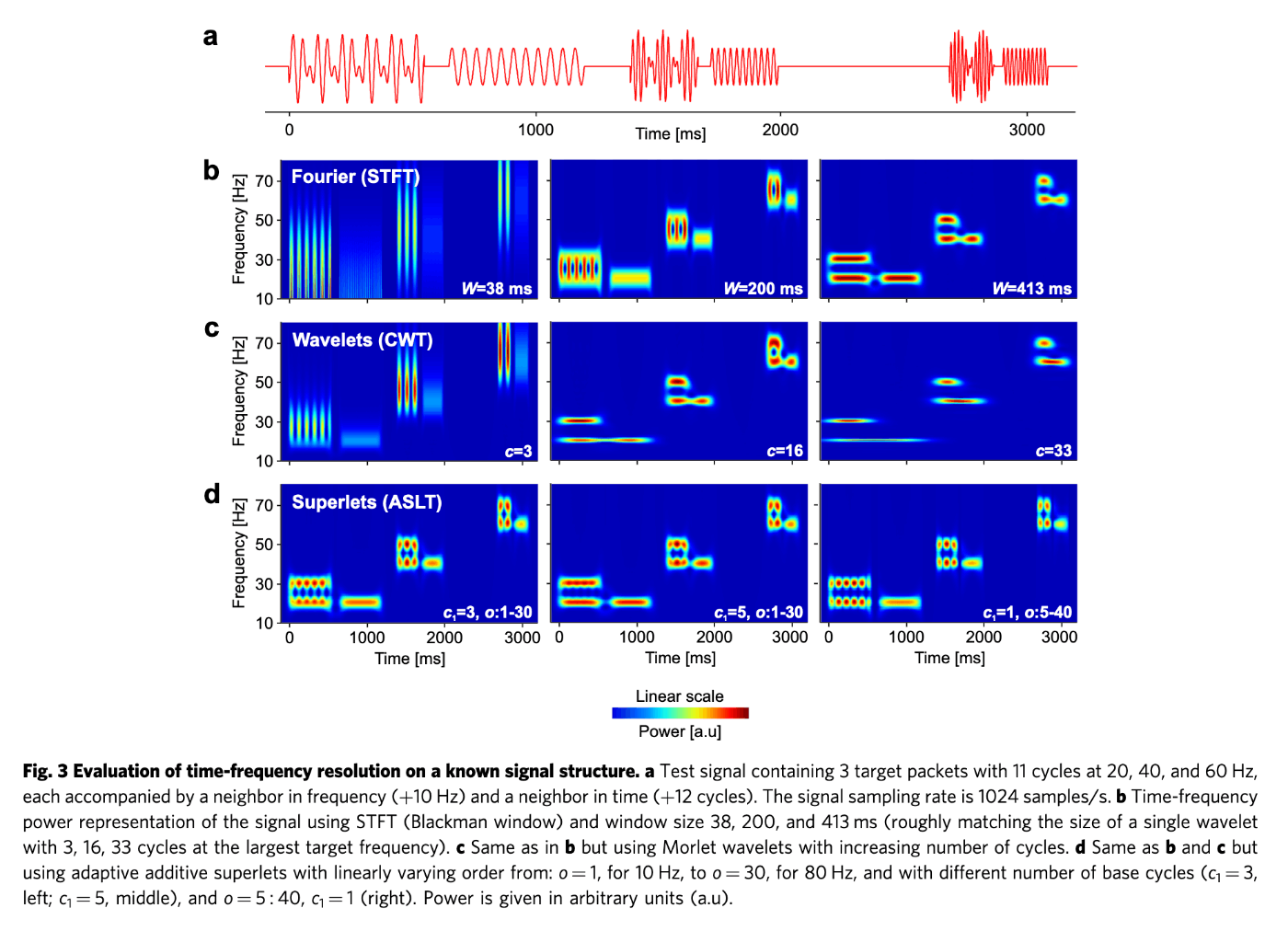
サンプル波形に対するFourier(STFT), Wavelet(CWT), Superlets(ASLT)の可視化結果をFig.3に示す。
これを見ると、STFTやCWTではfilterのパラメータが悪いと周波数領域か時間領域の解像度がぼやけているのに対し(Fig.3-b,c)、Superletsでは幅広いフィルターのパラメータに対して局所的な特徴がぼやけずに表現されていることが確認できる(Fig.3-d)。

まとめ

  • Superletsは1つの中心周波数に対して異なる周期数のWaveletを組み合わせることで、中心周波数ごとの解像度の差異を緩和することを目指した。
  • Superletsはfilterのパラメータによらずさまざまな周波数の信号に対して局所性を失わずに（像がぼやけずに）信号の特徴を捉えていることが視覚的評価により確認できた。

所感

  • Superletsは周波数のシフトに対して不変な特徴を捉えたい場合に適した手法と言える
  • filterのパラメータをチューニングしなくてもいい感じの像が得られるのは魅力的。
  • Superletsは、STFTやCWTにおいて異なるfilterのパラメータを入力としたモデルのアンサンブルを作るのと同等以上の結果になると思われる。たくさんモデルを学習しなくても同等以上の結果が得られるならこちらの方がお得（やってみないとだが）。

Reference

GitHubで編集を提案

Discussion