Object Detectionタスクにおけるpost-processing手法について

概要

Object Detectionタスクにおけるpost-processing手法について、最近読んだ論文の内容に基づいて以下の内容を解説する。

1. GT boxが混み合った状況でシーンにおけるGTラベルの混雑度(density)をモデル化してそれに基づいて事後処理におけるIoU thresholdを動的に決定する手法[1]
2. 提案boxのまとまりをよくするための補助的な損失関数を導入する手法[5]
3. 一貫性のないboxラベルの悪影響を抑制するために、boxのuncertaintyを確率的にモデル化して回帰する方法、および学習したuncertaintyを事後処理におけるboxの精度の評価値の計算に利用する手法[2]

Adaptive NMS

GT boxが混み合った領域で適切にFPを間引く

[1]はPedestrian Detection（歩行者検出）タスクに特化したNMS(Non-Maximum Suppression)アルゴリズムのバリエーションを提案した。
pedestrian detection(PD)タスクは、公共のシーンの画像から歩行者の存在するbox領域を検出するタスクで、一般的なobject detection(OD)タスクに比べて、targetの重なりが多いことが特徴である。

NMSでは固定のIoU thresholdによってmaximum confident box(以降 MCB と呼称)周辺周囲の間引くかどうかを決定するが、
PDタスクでこのようなルールベースを用いると、群集が多く重なり合っているシーンでは本来正解とするべき提案boxも間引いてしまうという問題がある。

これに対し、[1]はanchor周辺のシーンのGT boxの density(=混雑度) を推定するheadを新たに学習し、boxのconfidenceと合わせて、混雑度に応じて動的にIoU thresholdを決定する手法を提案する。

具体的には以下のようにして動的にIoU thresholdを決定する。

$$N_\mathcal{M} := \max (N_t, d_\mathcal{M})$$

表記について、$d_\mathcal{M}$ はdensity headの予測する0から1の範囲のスコアで、大きいほど混雑していることを表す。$N_t$ はNMS同様の固定のthresholdで、ハイパーパラメータである。$\mathcal{M}$ はMCBを表す。

つまり、混雑度が閾値以下の場合は通常のNMSと同じように振る舞い、混雑度が閾値以上の場合は混雑度自体を閾値とし、間引きの度合いを混雑度に応じて緩和する。

なお、本手法はSoft-NMS[4]にも適用可能で、Soft-NMSの場合は以下のようにしてboxのスコアを更新する。

$$s_i := \begin{cases} s_i, & \text{if IoU}(\mathcal{M}, b_i) < N_\mathcal{M} \\ s_i \cdot f(\text{IoU}(\mathcal{M}, b_i)), & \text{otherwise} \end{cases}$$

表記について、$s_i$ はboxのconfidenceを表し、$f$ はboxがGTとどれだけ近いかを示す尺度である。大まかにいうと、MCBとのIoUが大きいほど小さな値となり、MCBとの重なりが大きいboxのconfidenceを下げる役割を果たす(詳細は[4]を参照)。

densityの回帰head は1) classの予測結果, 2) box座標の予測結果, 3) feature mapの3つのplaneを元にして浅いconvolutionレイヤーで回帰する構成になっている(図1)。

各GT boxごとのdensityラベルは以下のように定義する。

$$d_i := \max_{g_j \in \mathcal{G}, i \neq j} \text{IoU} (g_i, g_j)$$

表記について、$\mathcal{G}$ はGT boxの集合を表す。
すなわち、他のGT boxの重なりの最大値により定義する^[1]。

[1]によると、提案手法はdensityが小さい領域(<0.4)ではNMSと同等の性能を示し、densityが大きくなるほど提案手法が既存手法よりMiss Rate(MR; 小さいほど良い)が小さくなることを示した(図2)。

また、GT boxのocclusion(=重なり)ごとの提案手法の有効性を調査した結果によるとAdaptive-NMSと後述するAggLossという手法を共に用いてCityPersonsデータセットのReasonableカテゴリ(occlusionが35%未満のGT)の予測性能が改善したことを示しており、GT boxが混み合った状況に対して提案手法が実際に有効であったことを示している。

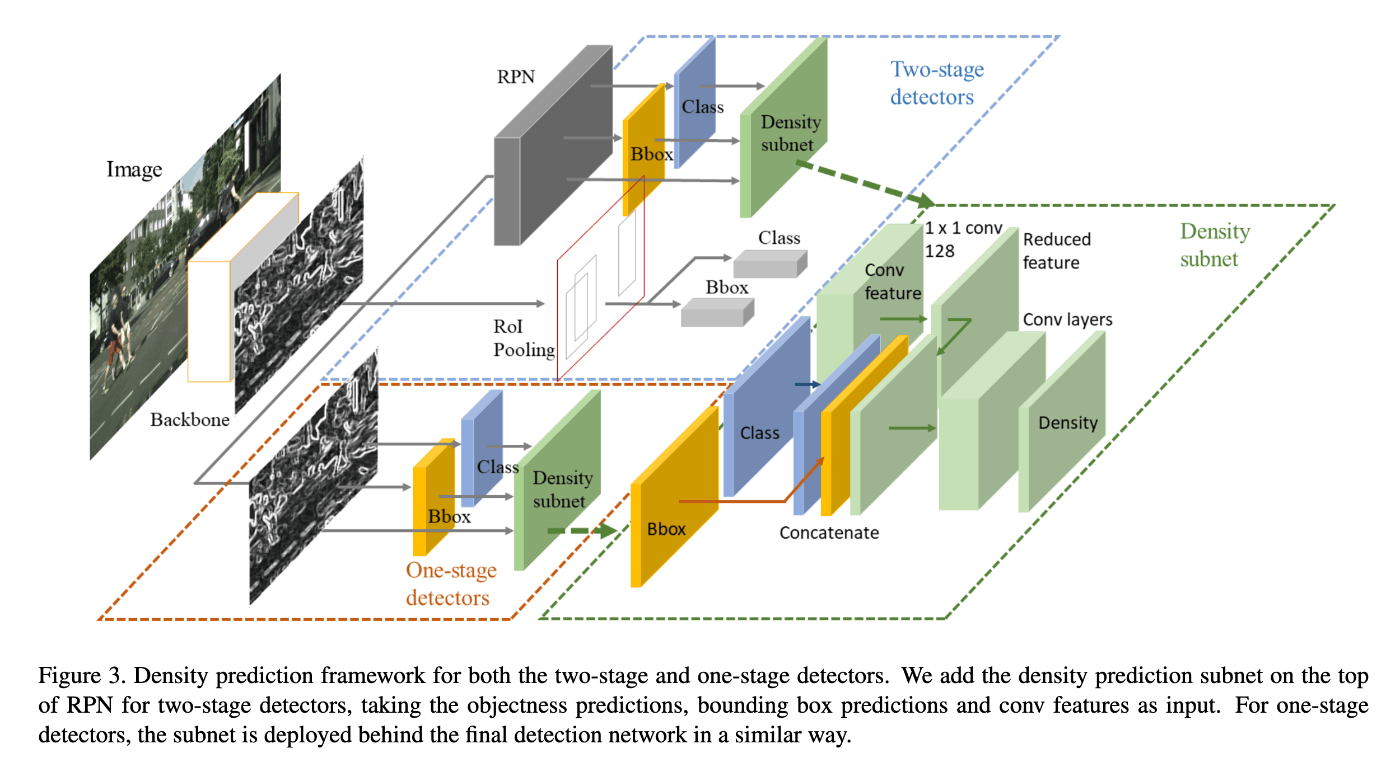
図1. density prediction headの構成 ([1]より転載)

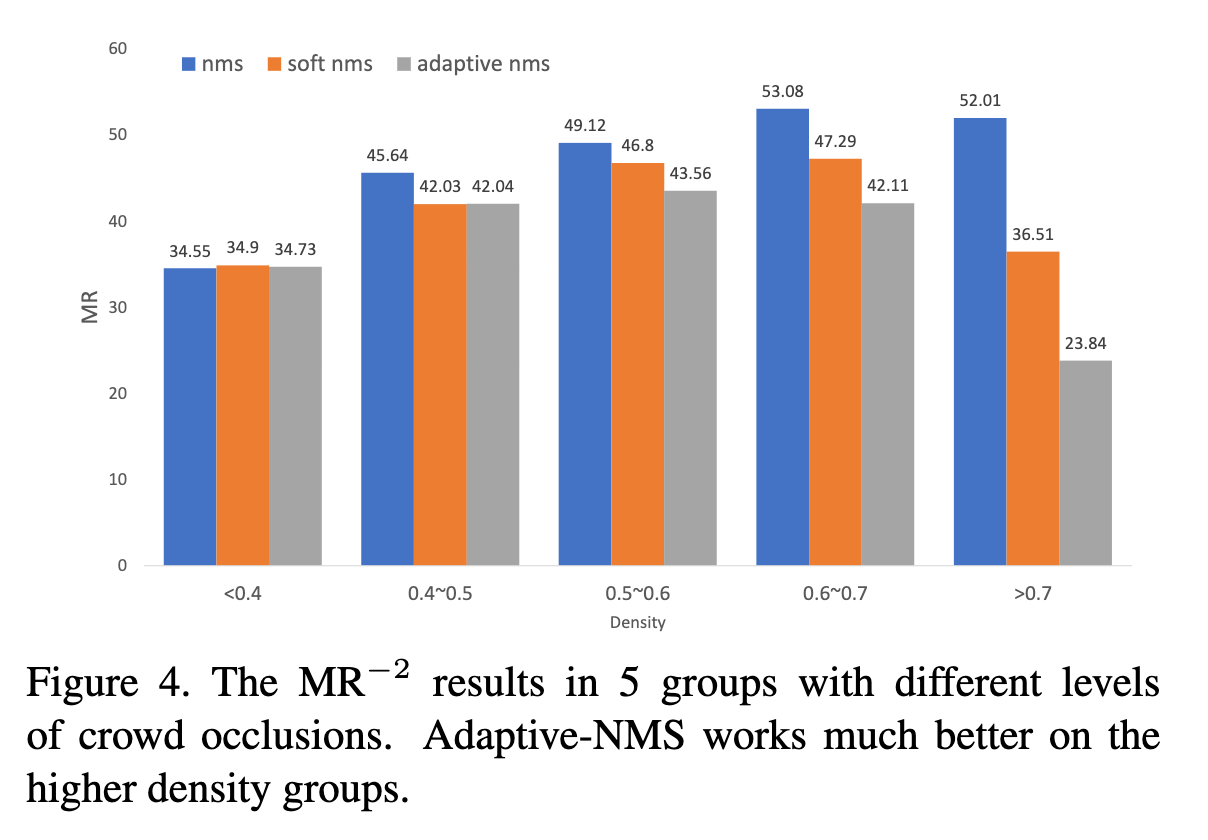
図2. 提案手法の混雑度ごとのMiss Rateの既存手法との比較 ([1]より転載)

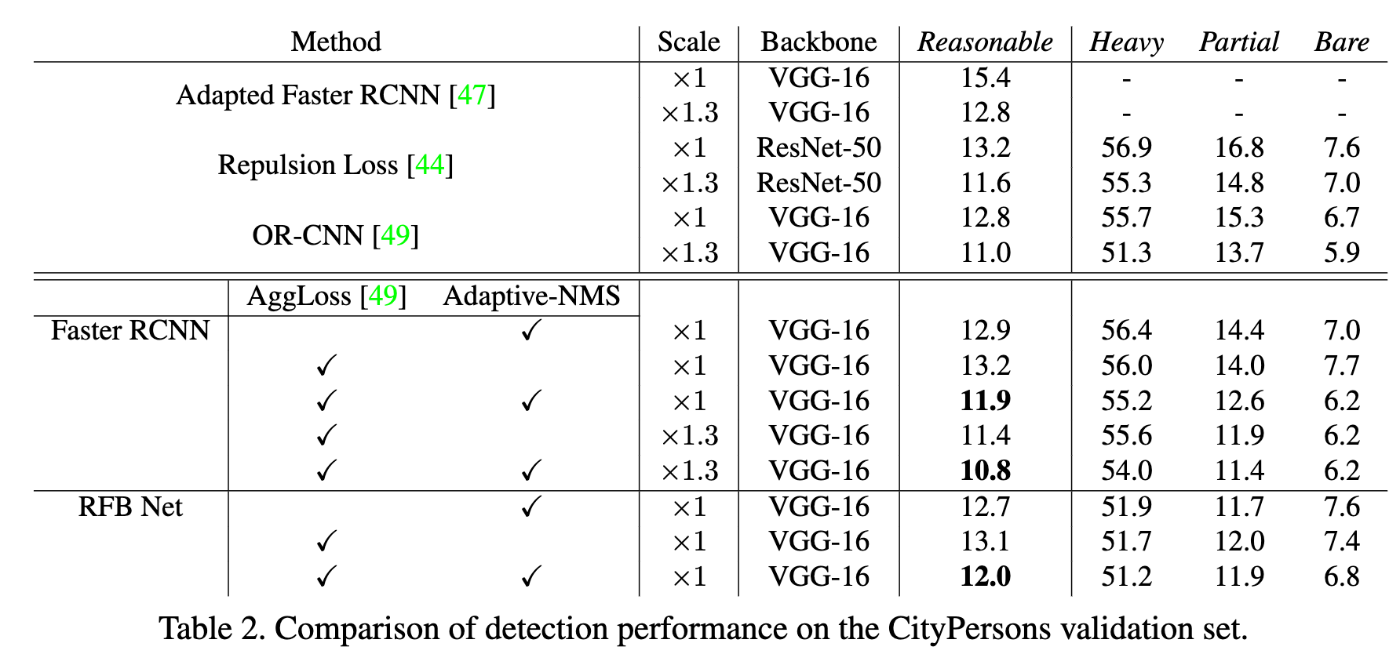
表1. GTサンプルのocclusionごとの既存手法と提案手法の性能比較 ([1]より転載)

AggLoss

予測boxの"まとまり"をよくする

PDタスクにおけるbox精度の改善手法として、AggLoss[5]という手法がある。

コンセプトとしては、GTに近いboxの集合がそのGT box周辺に"まとまった"状態にすることを目指したもので、以下のような補助的な損失(compact loss)を導入する。

$$\mathcal{L}_{\text{com}}(\{t_i\}, \{t_i^*\}) = \frac{1}{N_{\text{com}}} \sum_{i=1}^{N_\text{com}} \Delta(t_i^* - \frac{1}{|\Phi_i|} \sum_{j \in \Phi_i} t_j),$$

表記について、$t_i^*, t_i$ はそれぞれGTと予測boxの座標からなる4次元のベクトルを表す。$N_\text{com}$ はバッチ中のGT box数を表し、$\Phi_i$ は $g_i$ と重なる提案boxの集合を表す。また、$\Delta$ はSmooth-L1 lossで、以下のように定義される。

$$\Delta(t_i^*, t_i) := \begin{cases} \frac{1}{2} (t_i - t_i^*)^2, &\text{if } |t_i - t_i^*| < 1 \\ |t_i - t_i^*| - \frac{1}{2}, &\text{otherwise} \end{cases}$$

AggLossはGT boxに近い提案boxをグループとして捉え、それらを同じGTの座標に近づける、という意味を持つ^[2]。

Variance Voting (Softer-NMS)

[2]はBox座標の予測に確率的な表現を導入した回帰手法とそれを利用したSoft-NMS[4]の変種のアルゴリズム(Variance Voting; Softer-NMS)を提案する。

この論文ではMS-COCOデータセットにおけるラベルに一貫性がないケース(図3)に着目し、ラベルの不確実性を反映した回帰手法を提案する。

図3. MS-COCOデータセットにおける非一貫的なラベルの例 ([2]より転載)

Boxの座標を確率的な表現でモデル化する

具体的にはラベルの確率分布をGauss分布と仮定して以下のようにモデル化する。

$$P_{\Theta}(x) = \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(x - x_e)^2}{2\sigma^2}}$$

表記について、$x, x_e$ はそれぞれGTと推定したboxの座標を表す。$\Theta$ はモデルの学習可能なパラメータを表し、$x_e, \sigma$ を回帰するのに用いられる。

本手法は一般的なpoint回帰手法に用いられる確率的表現とは異なり、Gauss分布のパラメータ自体をNeural Networkにより回帰する。すなわち、Gauss分布の標準偏差 $\sigma$ を固定のハイパーパラメータとして定義するのでなく、モデルが動的に学習できるように設計されている。

ラベルはGauss分布ではなく以下のようにpoint-wiseに与える。すなわち、上記のGauss分布において $\sigma \rightarrow 0$ としたDiracのDelta関数を用いる^[3]。

$$P_D(x) = \delta(x - x_g)$$

損失関数にはKL divergence Lossを用いる。Delta関数(=one-hot表現)をラベルとした場合、KL divergence Lossは以下のようにL2 Lossに比例する項と$\sigma$ の肥大化を抑制する正則化項からなる損失関数に帰着する。

$$\mathcal{L}_\text{reg} \propto \frac{(x_g - x_e)^2}{2\sigma^2} + \frac{1}{2}\log(\sigma^2)$$

なお、上記の損失関数は$\sigma \rightarrow 0$ の場合に第一項、第二項共に発散することが懸念される^[4]。したがって実際に学習するさいは数値的な安定性を実現するために$\sigma$ を直接回帰せずにパラメータ $\alpha=\log(\sigma^2)$ を回帰する^[5]。また、$|x_g - x_e| > 1$ の区間ではL1損失を用いる(Soft-L1 Loss)。したがって最終的な損失関数はパラメータ$\alpha$ を用いて以下のように表現される。

$$\mathcal{L}_\text{reg} := \begin{cases} \frac{1}{2} e^{-\alpha} (x_g - x_e)^2 + \frac{1}{2} \alpha, & \text{if } |x_g - x_e| \le 1 \\ e^{-\alpha}(|x_g - x_e| - \frac{1}{2}) + \frac{1}{2} \alpha, & \text{otherwise} \\ \end{cases}$$

Variance Votingのアルゴリズムについて

次に、回帰予測のuncertainty ($\sigma$) の回帰結果を利用したSoft-NMSの改良版アルゴリズムであるVariance Votingについて説明する。

基本的なコンセプトはuncertaintyの度合いに基づいてMCB周辺のboxの座標を補正するというものである^[6]。

具体的には以下の式によりboxの座標を補正する。

$$\begin{align*} \hat{p}_{x, i} &= \frac{\exp(-(1-\text{IoU}(b_i, b_\mathcal{M})^2 / \sigma_t)}{\sigma_{x, i}^2}\\ x &= \frac{\sum_i \hat{p}_{x, i} x_i}{\sum_i \hat{p}_{x, i}}, \text{ s.t. } \text{IoU}(b_i, b_\mathcal{M}) > 0 \\ \end{align*}$$

上式における$\sigma_t$ はMCBと周辺のboxのIoUが補正結果に与える影響を制御するハイパーパラメータである。この式の分子はSoft-NMSにおいてMCBと周辺のboxとの重なりの度合いを表す尺度(Gaussian metric)であり、それを$\sigma_{x,i}^2$で割った形式になっている。つまり、uncertaintyの大きいサンプルほど補正結果への寄与が小さくなるように設計されている。$\sigma_{x, i}$の添字$x$ は、boxの座標ごとにuncertaintyを個別に回帰することを意味する（つまり、boxのtop, left, bottom, rightのそれぞれの座標予測に対するuncertaintyをモデル化している）。

Variance Votingの効果について

表2は異なるIoU thresholdのAPスコアに対して提案手法の効果を既存手法(NMS, Soft-NMS)と比較したものである。この表によれば、GTとの高い精度の回帰しか許容しないメトリクス(つまり$AP^x$の$x$が大きいもの)ほど提案手法の効果が顕著に現れていることがわかる。逆に低い精度を要求するAPメトリクスでは若干性能を犠牲にしている。

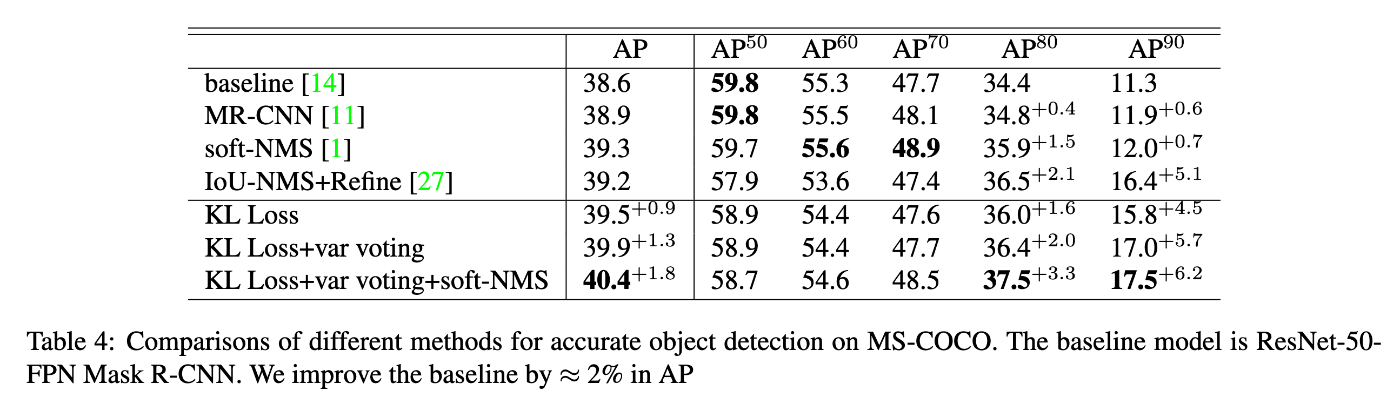
表2.IoU thresholdごとの提案手法の効果について ([2]より転載)

この結果によると、提案手法は高精度な回帰を実現するタスクに対してより効果的であることがわかる。
このような結果となった理由は個人的に以下のように考察している。

1. 提案手法はone-hot表現によるラベルを与えているため、uncertaintyが高いサンプルに対してはよりシャープな予測が可能であるため、L2損失などと比べて高精度の予測ができる。
2. 1の一方で、uncertaintyが低いサンプルに対してはよりぼやけた予測となり、lossへの寄与が小さくなるため、このようなサンプルによるnoiseの影響を抑えらえる。
3. Variance Votingは、Boxの座標の回帰結果を周辺のboxのuncertaintyに応じて補正することができる。これは、一部の座標(例: top, left, etc.)のみ回帰精度は良いが、他の座標の回帰精度が悪いboxの回帰結果を平均することにより、すべての座標について精度の高いboxを生成しやすいためだと考えられる。
4. また、提案手法はclassの予測精度とlocalityの予測精度を組み合わせた手法であるから、classの予測精度は高いがlocalityの予測精度は低いboxを過大に評価することを抑制する効果があり、結果としてclass予測精度とlocalityの予測精度が共に高いboxを残してそれ以外のboxを間引くことに成功しているためだと考えられる。

まとめ

本記事では、ODタスクにおけるpost-processing手法として、以下の3つの手法を紹介した。

1. PDタスクにおいて、GT boxが混み合った領域で適切にFPを間引くために、GT boxの混雑度(density)をNNモデルにより回帰し、それに基づいて(Soft-)NMSにおけるIoU thresholdを動的に決定する手法[1]。
2. モデルの予測boxの"まとまり"をよくするために、GT周辺の予測boxの座標の平均値をGTの座標に近づけるような補助的な損失関数を導入する手法[5]。
3. Boxのラベルの座標が一貫しないサンプルの悪影響を緩和するために、box座標を確率的な表現でモデル化し、得られたbox座標予測のuncertaintyを利用してNMSにおいてclass予測の精度とbox回帰の精度をともに加味して間引く手法。また、Soft-NMSにおいてconfidenceの補正に加え、MCB周辺の提案boxの回帰結果を平均してすべての座標の回帰予測精度とクラス予測の回帰予測精度が共に高精度な予測boxを生成する手法[2]。

Reference

• [1] Adaptive NMS: Refining Pedestrian Detection in a Crowd, 2019
• [2] Bounding Box Regression with Uncertainty for Accurate Object Detection, 2019
• [4] Soft-NMS -- Improving Object Detection With One Line of Code, 2017
• [5] Occlusion-aware R-CNN: Detecting Pedestrians in a Crowd, 2018
• [6] Fast R-CNN, 2015

脚注

1. この定義では2つのGT boxの重なりしか考慮していないが、3つ以上のGT boxからなる密度を反映するために、最大値でなくIoUの和で表現する定義も考えられる。

2. 「予測boxをコンパクトにする」ことが目標なので、個人的には回帰boxの平均をGTと近づけるよりも、GT boxと重なりのある回帰boxの集合の座標の分散を0に近づける方が個人的には直感に合うと感じた。

3. なお、このような数学的な表現は主に解析目的のために導入されるものなので、実際にはGTの座標を表す点に確率1が割り当てられていることに注意。

4. 直感的には指数関数のアクティベーション $e^x$ を用いて $x$ を適当な区間でclipすればその問題は回避されそうに思える。

5. 推論時には$\sigma=e^{\alpha/2}$ により復元する。

6. 周囲のboxのconfidenceを下げるだけでなく、周辺boxの座標を集約することでboxの座標も補正してしまおう、というのはWBF(Weighted Box Fusion)と似たような考え方である。