畳み込みのpaddingサイズの設計とpixelの位置ずれについて

概要

keypoint回帰など、1pixel単位の精密な回帰が求められるCNNモデルを設計する際、1pixelのずれが問題になる場合がある。
特に、strideが大きい場合や層数が深いネットワークではpixelの位置ずれは致命的な問題となりうる。
本稿ではpaddingの位置ずれがどのようにして起こるかを考察し、回避方法を示す。

以降では簡単のため、1次元のテンソルを考える。また、本稿ではdilationが1よりも大きいケースについては扱わない。

インデックスと数直線との対応

まず、テンソルのインデックスを数直線上のどの点に対応させるのが良いかを考察する。

数直線状の点$x$をテンソル上のインデックス$i$に一意に対応させる場合、そのインデックス$i$を$\text{index}(x)=i_x$と表記する。逆に、インデックス$i$を数直線上の点$x$にマッピングする場合は$\text{numeric}(i)=x_i$と表記する。

まず、ナイーブにindexの値と数直線上の値が一致するような対応を考える。すなわち、

$$x_i = \text{numeric}(i) = i$$

あるいは、

$$i_x = \text{index}(x) = \text{round}(x)$$

これはテンソルを1x1のピクセルとみなした場合に、その左端の点をテンソルのインデックスに対応させることに相当する(図1中央)。逆に、右端の点をテンソルのインデックスに対応させる場合は以下のようになる(図1下)。

$$x_i = \text{numeric}(i) = i + 1$$

あるいは、

$$i_x = \text{index}(x) = \text{round}(x) + 1$$

しかしながら、これらはともにflip変換で1pxのずれが生じるので好ましくない。したがって、ピクセルの中央の点をテンソルのインデックスと対応させるのが妥当である(図1下)。すなわち、

$$x_i = \text{numelic}(i) = i + 0.5$$

あるいは、

$$i_x = \text{index}(x) = \text{floor}(x)$$

図1. テンソルのインデックスと数直線上の点の対応

convolutionのpaddingサイズとpixelの位置ずれ問題について

この節ではstrideが1より大きい場合のpaddingサイズをどのように指定するのが良いかを考察する。

以降の議論では以下の要件を念頭においている。

1. flip変換に対して不変
2. 繰り返しconvolutionを適用しても位置ずれが拡大しない

なお、私が知る限り、paddingの計算には以下の2通りの計算式が使われているようである。

1. $p=(k-1)//2$
2. $p=(k-s)//2$

まず、1, 2の双方の意味について考察し、後者の方が前者よりも良いことを示す。

1. $p=(k-1)//2$によるpadding

これは、「convolution適用前のkernelの中心がインデックス0に対応する」ことを目的としたpaddingとみなすことができる（図2中央, 図3中央）。この方法ではconvolution適用前のインデックス0が適用後のインデックス0に対応するので、一見正しい対応方法に思える。しかしながら、この方法では以下に議論するようにpixelの位置ずれが生じる。

これには「convolution適用後のピクセル0が適用前のどのピクセルに対応させるのが妥当か？」という問題を考える。前の節で議論したように、テンソルのインデックスはピクセルの中央に対応するのが妥当だった。すなわち、適用後のインデックス0は、数直線上では0.5の点に対応する。仮に、stride=8だとすると、適用前は適用後の8倍の位置と対応するのだから、$0.5 \times 8=4$の点と対応するのが妥当である(図3下)。

2. $p=(k-s)//2$によるpadding

前小節で議論した内容を踏まえると、「convolution適用後のインデックス0に対応する適用前のインデックスの中心をカーネルの中心と一致させる」のが良いということになる。
つまり、

$$k \times 0.5 - p = s \times 0.5$$

すなわち、

$$p = (k - s) / 2$$

という対応が妥当である。実際はpaddingは整数値しか取りえないため、floor関数で整数に調整した$p = (k - s) // 2$により計算する。

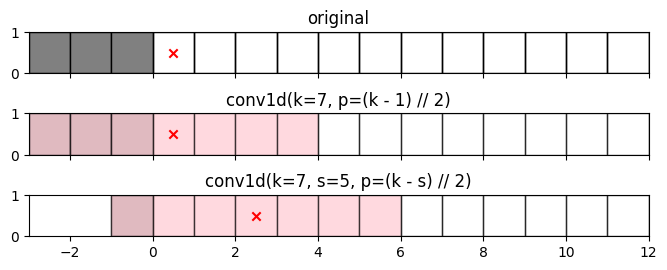
図2. k=7, s=5の場合のpaddingサイズ

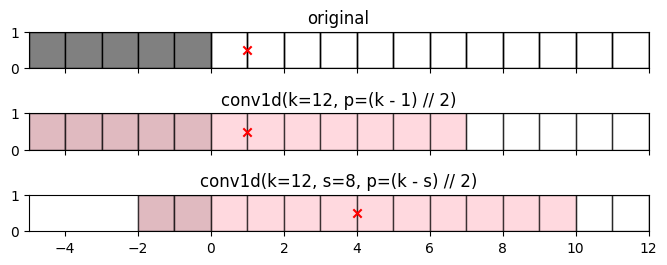
図3. k=12, s=8の場合のpaddingサイズ

padding sizeを設計する際の注意点

前節の議論により、strideが1より大きい場合は$p = (k - s) // 2$というpaddingが妥当であることを示した。
しかしながら、kernel sizeとstrideは自由に設計するよりも、両者の偶奇が一致するように設計するのが妥当であることを示しておく。

これは単純に、kとsの偶奇が異なる場合は$k - s$が奇数となり、2で割り切れないことに起因する。つまり、kernelの中心が正しい位置から0.5pxずれるためである。

まとめ

本稿では畳み込み演算におけるpadding sizeの設計について以下の内容について議論した。

1. 配列のindexは数直線上にマッピングする場合は「pixelのboxの中央」にalignするのが良い。
2. paddingサイズを計算する場合は$(k - 1) // 2$よりも$(k - s) // 2$の方が良い。
3. kernelサイズとpaddingサイズの偶奇は一致させる方が良い。