Zenn
😽

LLMの重みの量子化でパフォーマンスが改善する仕組みについて

2025/02/12に公開
LLM
awq
bilzardpaper
quantize
tech

Abstract

本記事では、重みの量子化でパフォーマンスが改善する仕組みについて、Rooflineという図を使って視覚的に説明する。前半ではパフォーマンスのボトルネックを可視化するRooflineという図の作図法と各領域の意味について説明する。後半ではRooflineを使ってなぜ重みの量子化がシステムのパフォーマンスを改善するのかについて、AWQの論文を例にして説明する。

なお、この記事でいうパフォーマンスとはシステムリソースの利用効率のことをさし、精度などのベンチマーク性能ではないことに注意。

Rooflineとは？

Rooflineとは、計算機システムのボトルネックを視覚的に判断するための図であり、ボトルネックが以下のどちらにあるのかを判断することができる。

  • memory-bound / bandwidth-bound: データの転送で詰まってて、GPUは暇を持て余している状態。
  • computing-bound: GPUの処理で詰まってて、メモリの帯域に余裕はあるがデータが送れてない状態。

Rooflineおよび計算機モデルの説明はNational Energy Research Scientific Computing Center(NERSC; 日本で言うとNEDOに相当するところ？)の資料[1a-1c]を参考にした。

単純化された計算機システムのモデル

以降の説明ではNERSCによるGPUの構造を極限にまで単純化したモデル[1b]を使って説明する。具体的には、Compute(GPU), PerfectCache, DRAM(VRAM) の3つの構成要素からなる。

このモデルでは、以下のような理想化された状態を仮定する。

  1. Compute (GPU)には単位時間あたりの処理速度に上限(GFLOP/s)がある
  2. Compute (GPU)とPerfect Cacheの間の帯域に上限はない
  3. Perfect ChaceとDRAM間のみ帯域の上限(GB/s)が存在する


(source: https://www.nersc.gov/assets/Uploads/RooflineHack-2020-RooflineModel.pdf)

Rooflineの描き方

まず、Throughput と Arithmetic Intensity の2軸からなるグラフを描く。

  • Throughput: 単位時間のタスク処理量。単位: FLOP/s
  • Arithmetic Intencity(AI): 転送したデータ量あたりのタスク処理量。単位: FLOP/Byte

次に、ここに以下の2つの直線を引く

  • GPUの計算速度の上限[FLOP/s]: ピンクの線
  • DRAMとPerfect Cache間の転送容量[GB/s]: 青線（勾配が転送容量に相当）


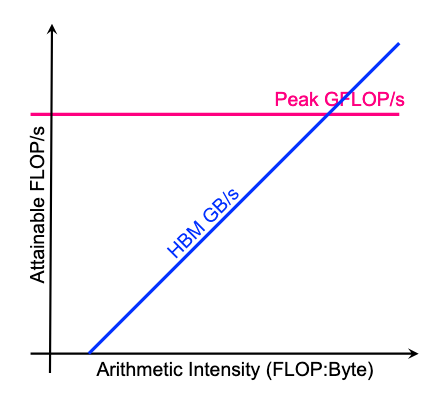
(source: https://www.nersc.gov/assets/Uploads/RooflineHack-2020-RooflineModel.pdf)

Roofline上の各領域の意味

図は以下の4つの領域に分けられる。

  1. unattainable performance: 青線、ピンク線の上側はHW的な制約によって実現不能な領域。
  2. bandwidth-bound (memory-bound): 青線のすぐ下あたり。
  3. computing-bound: ピンク線のすぐ下あたり。
  4. poor performance: 2つの線から下に離れた領域。計算機資源をフルに活用できてない。

パフォーマンス計測対象の計算機システムは、実現不能な領域以外のどこかの領域上の点として表現できる。一般的にはThroughputを上限まで高めたいので、図の右上の状態（＝GPU使用率100%）を目指すことがパフォーマンス改善の目的である。


(source: https://www.nersc.gov/assets/Uploads/RooflineHack-2020-RooflineModel.pdf)

モデルの重みの量子化による速度改善のメカニズム

ここまでの知識を使うと、モデルの量子化によってなぜパフォーマンス改善ができるのかを説明することができる。

以下ではAWQの論文[2]のFigure 3bをベースに説明する。ここからわかることは、

  • Context Stage(prefixを処理するstage)はcomputing-boundなので問題ない。
  • Generation Stage(回答を生成するstage)はmemory-boundになっている。

ここで、仮にモデルの重みを1/4に量子化してDRAMに保持し、perfect cacheとの間の転送負荷を1/4下げることができたと仮定すると、Arithmetic Intencityは4倍になるので、理論上のGPUの利用率が4倍になる。つまり、モデルの重みの量子化によって理論的には計算機リソースの利用率を上げることができる。

なお、元から生成タスクがcomputing-boundの場合はこのような改善は得られない。しかし、一般的なHWの性能改善のトレンドとして、処理性能のスケール速度の方がメモリ帯域のスケール速度よりも指数関数的に速いことが報告されている[3]ので、こういう状況は今後も頻繁に起こりうると考えられる。


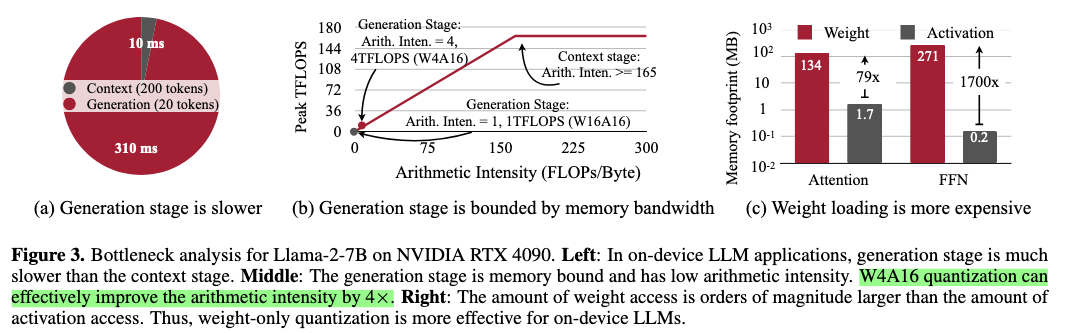
(source: https://arxiv.org/abs/2306.00978)

現実的なタスクでの評価

理論的なパフォーマンス改善の上限は上記のごとくだが、実際にデータ周りの処理はHWや低レベルのフレームワークの処理に依存する（例: DRAMとPerfect cacheの間を未圧縮のデータが行き来するかもしれない）し、dequantizeの処理のオーバーヘッドも追加されるので、一般的には理想的なゲイン以下になる。

AWQの論文ではA100を使った実験で3倍程度の速度改善が実現できたとしている（ただし、このデータには量子化以外の速度改善も含まれる）。

現実的に我々が体感できる速度改善としては、vLLMやLlama.cppといった推論エンジン側の最適化の進捗に依存している（あるいは独自で低レイヤの最適化を行うか）。


↑はAWQの論文[2]のTable 10をグラフにプロットしたもの。 (source: bilzard)

まとめ

  • モデルの重みの量子化によって速度改善が得られる仕組みをRooflineを使って説明した
  • 実行環境がmemory-boundな場合、重みの量子化は有効な速度改善手法となる
  • 実際のメモリ転送の処理はHWや低レベルのフレームワークに依存するので理論限界の性能は必ずしも出せないが、経験的に重みの量子化によって速度改善が得られることが報告されている。

図の著作権について

引用元がbilzard以外のものは全て引用元に著作権が帰属する。

Reference

GitHubで編集を提案

Discussion