論文読解: GRU4Recの改良 - 負例のサンプリングと損失関数の改良

論文

Recurrent Neural Networks with Top-k Gains for Session-based Recommendations

概要

時系列ベースの推薦モデルであるGRU4Recのロス関数と負例のサンプリング戦略を改良し、GRU4Recと比較してMRRとRecall＠20で最大35%の改良に成功した。

• GRU4Recの課題を改良した新しい損失関数を提案
• 負例のサンプリング方法を改良

前提知識

GRU4Recとは何か？

時系列ベースの推薦モデルの一種で、LSTMの簡易バージョンであるGRUを採用したもの。

Session-based Recommendations with Recurrent Neural Networks

時系列ベースの推薦モデルとは？

• あるユーザの商品に対するアクション（クリックした、カートに入れた、購入したなど）の時系列を入力として、次にユーザがアクションする商品を推測するモデルのこと（図1）。

  

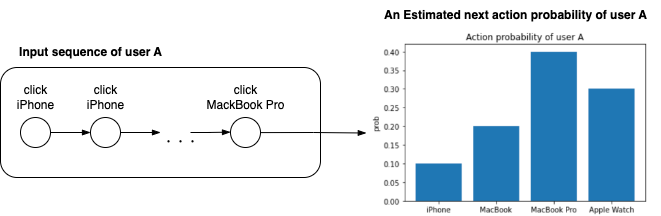
  図1.時系列ベースの推薦モデルの概念図

以下では以下の2点について記述する。

1. サンプル戦略の改良
2. 損失関数の改良

1. サンプル戦略の改良

サンプリングとは？

• 一般的な時系列推薦モデルは、入力シーケンスから出力の埋め込み表現を獲得し、全結合層を全商品のスコアを計算する。商品数が多くなってくる（〜1M）と全結合層の重みと計算コストが膨大になる。
• GRUのアーキテクチャ（図2）もこのパターンで、計算量は$O(N_E(H^2 + HN_O))$になる。ここで$N_E$: 学習データに含まれるイベント数、$N_O$: 最終出力層の数、$H$: 隠れ層のユニット数である。
• 計算量は商品数とイベント数の積に比例するので、大規模なデータセットに対してはスケールしなくなる。したがって最終層の商品から負例（＝実際にはアクションしなかった商品）を適宜間引くことで計算量を削減することを考える。
• なお、「サンプリング」といっても入力データのサンプルのことのではく、出力層の商品のサンプリングであることに注意。実際にやっていることは重みの更新に寄与するパラメータの選択である。

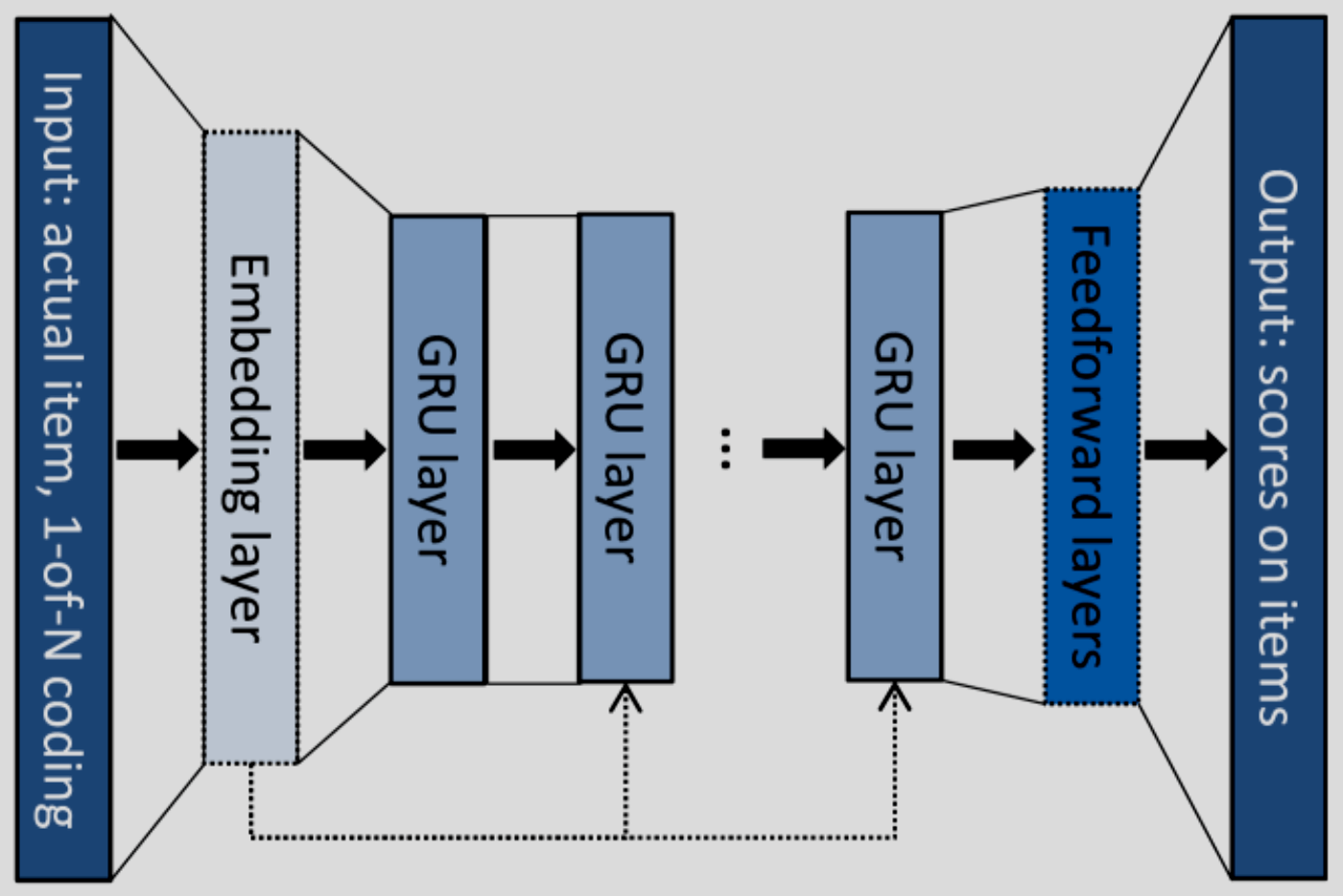
図2: GRU4Recのアーキテクチャ

負例のサンプリング戦略

一般的な負例のサンプリング戦略は以下の2つに分類される。

1. RNS(Random Negative Sampling): 一様分布によるサンプリング
2. PNS(Popularity-based Negative Sampling): 商品の頻度分布に基づくサンプリング

GRU4Recではミニバッチの中からサンプルしている。ミニバッチ内の商品の分布は全商品の分布と概ね一致するので、これはPNSの一種である。

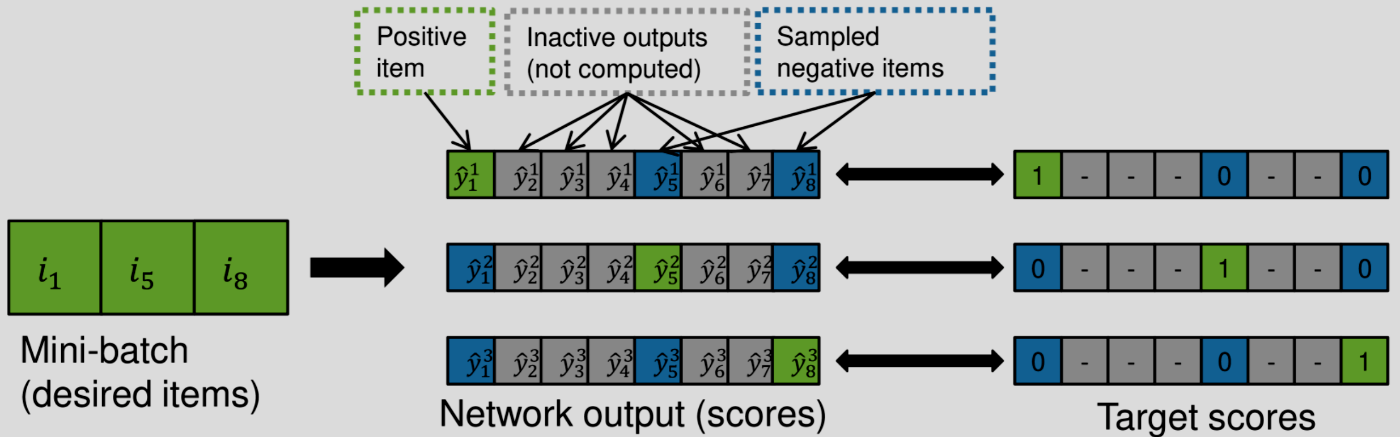
図3: ミニバッチサンプリングの概念図

ミニバッチサンプリングの課題

ミニバッチサンプリングは実用面で利便性が高いが、以下の課題もある。

1. バッチ数は高々数十〜数百である。全商品データ数が大きい場合は、学習に寄与するサンプルを見逃す可能性が高い
2. ミニバッチのサイズは学習結果に直接影響を与えるパラメータなので、サンプリングのパラメータとは分離したい
3. 自動的にpopularityに依存したサンプリングを選択することになるが、全てのデータセットでこの戦略が最適とは限らない

負例サンプルの追加

そこで、改良版のGRU4Recではミニバッチからサンプルした負例に加えて、全学習データからのサンプルを追加することで上記の課題を解決する。

$$X_B \propto f(X)^\alpha, \\\alpha \in [0, 1]$$

ここで$f$は商品$X$の頻度分布を表し、$\alpha$は分布をコントロールするパラメータである。$\alpha = 0$のときランダムサンプリングになり、$\alpha = 1$のとき純粋に頻度に比例するサンプリングとなる。

2. 損失関数の改良

GRU4Recの最初の論文ではBPR損失と、それをレコメンデーション向けに改良したTOP1損失を使っていた。改良版のGRU4Recではこれらの課題を分析し、改善したTOP1-max, BPR-max損失を提案する。

表記

以降では特に断りなく以下の表記を用いる。

• $i$: 正例のインデックス
• $j$: 負例のインデックス
• $r_i$: 商品スコア
• $N_s$: 負例のサンプル数
• $s_i$: 商品スコアのsoftmax

GRU4Recの損失関数

1) TOP1損失

$$\mathcal{L}_{TOP1} = \frac{1}{N_s}\sum_{j=1}^{Ns}\sigma(r_j-r_i) + \sigma(r_j^2)$$

2) BPR(Baysian Personalized Ranking)損失

$$\mathcal{L}_{BPR} = -\frac{1}{N_s}\sum_{j=1}^{Ns}\log\sigma(r_i-r_j)$$

学習に貢献する負例と貢献しない負例

論文では負例のスコアに応じて以下のような区別をしている。

• 学習に貢献する負例: $r_j > r_i$ - 勾配が大きい
• 学習に貢献しない負例: $r_j \gg r_i$ - 勾配がほぼ0

GRU4Recの損失関数の課題

• TOP1, BPRではいずれも「個々の負例の損失の平均」を計算している。これは負例のサンプル数が大きくなった場合に学習に貢献しない負例の割合が多くなり、平均した時の損失が小さくなることで学習が遅くなることが想定される。

改良版の損失関数

コアなアイデアとしては、「負例の損失を計算する際に平均でなく最大値を計算する」というもの。こうすることで、学習に貢献する負例の影響を強調することができ、学習が効率的に進むことが期待できる。

実際の損失の計算では、maxではなく微分可能なsoftmax関数を用いる。

ここでのsoftmaxは正例を除いた負例のサンプルのみで計算されていることに注意。

3) TOP1-max損失関数

$$\mathcal{L}_{TOP1-max} = \sum_{j=1}^{Ns}s_j(\sigma(r_j-r_i) + \sigma(r_j^2))$$

これは各負例の重みを平均値$1/N_s$からsoftmaxに変換しただけのもの。

4) BPR-max損失関数

$$\mathcal{L}_{BPR-max} = -\log\sum_{j=1}^{Ns}s_j(\sigma(r_i-r_j))$$

$P(r_i > \max(r_j))$を最大化するという発想で、以下の式から導出した確率に負の対数をとったもの。

$$P(r_i > r_{\max}) = P(r_i > r_j | r_j = r_{\max})P(r_j = r_{\max})) \\ \approx P(r_i > r_j)s_j$$

提案手法の評価

サンプル数の追加、および改良版の損失関数の効果を評価する。

図4はCLASSデータセットにおける、ベースラインと提案手法のパフォーマンスの比較である。TOP1は負例のサンプルを増やすと128くらいまではパフォーマンスが改善するが、以降は減少している。これは前述したようにサンプル数が増えたときに学習に寄与しない負例によって学習が妨げられていることを示唆する。TOP1-max, BPR-maxについては負例のサンプルを増やすほどパフォーマンスは増加していく傾向にある。

図5はサンプル数と学習時間の関係を表したものである。学習時間は追加のサンプル数が2048を超えたあたりから徐々に増加していくが、それ以下ではほぼ変わらず、GPUの並列処理で賄えていることを示している。

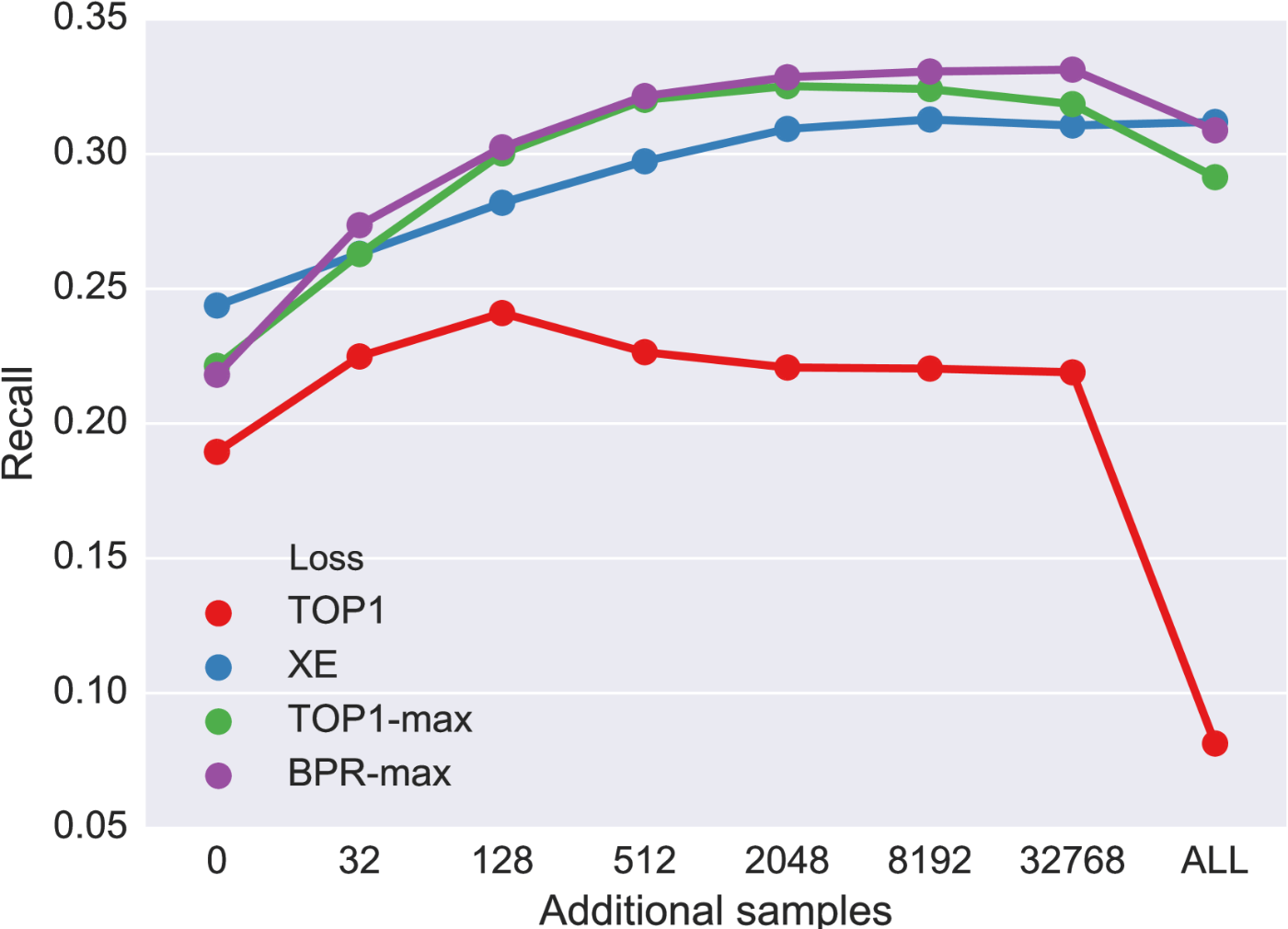
図4. パフォーマンスの比較（CLASS）

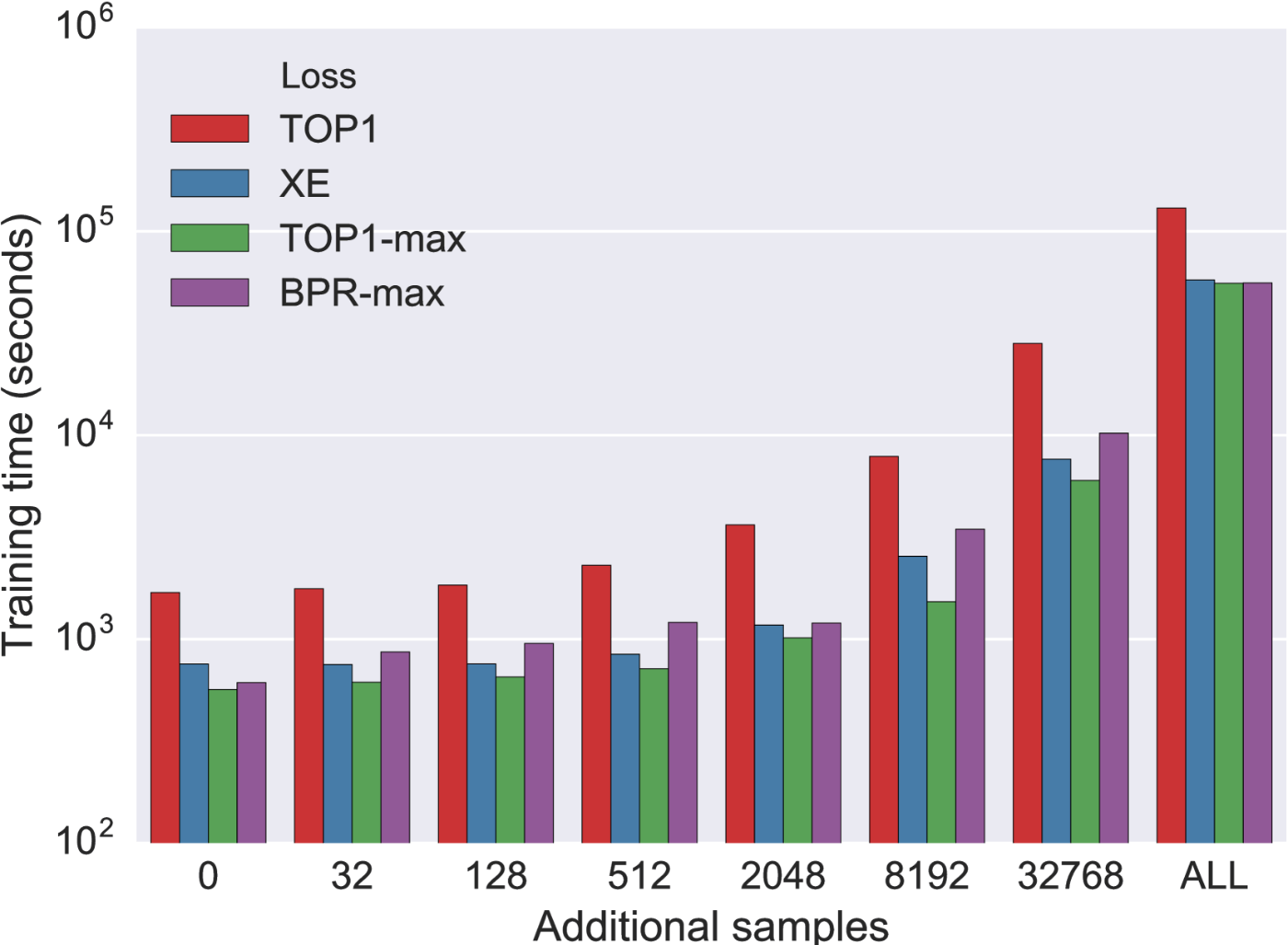
図5. サンプル数と学習時間の関係

まとめ

この記事では負例のサンプル戦略と損失関数を工夫することでGRU4Recのパフォーマンスを改善する方法についての論文の内容を解説しました。

所感としては、ネガティブサンプルというとデータセットを間引くイメージを持っていたので、最初は理解に苦労しましたが、出力層のパラメータのうち、逆伝搬させるパラメータを選択する手法のことを指していることがわかると色々とすんなりと理解することができました。