RNNが学習できるコンテクスト長についての考察

概要

本稿ではRNNが学習できるコンテクスト長について考察する。

「LSTMやGRUは素のRNNと比べて長期的なコンテクストを学習しやすい」と一般的に言われているが、具体的にどのような構造によってそのような性質を持つのか、また、どの程度「長期的な」コンテクストを学習できるのかについて数学的形式に基づいた洞察を得ることを目的とする。

本稿の成果は以下である。

1. 各種RNNのアーキテクチャの特徴と各構成要素の機能について直感的な解釈を示した
2. LSTMやGRUが素のRNNに比べて「長期的なコンテクストを学習しやすい」とする根拠について定義式に基づき議論した

RNNの各種アーキテクチャについて

まず、各種RNNのアーキテクチャごとの違いを整理する。
数学的表現および表記については[1]を参照した。

表記:

• $t$: 時系列のインデックス
• $x_t$: 入力信号の時系列
• $o_t$: 出力信号の時系列
• $h_t$: hidden stateの時系列
• $c_t$: cell stateの時系列

bare-RNN

本稿ではゲート構造を持たないRNNを後続のアーキテクチャと区別するためにbare-RNNと呼称する。

特徴:

• hidden state ($h_i$)に過去の系列の積算としてコンテクストを保持する。
• 現在のhidden stateは現在の系列と直前のhidden stateに応じて決まる。
• 一般的に「長期にわたるコンテクストは学習できない」とされている。

数学的表現:

$$h_t = \tanh(W_{x} x_t + W_{h} h_{t-1} + b)$$

ダイヤグラム:

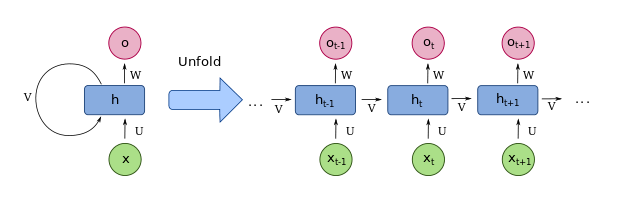
Attribution: fdeloche, CC BY-SA 4.0 https://creativecommons.org/licenses/by-sa/4.0, via Wikimedia Commons

LSTM

特徴:

bare-RNNの長期的なコンテクストを学習できない問題に対処するために提案された。
伝搬させる信号そのものと制御信号(gate)を分離したことで過去の信号の影響の減衰に関してbare-RNNよりも解釈性が高いアーキテクチャになっている。

過去の系列を保持する変数として hidden state ($h_t$)に加えて cell state ($c_t$)）を導入し、それぞれshort-time memory,long-time memoryに対応する役割を果たす。

また、以下の3つのgateで過去の系列と現在の系列の伝搬量をコントロールする:

• forget gate ($f_t$): cell stateの伝搬量をコントロールする
• input gate ($i_t$): 現在の系列の伝搬量をコントロールする
• output gate ($o_t$): hidden stateの伝搬量をコントロールする

数学的表現:

$$\begin{align*} f_t &= \sigma(W_{f,x} x_t + W_{f,h} h_{t-1} + b_f) \\ i_t &= \sigma(W_{i,x} x_t + W_{i,h} h_{t-1} + b_i) \\ o_t &= \sigma(W_{o,x} x_t + W_{o,h} h_{t-1} + b_o) \\ c_t &= f_t \odot c_{t-1} + i_t \odot \tanh(h_{t-1}) \\ h_t &= o_t \odot \tanh(c_t) \\ \end{align*}$$

ダイヤグラム:

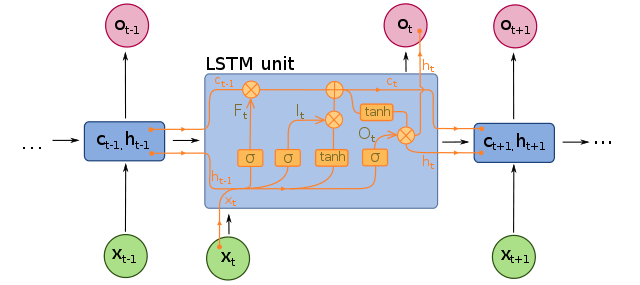
Attribution: fdeloche, CC BY-SA 4.0 https://creativecommons.org/licenses/by-sa/4.0, via Wikimedia Commons

GRU

特徴:

状態変数とゲートの数を減らしてLSTMを簡素化したもの。

以下の2つのgateでコンテクストと現系列それぞれの伝搬量をコントロールする:

• reset gate ($r_t$): 直前のcell stateの伝搬量をコントロールする
• update gate ($u_t$): 現在の系列と直前のcell stateの混合の割合をコントロールする

数学的表現:

$$\begin{align*} r_t &= \sigma(W_{r,x} x_t + W_{r,h} h_{t-1} + b_r) \\ u_t &= \sigma(W_{u,x} x_t + W_{u,h} h_{t-1} + b_u) \\ \hat{h}_t &= \tanh(W_{g,x} x_t + W_{g,h} (r_t \odot h_{t-1}) + b_g) \\ h_t &= u_t \odot h_{t-1} + (1 - u_t) \odot \hat{h}_t \end{align*}$$

ダイヤグラム:

Attribution: fdeloche, CC BY-SA 4.0 https://creativecommons.org/licenses/by-sa/4.0, via Wikimedia Commons

RNNが学習できるコンテクスト長について

RNNが学習できるコンテクスト長について議論する。
最初に概念的・直感的な考察を示し、最後に定義式に基づいたより厳密な議論をする。

基本となるアイデア

以降では「RNNが学習できるコンテクスト長」について議論を進めるが、前提として、「back propagationの計算において目的関数の勾配がどの程度初期の時系列ステップに対応するブロックに伝搬するか」を考える。すなわち、対象とする系列を$\{z_i\}$とするとき、$\partial L/\partial z_i$が過去の時系列に対応するステップに逆伝搬するにあたってどのように変化していくかに着目する。前方に伝わる前に勾配が十分小さくなったり、無限大に発散するならば「ネットワークは長期のコンテクストを加味した学習が原理的にできない」というのが基本的な考え方である。

これと似た考え方に、「ネットワークがどの程度の長さのコンテクスト情報を保持するか」という問題があるが、ここではこの問題については扱わない。

なぜbaer-RNNは「長期的なコンテクストを学習できない」か？

bare-RNNが長期のコンテクストを学習できない原因は端的にいうと「勾配消失・爆発しやすいため前方のステップまで勾配が伝搬しないため」であるが、LSTMやGRUも勾配はステップを遡るともに減少するので両者の違いを議論するには数式に基づく議論が必要である。
直感的にはbare-RNNにおいては「制御信号と信号そのものが分離されていない」ことが長期的なコンテクストを学習できないことについての間接的な原因であり、具体的にはback propagation で時系列を遡るたびにtanhのパスを繰り返し通ることで同じ係数行列の線形変換が勾配に冪乗されて適用され、勾配爆発・消失のいずれかが生じやすくなることが原因と考えられる。

LSTMやGRUが「長期的なコンテクストを学習できる」のはなぜか？またどの程度「長期的」か？

これに対し、後継のアーキテクチャであるLSTMやGRUは制御信号(ゲート)と信号そのものが分離されている。ゲートは「信号をどの程度後続のステップに伝搬させるか」をコントロールする。具体的には信号そのものに$(0, 1)$区間に正規化されたゲート信号を乗じるという数学的形式を持つ。これはステップを重ねるごとに減衰率 $f_t \in (0, 1)$ を元信号に乗じているとみなすことができる。この係数はback propagation の計算時も勾配に同じ量が乗じられる。$0 < f_t < 1$であるから勾配の伝搬量はステップを遡るたびに単調減少するが、 $f_t$ は定数でなく入力系列に依存して決まるため、「データに基づいて減衰の度合いをコントロールする」ことができる。このため、bare-RNNに比べると勾配の減衰が抑えられれ、より長期的なコンテクストを学習しやすいと考えられる。

勾配の減衰に関するより厳密な議論

以上の議論を数式に基づきより厳密に議論する。

RNNにおける勾配の減衰

bare-RNNにおけるhidden stateについての勾配の計算式は以下のようになる。

$$\begin{align*} \frac{\partial L}{\partial h_t} &= \frac{\partial L}{\partial h_{t+1}} \cdot \frac{\partial h_{t+1}}{\partial h_t} \\ &= \frac{\partial L}{\partial h_{t+1}} \cdot W_{h} \cdot \left(1 - \tanh^2\left(W_{x} \cdot x_t + W_{h} \cdot h_{t-1} + b_h\right)\right) \end{align*}$$

前方のステップに遡るたびに$W_h(1-\tanh^2(\cdot))$の部分が繰り返し乗算されるため、$\|W_h\|\ne1$の場合、$W_h$の項はステップを遡るとともに指数関数的に減衰/増加する。$1 - \tanh^2(\cdot)$の項については減衰の度合いを入力系列に応じて適応できるが、ステップを重ねるにつれて$W_h$の項が支配的となり、勾配爆発か勾配消失のいずれかが生じやすくなると考えられる(注1)。

---

注1: $\|W_h\|\approx 1$とする制約を加えればbare-RNNにおいても勾配爆発・消失の問題はある程度緩和できるかもしれない。[3]では$\|\partial L / \partial h_{t+1} \cdot \partial h_{t+1} / h_t \| \approx \| \partial L / \partial h_{t+1} \|$とする制約項によってこの問題に対処している(付録A)。

LSTMにおける勾配の減衰

LSTMにおけるcell stateについての勾配の計算式は以下のようになる。

$$\begin{align*} \frac{\partial L}{\partial c_t} &= \frac{\partial L}{\partial h_{t+1}} \cdot \frac{\partial h_{t+1}}{\partial c_t} + \frac{\partial L}{\partial c_{t+1}} \cdot \frac{\partial c_{t+1}}{\partial c_t} \\ \frac{\partial c_{t+1}}{\partial c_t} &= f_{t+1} = \sigma(W_{f,x} x_{t+1} + W_{f,h} h_{t} + b_f) \\ \end{align*}$$

前方のステップに遡るたびに乗算されるのは$f_{t+1} \in (0, 1)$ の部分であるから、勾配はステップを遡るとともに単調減少する。

bare-RNNとの違いは2つあり、まず、乗算される項が$(0, 1)$区間に収まっているので勾配爆発が回避されている。また、bare-RNNにおける乗数項$W_h$が定数なのに対し、LSTMの乗数項$f_{t+1}$は入力系列$\{x_t\}$に依存する。このため、LSTMではデータに基づいて「減衰を強めたり抑えたり」するようにパラメータを学習する余地が残されており、勾配消失がより生じにくいと考えられる。

Reference

• [1] A Brief Introduction to Recurrent Neural Networks
• [2] Bengio, Y., Simard, P., and Frasconi, P. (1994). Learning long-term dependencies with gradient descent is difficult. IEEE Transactions on Neural Networks, 5(2), 157–166.
• [3] Pascanu, P., Mikolov, T., and Bengio, Y. (2013). On the difficulty of training Recurrent Neural Networks
• [4] Hochreiter, S. and Schmidhuber, J. (1997). Long short-term memory. Neural Computation, 9(8), 1735–1780

付録

付録A: 勾配消失・爆発問題に関する研究論文について

勾配消失・爆発の問題についての既存研究について触れておく。勾配消失・爆発の問題は歴史が古く、1994年にはすでにBengioらによって提起されている[2]。比較的最近(2013年)に出版された論文には[3]があり、本稿で扱ったような議論（重み行列の冪乗のノルムが勾配伝搬とともに指数関数的に減少・増大する）をよりフォーマルに論じている。また、この論文では逆伝搬される勾配のノルムの増加と減少に対してペナルティを加える正則化項$\Omega$を導入することでこの問題を解決することを提案している(「逆伝搬によりノルムの大きさが概ね一定となる」ような制約であり、逆伝搬による作用素$\|\partial h_{t+1} / \partial h_t\|$自体を1に近づける制約ではないことに注意):

$$\Omega = \sum \Omega_k = \sum_k \left( \frac{\left\| \frac{\partial L}{\partial h_{t+1}} \cdot \frac{\partial h_{t+1}}{\partial h_t} \right\|}{\left\|\frac{\partial L}{\partial h_{t+1}} \right\|} - 1 \right)^2$$

この論文でトークン列の分類タスクにおいて、長さ50〜200の時系列に対して提案手法によりSGDによる学習の成功確率が向上することを示した。

一方で、LSTMの論文[4]では1,000を超える系列長の人工データ対して模擬的なタスクを十分な性能で行えることを実験により示している。