bellbind 2022/09/01に更新

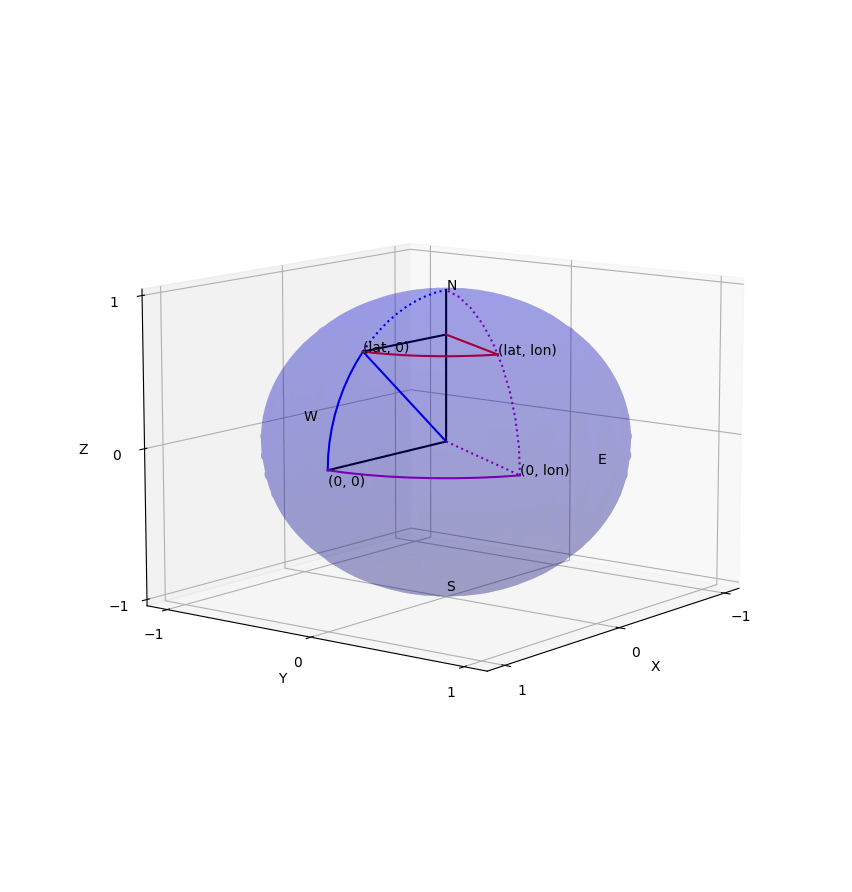
緯度(latitude)と経度(longitude)が判っている2点の距離の導出。

半径1球体の中心 $O$ を $(0,0,0)$ 、北極の座標を $(0, 0, 1)$ とし、北緯0東経0の点を $(1, 0, 0)$ 、北緯0東経90の点を $(0, 1, 0)$ とする座標系を用いる(西経や南緯はマイナス角度)
このとき、緯度 $P$ のz座標は $\sin P$ 、緯度 $P$ での(赤道面と平行な)円の半径は $\cos P$ になる
よって緯度 $P$ 経度 $Q$ の点の座標は $(\cos P\cos Q, \cos P\sin Q, \sin P)$ である
2点の距離は、2点と中心 $O$ を含む(半径1の)大円上での2点のラジアン角度 $t$ そのものである
半径1なので大円上の2点の中心からの長さは1であり、その内積は $\cos t$ である
緯度 $P_1$ 経度 $Q_1$ と緯度 $P_2$ 経度 $Q_2$ の二点の内積は、3の座標値より、
$\cos P_1\cos P_2\cos Q_1\cos Q_2 + \cos P_1\cos P_2\sin Q_1\sin Q_2 + \sin P_1\sin P_2$
である
よって $\cos t = \cos P_1\cos P_2\cos Q_1\cos Q_2 + \cos P_1\cos P_2\sin Q_1\sin Q_2 + \sin P_1\sin P_2$
よって $t = \arccos(\cos P_1\cos P_2\cos Q_1\cos Q_2 + \cos P_1\cos P_2\sin Q_1\sin Q_2 + \sin P_1\sin P_2)$
地球上での距離は地球の平均半径6371000mを $t$ にかけることで求まる

緯度経度

この手法は回転楕円体である地球では厳密ではない。しかし、少ない計算で求まる利点がある。
(さらに三角関数の加法定理で、 $\cos Q_1\cos Q_2 + \sin Q_1\sin Q_2 = \cos(Q_1-Q_2)$ を使うと積が一つ減らせる)

const distance = ([lat1, lon1], [lat2, lon2]) => {
  const {PI, acos, sin, cos} = Math, rad = PI / 180, r = 6371000;
  const [p1, p2, q1, q2] = [lat1, lat2, lon1, lon2].map(v => v * rad);
  return r * acos(cos(p1) * cos(p2) * cos(q1 - q2) + sin(p1) * sin(p2));
};

bellbind 2022/04/20に更新

地球の平均半径の導出。

平均半径は、楕円体を同じ体積の真の球体とみなしたときの半径のこと。
球の体積は $\frac{4\pi r^3}{3}$
楕円体はx軸y軸z軸ごとに別々の経をもち、それぞれa,b,cとすると、体積は $\frac{4\pi abc}{3}$
この2つを等しいとみなすことによって、平均半径 $r = \sqrt[3]{abc}$
地球は球の上下を少し潰したもの(回転楕円体)とみなし、a=b=6378137m、c=6356752mである
地球の平均半径は6371000.685...m

const a = 6378137, c = 6356752;
const r = Math.cbrt(a * a * c);

bellbind 2022/04/21に更新

haversine法

$\text{hav}(x) = \frac{1 - \cos x}{2}$ と定義する
緯度経度表示の二点の内積より

\begin{aligned} \cos t &= \cos P_1\cos P_2\cos Q_1\cos Q_2 + \cos P_1\cos P_2\sin Q_1\sin Q_2 + \sin P_1\sin P_2 \\ &= \cos P_1\cos P_2 (\cos Q_1\cos Q_2+\sin Q_1\sin Q_2)+\sin P_1\sin P_2 \\ &= \cos P_1\cos P_2\cos(Q_1-Q_2) + \sin P_1\sin P_2 \end{aligned}

$\cos x =1-2\text{hav}(x)$ より、 $1-2\text{hav}(t)=\cos P_1\cos P_2(1-2\text{hav}(Q_1-Q_2))+\sin P_1\sin P_2$
更に変形していくと、

\begin{aligned} 1-2\text{hav}(t) &= \cos P_1\cos P_2+\sin P_1\sin P_2-2\cos P_1\cos P_2\text{hav}(Q_1-Q_2) \\ &= \cos(P_1-P_2)-2\cos P_1\cos P_2\text{hav}(Q_1-Q_2) \\ &= 1-2\text{hav}(P_1-P_2)-2\cos P_1\cos P_2\text{hav}(Q_1-Q_2) \end{aligned}

よって $\text{hav}(t)=\text{hav}(P_1-P_2)+\cos P_1\cos P_2\text{hav}(Q_1-Q_2)$

$y=\text{hav}(x)$ の逆関数 $x=\text{hav}^{-1}(y)$

$\text{hav}^{-1}(y) = \arccos(1 - 2y)$

const distance = ([lat1, lon1], [lat2, lon2]) => {
  const {PI, acos, cos} = Math, rad = PI / 180, r = 6371000;
  const hav = x => (1 - cos(x)) / 2, ihav = y => acos(1 - 2 * y);
  const [p1, p2, q1, q2] = [lat1, lat2, lon1, lon2].map(v => v * rad);
  return r * ihav(hav(p1 - p2) + cos(p1) * cos (p2) * hav(q1 - q2));
};

haversine法では、cos/acosだけで計算できる(cos表があれば手計算できる)。

bellbind 2022/04/21に更新

geodesic inverse/direct

https://vldb.gsi.go.jp/sokuchi/surveycalc/surveycalc/algorithm/bl2st/bl2st.htm

上記リンクの途中のcは球面での内積そのもの。「ゾーンの判断」以降補正していくよう。

逆解法(inverse)が二点から距離とそれぞれの方位角を求める方法で、順解法(direct)が1点と方位角と距離で行き先を求める方法。

bellbind 2022/09/01に更新

緯度経度同士での方角

緯度 $P_1$ 経度 $Q_1$ から緯度 $P_2$ 経度 $Q_2$ への向きとは、 $(P_1, Q_1)$ から中心 $O$ への射影面上にある $O$ から $(P_2, Q_2)$ への向きである
経度差 $dQ=Q_2-Q_1$ とすると、 $y$ の値を0に調整した $(P_1, Q_1)$ のxyz座標は $(\cos P_1, 0, \sin P_1)$ 、 $(P_2, Q_2)$ のxyz座標は $(\cos P_2\cos dQ, \cos P_2\sin dQ, \sin P_2)$
$(P_1, Q_1)$ を座標 $(1, 0, 0)$ に移す回転はY軸周りで $-P_1$ 度回転させることである
Y軸 $-P_1$ 度回転の行列は

\begin{pmatrix} \cos P_1 & 0 & \sin P_1 \\ 0 & 1 & 0\\ -\sin P_1 & 0 & \cos P_1 \end{pmatrix}

$(P_2, Q_2)$ にY軸 $-P_1$ 度回転をかけた結果は、

\begin{pmatrix} \cos P_1 & 0 & \sin P_1 \\ 0 & 1 & 0\\ -\sin P_1 & 0 & \cos P_1 \end{pmatrix} \begin{pmatrix} \cos P_2\cos dQ \\ \cos P_2\sin dQ \\ \sin P_2 \end{pmatrix} = \begin{pmatrix} \cos P_1\cos P_2\cos dQ +\sin P_1\sin P_2 \\ \cos P_2\sin dQ \\ -\sin P_1\cos P_2\cos dQ + \cos P_1\sin P_2 \end{pmatrix}

X軸の先から中心へ眺めるYZ平面上での $(P_2, Q_2)$ の位置は、 $(Y, Z) = (\cos P_2 \sin dQ, -\sin P_1\cos P_2\cos dQ + \cos P_1\sin P_2)$
北を0度、東を90度とする場合の方角 $a$ とすると、 $\tan a = \frac{\cos P_2\sin dQ}{-\sin P_1\cos P_2\cos dQ + \cos P_1\sin P_2}$
よって、 $a = \text{atan2}(\cos P_2\sin dQ, -\sin P_1\cos P_2\cos dQ + \cos P_1\sin P_2)$
atan2の戻り値は $(-\pi, \pi]$ を返すので、 $[0, 360)$ 度に変えるには $\pi$ を足してから180を掛け $\pi$ で割る

const angle = ([lat1, lon1], [lat2, lon2]) => {
  const {PI, sin, cos, atan2} = Math, rad = PI / 180;
  const [p1, p2, q1, q2] = [lat1, lat2, lon1, lon2].map(v => v * rad);
  const dq = q2 - q1, cosP2 = cos(p2);
  const y = cosP2 * sin(dq);
  const z = cos(p1) * sin(p2) - sin(p1) * cosP2 * cos(dq);
  return atan2(y, z);
};

ちなみに、この方位はメルカトル図法(円筒モデル)上での向きではない。2点の最短距離の線(大円)の向きである。

bellbind 2022/04/28に更新

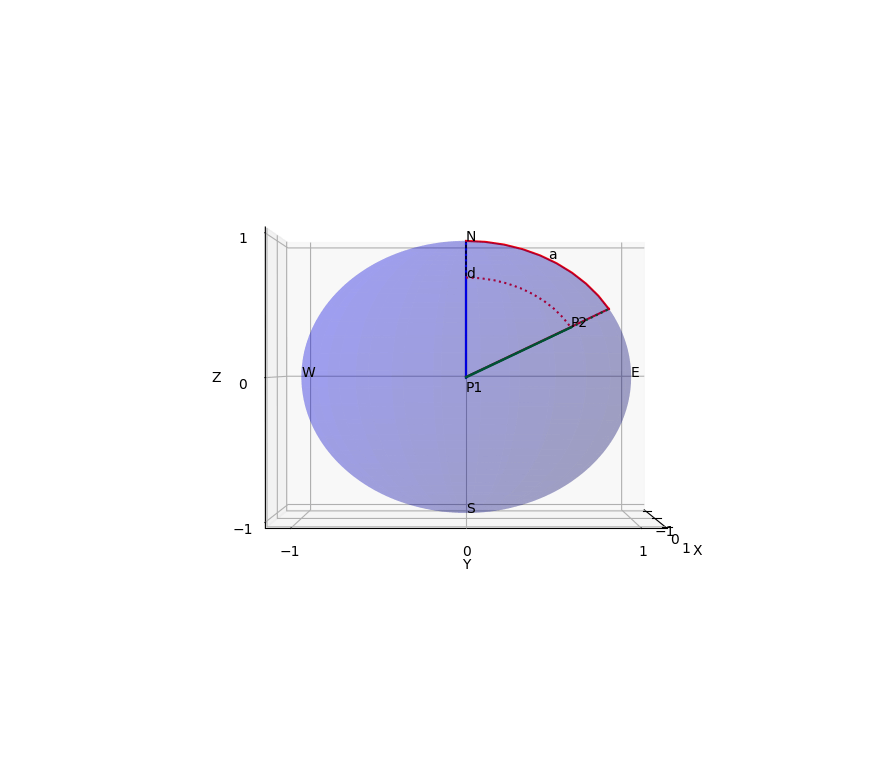
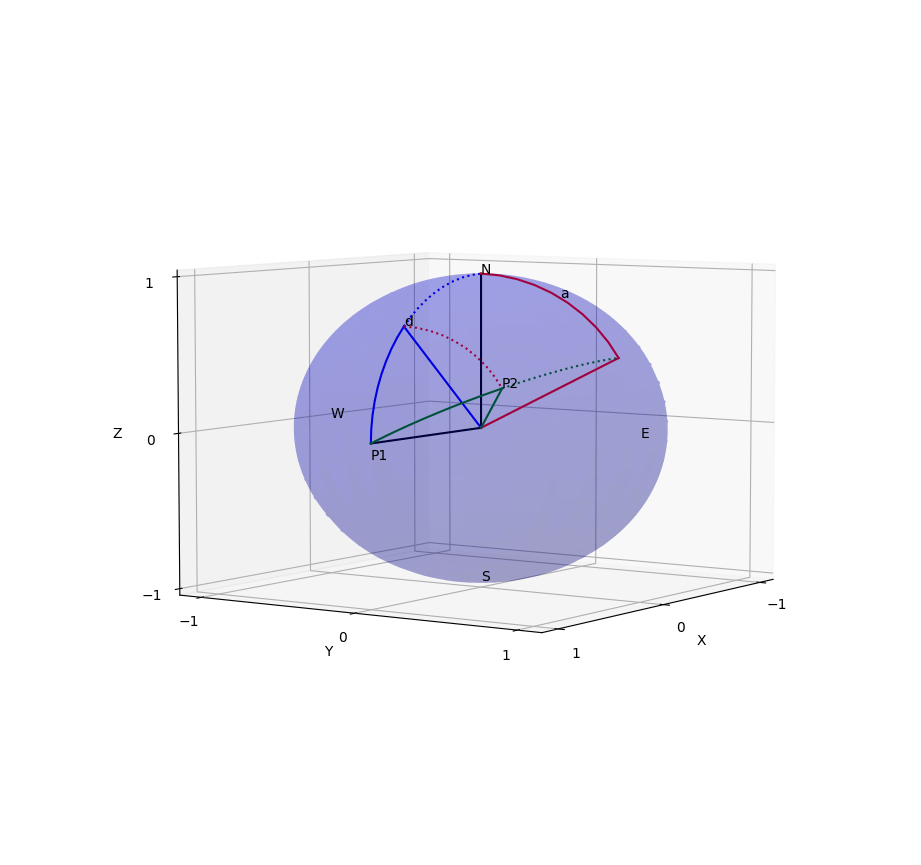
起点の緯度経度 $(P_1, Q_1)$ と方角と距離の先の緯度経度 $(P_2, Q_2)$ の求め方

半径1の単位球では、距離 $d$ の移動とは、角度 $d$ ラジアン回転させた先に移ることである(一周回れば $2\pi$ 移動する)
球の半径が $R$ のときの距離 $d$ の移動とは、角度 $\frac{d}{R}$ ラジアン回転させた先である( $d=2\pi R$ 移動させれば一周して戻ってくる)
単位球の北極を $(0, 0, 1)$ 、起点を $(1, 0, 0)$ 、起点の経度+90度を $(0, 1, 0)$ とするとき、 $(1, 0, 0)$ から角度 $a$ (真北が0度で時計回りに増加)の向きに距離 $d$ の移動とは、Y軸を反時計回りに $d$ ラジアン回転し、そのあとでX軸を時計回りに $a$ ラジアン回転させることに等しい
そこからさらにY軸反時計回りに緯度ぶんの $P_1$ (のラジアン値の)回転させれば、目的のxyz座標に移動する

(以降、計算式では $P_1$ 、 $Q_1$ 等はラジアン値に変換したものとして扱う)

この座標値と、方角を求めたときの $(P_2, dQ)$ のの座標値と比較することで、緯度 $P_2$ と経度の差 $dQ$ が求まる
Y軸反時計回り $s$ ラジアンの回転行列 $Y_s$

Y_s = \begin{pmatrix}\cos s & 0 & -\sin s \\ 0 & 1 & 0 \\ \sin s & 0 & \cos s\end{pmatrix}

X軸時計回り $t$ ラジアンの回転行列 $X_t$

X_t = \begin{pmatrix} 1 & 0 & 0\\ 0 & \cos t & \sin t \\ 0 & -\sin t & \cos t \end{pmatrix}

$I=(1, 0, 0)$ とすると、移動先は $Y_{P_1} X_a Y_d I$
行列計算すると

Y_{P_1} X_a Y_d I = (\cos P_1\cos d - \sin P_1\sin d\cos a, \sin d\sin a, \sin P_1\cos d + \cos P_1\sin d\cos a)

この値と、方角のときの $(P_2, Q_2)=(\cos P_2\cos dQ, \cos P_2\sin dQ , \sin P_2)$ と比較させる
- $\cos P_2\cos dQ = \cos P_1\cos d - \sin P_1\sin d\cos a$
- $\cos P_2\sin dQ = \sin d\sin a$
- $\sin P_2 = \sin P_1\cos d + \cos P_1\sin d\cos a$
まず緯度 $P_2 = \arcsin(\sin P_1 \cos d + \cos P_1\sin d \cos a)$ が求まる
つぎに、 $\sin dQ$ と $\cos dQ$ ともに $\cos P_2$ がかかっており、 $\cos P_2$ が0のときに計算できなくなるので、 $\tan dQ = \frac{\sin dQ}{\cos dQ}$ として、atan2を用いて $dQ$ を算出する

$dQ = \text{atan2}(\sin d\sin a, \cos P_1\cos d - \sin P_1\sin d\cos a)$

経度 $Q_2 = Q_1 + dQ$
どちらもラジアンなので360度に変換する

$\text{緯度} = \frac{P_2 \times 180}{\pi}$
$\text{経度} = (\frac{Q_2 \times 180}{\pi} + 360) % 360 - 180$

X軸からの射影

球面上の回転変換

// angleは真北0時計回りのラジアン
// distanceはメートル
const destination = ([lat1, lon1], angle, distance) => {
  const {PI, sin, cos, asin, atan2} = Math;
  const r = 6371000, rad = PI / 180;
  const d = distance / r, p1 = lat * rad, q1 = lng * rad;
  const p2 = asin(sin(p1) * cos(d) + cos(p1) * sin(d) * cos(angle));
  const q2 = q1 + atan2(sin(angle) * sin(d), cos(p1) * cos(d) - sin(p1) * sin(d) * cos(angle));
  return [p2 / rad, (q2 / rad + 360) % 360 - 180];
};

atan2(y, x)の引数2つにともに $\cos P_1$ を掛けても同じ結果になるので、さらに

上辺y: $\cos P_1 \sin d\sin a$
下辺x: $\cos P_1\cos P_1\cos d - \cos P_1\sin P_1\sin d\cos a = \cos d -\sin P_1\sin P_1\cos d - \sin P_1\cos P_1\sin d\cos a$
先のZ値の対比 $\sin P_2 = \sin P_1\cos d + \cos P_1\sin d\cos a$ を用いることで、下辺x: $\cos d -\sin P_1\sin P_2$

よって以下の様に変形し、演算回数を(掛け算ひとつ)減らすことができる

const destination = ([lat1, lon1], angle, distance) => {
  const {PI, sin, cos, asin, atan2} = Math, r = 6371000, rad = PI / 180;
  const d = distance / r, p1 = lat * rad, q1 = lng * rad;
  const cosP1 = cos(p1), sinP1 = sin(p1), cosD = cos(d), sinD = sin(d);
  const sinP2 = sinP1 * cosD + cosP1 * sinD * cos(angle);
  const p2 = asin(sinP2);
  const q2 = q1 + atan2(cosP1 * sinD * sin(angle), cosD - sinP1 * sinP2);
  return [p2 / rad, (q2 / rad + 360) % 360 - 180];
};

bellbind 2022/04/07に更新

参考: 前述の画像生成用のスクリプト(python3, numpy, matplotlib)

Demo on Google Colab: https://colab.research.google.com/drive/1zckfZKqwxYHy2kG4JVXi0srn1fff4Mm2?usp=sharing

latlng.py

import numpy as np
import matplotlib.pyplot as plt

fig = plt.figure()
ax = fig.gca(projection="3d")
ax.set_xlabel("X")
ax.set_ylabel("Y")
ax.set_zlabel("Z")
ax.set_xticks([-1, 0, 1])
ax.set_yticks([-1, 0, 1])
ax.set_zticks([-1, 0, 1])

def sphere():
    u = np.linspace(0, 2 * np.pi, 100)
    v = np.linspace(0, np.pi, 100)
    x = np.outer(np.cos(u), np.sin(v))
    y = np.outer(np.sin(u), np.sin(v))
    z = np.outer(np.ones(np.size(u)), np.cos(v))
    ax.plot_surface(x, y, z, rstride=4, cstride=4, color="b", linewidth=0, alpha=0.2)
    pass
sphere()

p = np.pi / 4
q = np.pi / 3

ax.plot([0, 1], [0, 0], [0, 0], color="black")
ax.plot([0, 0], [0, 0], [0, 1], color="black")

# lat
ax.plot([0, np.cos(p)], [0, 0], [0, np.sin(p)], color="b")
ax.plot(np.cos(np.linspace(0, p, 10)), np.zeros(10), np.sin(np.linspace(0, p, 10)), color="b")
ax.plot(np.cos(np.linspace(p, np.pi/2, 10)), np.zeros(10), np.sin(np.linspace(p, np.pi/2, 10)), linestyle="dotted", color="b")

# lng
ax.plot([0, np.cos(p)], [0, 0], [np.sin(p), np.sin(p)], color="black")
ax.plot([0, np.cos(p) * np.cos(q)], [0, np.cos(p) * np.sin(q)], [np.sin(p), np.sin(p)], color="r")
ax.plot(np.cos(p) * np.cos(np.linspace(0, q, 10)), np.cos(p) * np.sin(np.linspace(0, q, 10)), np.sin(p) * np.ones(10), color="r")

ax.plot([0, np.cos(q)], [0, np.sin(q)], [0, 0], linestyle="dotted", color="m")
ax.plot(np.cos(np.linspace(0, q, 10)), np.sin(np.linspace(0, q, 10)), np.zeros(10), color="m")
ax.plot(np.cos(np.linspace(0, np.pi/2, 10)) * np.cos(q), np.cos(np.linspace(0, np.pi / 2, 10)) * np.sin(q), np.sin(np.linspace(0, np.pi/2, 10)), linestyle="dotted", color="m")


#ax.text(0, 0, 0, "O")
ax.text(0, 0, 1, "N")
ax.text(0, 0, -1, "S")
ax.text(0, 1, 0, "E")
ax.text(0, -1, 0, "W")
ax.text(1, 0, -0.1, "(0, 0)")
ax.text(np.cos(p), 0, np.sin(p), "(lat, 0)")
ax.text(np.cos(q), np.sin(q), 0, "(0, lon)")
ax.text(np.cos(p) * np.cos(q), np.cos(p) * np.sin(q), np.sin(p), "(lat, lon)")


ax.view_init(elev=18, azim=0)
plt.show()

destination.py

import numpy as np
import matplotlib.pyplot as plt

fig = plt.figure()
ax = fig.gca(projection="3d")
ax.set_xlabel("X")
ax.set_ylabel("Y")
ax.set_zlabel("Z")
ax.set_xticks([-1, 0, 1])
ax.set_yticks([-1, 0, 1])
ax.set_zticks([-1, 0, 1])

def sphere():
    u = np.linspace(0, 2 * np.pi, 100)
    v = np.linspace(0, np.pi, 100)
    x = np.outer(np.cos(u), np.sin(v))
    y = np.outer(np.sin(u), np.sin(v))
    z = np.outer(np.ones(np.size(u)), np.cos(v))
    ax.plot_surface(x, y, z, rstride=4, cstride=4, color="b", linewidth=0, alpha=0.2)
    pass
sphere()

d = np.pi / 4
a = np.pi / 3

ax.plot([0, 1], [0, 0], [0, 0], color="black")
ax.plot([0, 0], [0, 0], [0, 1], color="black")

# distance
ax.plot([0, np.cos(d)], [0, 0], [0, np.sin(d)], color="b")
ax.plot(np.cos(np.linspace(0, d, 10)), np.zeros(10), np.sin(np.linspace(0, d, 10)), color="b")
ax.plot(np.cos(np.linspace(d, np.pi/2, 10)), np.zeros(10), np.sin(np.linspace(d, np.pi/2, 10)), linestyle="dotted", color="b")

# angle
ax.plot([0, 0], [0, np.sin(a)], [0, np.cos(a)], color="r")
ax.plot(np.zeros(10), np.sin(np.linspace(0, a, 10)), np.cos(np.linspace(0, a, 10)), color="r")

# mix
ax.plot([0, np.cos(d)], [0, np.sin(a) * np.sin(d)],[0, np.cos(a) * np.sin(d)], color="g")
ax.plot(np.cos(np.linspace(0, d, 10)), np.sin(a) * np.sin(np.linspace(0, d, 10)), np.cos(a) * np.sin((np.linspace(0, d, 10))), color="g")
ax.plot(np.cos(np.linspace(d, np.pi/2,10)), np.sin(a) * np.sin(np.linspace(d, np.pi/2, 10)), np.cos(a) * np.sin((np.linspace(d, np.pi/2, 10))), linestyle="dotted", color="g")

ax.plot([np.cos(d)] * 10, np.sin(np.linspace(0, a, 10)) * np.sin(d), np.cos(np.linspace(0, a, 10)) * np.sin(d), linestyle="dotted", color="r")

#ax.text(0, 0, 0, "O")
ax.text(0, 0, 1, "N")
ax.text(0, 0, -1, "S")
ax.text(0, 1, 0, "E")
ax.text(0, -1, 0, "W")
ax.text(1, 0, -0.1, "P1")
ax.text(np.cos(d), 0, np.sin(d), "d")
ax.text(0, np.sin(a/2), np.cos(a/2), "a")
ax.text(np.cos(d), np.sin(a) * np.sin(d), np.cos(a) * np.sin(d), "P2")


ax.view_init(elev=18, azim=0)
plt.show()

bellbind 2022/04/21に更新

付録1: 内積と角度

二次元の点 $(x_1, y_1)$ と点 $(x_2, y_2)$ の内積は $x_1 x_2+y_1 y_2$ 。
点を中心 $(0, 0)$ からの角度 $a$ と長さ $r$ とで表現すると、 $(r \cos a, r \sin a)$ 。
$\cos$ の加法定理の一つ: $\cos a \cos b +\sin a\sin b = \cos(a-b) = \cos(b-a)$
二点を $(r_1 \cos a_1, r_1 \sin a_1)$ 、 $(r_2 \cos a_2, r_2 \sin a_2)$ としたとき、それらの内積は、 $r_1 r_2 \cos a_1 \cos a_2 +r_1 r_2\sin a_1\sin a_2 = r_1 r_2\cos(a_1-a_2)$
$a_1-a_2$ は二点の間の角度。二点を同時に回転させ、座標を変えても二点の間の角度の値は変わらない

3次元の場合

一つ目の点を $P_1=(r_1, 0, 0)$ 、2つ目を $P_1$ とXZ平面上で中心 $O$ で角度 $a$ をなす点 $P_2=(r_2 \cos a, 0, r_2 \sin a)$ とすると、二点と中心で作る面の法線は $(0, 1, 0)$ となる
2点を目的の位置に調整することは、法線の座標を球面上の適当な位置へ移動させることである。これは、はじめZ軸つぎにY軸の適当な角度での二回転を適用することで可能。

Z軸回転

Z=\begin{pmatrix}\cos z & -\sin z & 0 \\ \sin z & \cos z & 0 \\ 0 & 0 & 1 \end{pmatrix}

Y軸回転

Y=\begin{pmatrix} \cos y & 0 & -\sin y \\ 0 & 1 & 0 \\ \sin y & 0 & \cos y \end{pmatrix}

YZ=\begin{pmatrix} \cos y \cos z & -\cos y\sin z & -\sin y\\ \sin z & \cos z & 0 \\ \sin y\cos z & -\sin y\sin z & \cos y \end{pmatrix}

\begin{aligned} YZP_1 &= r_1 \times (\cos y\cos z, \sin z, \sin y\cos z) \\ YZP_2 &= r_2 \times (\cos y\cos z\cos a-\sin y\sin a, \sin z\cos a, \cos z\sin y\cos a + \cos y\sin a) \end{aligned}

\begin{aligned} \text{内積値} &= r_1 r_2 \times(\cos^2 y \cos^2 z\cos a -\cos y\cos z\sin y\sin a +\sin^2 z\cos a+\sin^2 y\cos^2 z\cos a+\sin y\cos z\cos y\sin a) \\ &= r_1 r_2 \cos a \times (\cos^2 z (\cos^2 y+\sin^2 y)+\sin^2 z) \\ &= r_1 r_2 \cos a \end{aligned}

よって3次元でも、(2点がどんな位置にあろうがその)内積は二点の角度aに基づく値となる

付録2: 弧度法

角度を0-2πとする弧度法とは、角度を半径の長さを1とする単位円上の弧の長さで表現したもの

bellbind 2022/04/26に更新

Vincenty法

Wikipediaにある実装をそのまま適用

https://en.wikipedia.org/wiki/Vincenty's_formulae

vincenty.js

export const wgs84 = Object.freeze({
  a: 6378137.06,
  b: 6356752.314245,
  f: 1 / 298.257223563,
});
export const grs80 = Object.freeze({
  a: 6378137,
  b: 6356582.314,
  f: 1 / 298.257222101,
});

// Vincenty formula: https://en.wikipedia.org/wiki/Vincenty%27s_formulae
export const inverse = ([lat1, lon1], [lat2, lon2], {a, b, f} = wgs84,  eps = Number.EPSILON) => {
  const {abs, atan, atan2, cos, sin, tan, PI, sqrt} = Math;
  const P1 = lat1 / 180 * PI, P2 = lat2 / 180 * PI, L = (lon2 - lon1) / 180 * PI;
  const U1 = atan((1 - f) * tan(P1)), U2 = atan((1 - f) * tan(P2));
  const sinU1 = sin(U1), cosU1 = cos(U1), sinU2 = sin(U2), cosU2 = cos(U2);
  const cosU1sinU2 = cosU1 * sinU2, sinU1cosU2 = sinU1 * cosU2, sinU1sinU2 = sinU1 * sinU2, cosU1cosU2 = cosU1 * cosU2;
  for (let l = L, i = 0; i < 1000; i++) {
    const sinL = sin(l), cosL = cos(l);
    const sinD = sqrt((cosU2 * sinL) ** 2 + (cosU1sinU2 - sinU1cosU2 * cosL) ** 2);
    const cosD = sinU1sinU2 + cosU1cosU2 * cosL;
    const D = atan2(sinD, cosD);
    const sinA = cosU1cosU2 * sinL / sinD;
    const cos2A = 1 - sinA ** 2;
    const cos2Dm = cosD - 2 * sinU1sinU2 / cos2A;
    const C = f / 16 * cos2A * (4 + f * (4 - 3 * cos2A));
    const cos22Dm = cos2Dm ** 2;
    const l_ = l;
    l = L + (1 - C) * f * sinA * (D + C * sinD * (cos2Dm + C * cosD * (-1 + 2 * cos22Dm)));
    if (abs(l - l_) < eps) {
      //console.log(i);
      const a2 = a ** 2, b2 = b ** 2, sin2D = sinD ** 2;
      const u2 = cos2A * (a2 - b2) / b2;
      const A = 1 + u2 / 16384 * (4096 + u2 * (-768 + u2 * (320 - 175 * u2)));
      const B = u2 / 1024 * (256 + u2 * (-128 + u2 * (74 - 47 * u2)));
      const dD = B * sinD * (cos2Dm + B / 4 * (cosD * (-1 + 2 * cos22Dm) - B / 6 * cos2Dm * (-3 + 4 * sin2D) * (-3 + 4 * cos22Dm)));
      const s = b * A * (D - dD);
      const A1 = atan2(cosU2 * sinL, cosU1sinU2 - sinU1cosU2 * cosL);  // dir at latlon1
      const A2 = atan2(cosU1 * sinL, -sinU1cosU2 + cosU1sinU2 * cosL); // dir at latlong2, but dir from latlon1 to latlon2
      return {s, A1, A2, a1to2: (A1 / PI * 180 + 360) % 360, a2to1: (A2 / PI * 180 + 180) % 360};
    }
  }
  throw Error();
};

export const direct = ([lat1, lon1], a1, s, {a, b, f} = wgs84, eps = Number.EPSILON) => {
  const {abs, atan, atan2, cos, sin, tan, PI, sqrt} = Math;
  const P1 = lat1 / 180 * PI, L1 = lon1 / 180 * PI, A1 = a1 / 180 * PI;
  const tanU1 = (1 - f) * tan(P1);
  const U1 = atan(tanU1);
  const cosU1 = cos(U1), sinU1 = sin(U1), cosA1 = cos(A1), sinA1 = sin(A1);
  const D1 = atan2(tanU1, cosA1);
  const sinA = cosU1 * sinA1;
  const cos2A = 1 - sinA ** 2;
  const u2 = cos2A * (a ** 2 - b ** 2) / (b ** 2);
  const A = 1 + u2 / 16384 * (4096 + u2 * (-768 + u2 * (320 - 175 * u2)));
  const B = u2 / 1024 * (256 + u2 * (-128 + u2 * (74 - 47 * u2)));
  const D0 = s / b / A;
  for (let D = D0, i = 0; i < 1000; i++) {
    const sinD = sin(D), cosD = cos(D);
    const cos2Dm = cos(2 * D1 + D);
    const cos22Dm = cos2Dm ** 2, sin2D = sinD ** 2;
    const dD = B * sinD * (cos2Dm + B / 4 * (cosD * (-1 + 2 * cos22Dm) - B / 6 * cos2Dm * (-3 + 4 * sin2D) * (-3 + 4 * cos22Dm)));
    const D_ = D;
    D = D0 + dD;
    if (abs(D - D_) < eps) {
      //console.log(i);
      const P2 = atan2(sinU1 * cosD + cosU1 * sinD * cosA1, (1 - f) * sqrt(sinA ** 2 + (sinU1 * sinD - cosU1 * cosD * cosA1) ** 2));
      const l = atan2(sinD * sinA1, cosU1 * cosD - sinU1 * sinD * cosA1);
      const C = f / 16 * cos2A * (4 + f * (4 - 3 * cos2A));
      const L = l - (1 - C) * f * sinA * (D + C * sinD * (cos2Dm + C * cosD * (-1 + 2 * cos22Dm)));
      const L2 = L + L1;
      const A2 = atan2(sinA, -sinU1 * sinD + cosU1 * cosD * cosA1); // dir at latlong2, but dir from latlon1 to latlon2
      return {latlon2: [P2 / PI * 180, L2 / PI * 180], A2, a2to1: (A2 / PI * 180 + 180) % 360};
    }
  }
  throw Error();
};

方位角が2つあるのは、回転楕円体のため、同じ直線でも、緯度経度1を中心に置いて見る角度と、緯度経度2を中心に置いて見る角度は違うから。二点の間を結ぶ直線が2つあるわけではない。

また、atan2で出す角度A1とA2はどちらも、真北を0真東をπ/2とした、緯度経度1から緯度経度2へ向かう直線の方角である。緯度経度2から緯度経度1への方角にするには反転させるために180度足す。