ポアソン2項分布とは何か

ベルヌーイ分布と2項分布の関係を勉強している時に、成功確率pがそれぞれのベルヌーイ試行で異なっていたら、どうなるのだろうと調査したら、ポアソン2項分布というものがあった。

ベルヌーイ分布と2項分布の関係

ベルヌーイ分布とは、「成功か失敗か」「表か裏か」「勝ちか負けか」のように２種類のみの結果で表される事象の結果に、{0,1} の確率変数を振り分けたときの分布である。

1である確率がpであるとき0である確率は1-pとなる、非常にシンプルな確率分布。

二項分布とは、ベルヌーイ試行をn回トライアルした時の合計の確率分布。

式で表すと、

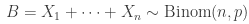
なおX_iはi.i.d
(zenでうまくLateX形式で数式を表示できないので、詳しい人ご教授ください)

ポアソン2項分布

それに対して、

$${ X_1, X_2, ..., X_n }$$

がそれぞれ異なる成功確率のベルヌーイ分布に従っている時

$$\text{Ber}(p_i)$$

その合計はポアソン2項分布に従う
確率質量関数は、組み合わせの合計になるため、F_kをサイズが k の { 0, 1,　 ... , n} の全ての部分集合の集合を表すことすると
ポアソン2項分布の確率質量関数は、

$$\begin{aligned} \mathbb{P}(B = k) &= \sum_{A \in F_k} \prod_{i \in A} p_i \prod_{j \notin A} (1- p_j). \end{aligned}$$

期待値と分散は、独立した確率変数の合計なので、

$$\begin{aligned} \mathbb{E}[B] &= \sum_{i=1}^n \mathbb{E}[X_i] = \sum_{i=1}^n p_i, \\ \text{Var} (B) &= \sum_{i=1}^n \text{Var} (X_i) = \sum_{i=1}^n p_i(1-p_i). \end{aligned}$$

従って2項分布は

$$p_1 = p_2 = ... = p_n$$

の時のポアソン2項分布の特殊ケースである

Rで可視化

library(poibin)

// 成功確率ベクトルをランダムに作成

> pp <- runif(100)
> pp
  [1] 0.753080000 0.790214698 0.761132775 0.035491509 0.163281161 0.147371607
  [7] 0.336843826 0.762204716 0.768641776 0.851757715 0.592781797 0.459652954
 [13] 0.756503935 0.671878833 0.897169144 0.388607557 0.236523256 0.845674027
 [19] 0.880064183 0.873371125 0.162405146 0.004233302 0.429961786 0.607225944
 [25] 0.751426830 0.174920789 0.037173663 0.055648731 0.399081284 0.015876666
 [31] 0.607480008 0.139448619 0.142724464 0.348229449 0.253615442 0.205885260
 [37] 0.465343422 0.006544791 0.099991179 0.826945701 0.851589145 0.918020321
 [43] 0.463926255 0.013740303 0.547316027 0.225599156 0.633296575 0.883999027
 [49] 0.245247196 0.685669335 0.114173778 0.154435183 0.918742437 0.215483073
 [55] 0.193481369 0.252110722 0.897391131 0.212809555 0.081155536 0.632644066
 [61] 0.917235718 0.328185351 0.642744885 0.136010247 0.681466008 0.437928031
 [67] 0.189861831 0.609069185 0.877659020 0.895820156 0.329262631 0.679087543
 [73] 0.479225250 0.036869199 0.171706127 0.778473611 0.881071749 0.512210809
 [79] 0.266040866 0.530527571 0.149158217 0.698022749 0.673886409 0.623341016
 [85] 0.680057902 0.324141492 0.076018161 0.189576790 0.151097020 0.066818950
 [91] 0.380175331 0.445752973 0.069697813 0.747152596 0.388876913 0.842630115
 [97] 0.788939239 0.495677578 0.335830710 0.758991263

> x <- 0:length(pp)
> x
  [1]   0   1   2   3   4   5   6   7   8   9  10  11  12  13  14  15  16  17  18
 [20]  19  20  21  22  23  24  25  26  27  28  29  30  31  32  33  34  35  36  37
 [39]  38  39  40  41  42  43  44  45  46  47  48  49  50  51  52  53  54  55  56
 [58]  57  58  59  60  61  62  63  64  65  66  67  68  69  70  71  72  73  74  75
 [77]  76  77  78  79  80  81  82  83  84  85  86  87  88  89  90  91  92  93  94
 [96]  95  96  97  98  99 100
 
 
 > pmf <- dpoibin(x, pp)
 > pmf
  [1] 0.000000e+00 2.992243e-19 1.006538e-19 4.643101e-19 0.000000e+00
  [6] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
 [11] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 1.799810e-16
 [16] 1.954107e-15 1.665084e-14 1.282902e-13 9.042169e-13 5.850817e-12
 [21] 3.484866e-11 1.915063e-10 9.729614e-10 4.578480e-09 1.998844e-08
 [26] 8.108083e-08 3.060040e-07 1.075818e-06 3.527262e-06 1.079601e-05
 [31] 3.087559e-05 8.257652e-05 2.066886e-04 4.844999e-04 1.064287e-03
 [36] 2.192074e-03 4.235484e-03 7.680668e-03 1.307731e-02 2.091300e-02
 [41] 3.142167e-02 4.436853e-02 5.889176e-02 7.349404e-02 8.624543e-02
 [46] 9.518298e-02 9.880062e-02 9.646291e-02 8.858703e-02 7.652149e-02
 [51] 6.216994e-02 4.750367e-02 3.413307e-02 2.306014e-02 1.464568e-02
 [56] 8.742287e-03 4.903436e-03 2.583517e-03 1.278252e-03 5.936859e-04
 [61] 2.587351e-04 1.057585e-04 4.052469e-05 1.454886e-05 4.890809e-06
 [66] 1.538462e-06 4.525141e-07 1.243576e-07 3.190302e-08 7.633072e-09
 [71] 1.701479e-09 3.529589e-10 6.805449e-11 1.217984e-11 2.020466e-12
 [76] 3.102147e-13 4.406783e-14 5.832046e-15 7.769900e-16 1.641183e-16
 [81] 9.276405e-17 8.718370e-17 8.530681e-17 7.806161e-17 6.550252e-17
 [86] 3.997567e-17 2.863738e-17 1.576025e-17 5.723475e-18 9.286634e-18
 [91] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
 [96] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
[101] 0.000000e+00

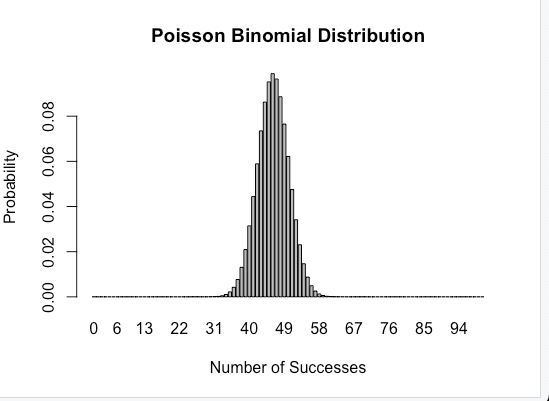
> barplot(pmf, names.arg = x, main = "Poisson Binomial Distribution", xlab = "Number of Successes", ylab = "Probability")