Julia で線形代数① Vector

事前準備

1. Julia のinstall

M1 Mac用コマンド
brew install --cask julia

2. Julia起動
   実行コマンド

julia

結果

               _
   _       _ _(_)_     |  Documentation: https://docs.julialang.org
  (_)     | (_) (_)    |
   _ _   _| |_  __ _   |  Type "?" for help, "]?" for Pkg help.
  | | | | | | |/ _` |  |
  | | |_| | | | (_| |  |  Version 1.9.3 (2023-08-24)
 _/ |\__'_|_|_|\__'_|  |  Official https://julialang.org/ release
|__/                   |

julia>

3. Packageのinstall

実行コマンド

julia>
pkg> add Plots
pkg> add LinearAlgebra
pkg> add SparseArrays

結果

pkg> status
Status `~/.julia/environments/v1.9/Project.toml`
  [91a5bcdd] Plots v1.39.0
  [37e2e46d] LinearAlgebra
  [2f01184e] SparseArrays

4. Packageを使用

julia> using LinearAlgebra, SparseArrays

Vector

Juliaにおけるベクトルは、一次元のArrayオブジェクトで表されます。ベクトルは、要素のリストを[]で囲んで、要素を, または; で区切って指定することで構築されます。length関数はサイズを返します。

julia> x = [ -2.1, 0.0, 7.0, -1.5, 3.2 ]
5-element Vector{Float64}:
 -2.1
  0.0
  7.0
 -1.5
  3.2

julia> length(x)
5

julia>　y = [ -2.1; 0.0; 7.0; -1.5; 3.2 ] #セミコロンでも
5-element Vector{Float64}:
 -2.1
  0.0
  7.0
 -1.5
  3.2
 
julia> length(y)
5

コンマをつけないと行列になります

julia> x = [ -2.1 0.0  7.0  -1.5 3.2 ]
1×5 Matrix{Float64}:
 -2.1  0.0  7.0  -1.5  3.2

JuliaではArrayは1からはじまります。0だとエラー

julia> x[0]
ERROR: BoundsError: attempt to access 5-element Vector{Float64} at index [0]
Stacktrace:
 [1] getindex(A::Vector{Float64}, i1::Int64)
   @ Base ./essentials.jl:13
 [2] top-level scope
   @ REPL[21]:1

julia> x[1]
-2.1

=を使って代入すると基本的には参照になります

julia> x = [ -2.1, 0.0, 7.0, -1.5, 3.2 ]
5-element Vector{Float64}:
 -2.1
  0.0
  7.0
 -1.5
  3.2

julia> y=x
5-element Vector{Float64}:
 -2.1
  0.0
  7.0
 -1.5
  3.2

julia> x[3]=4.0
4.0

julia> y
5-element Vector{Float64}:
 -2.1
  0.0
  4.0
 -1.5
  3.2

julia> x
5-element Vector{Float64}:
 -2.1
  0.0
  4.0
 -1.5
  3.2

julia> y[1]=2.0
2.0

julia> x
5-element Vector{Float64}:
  2.0
  0.0
  4.0
 -1.5
  3.2

copy関数を使うと参照ではなくcopyになります

julia> x = [ -2.1, 0.0, 7.0, -1.5, 3.2 ]
5-element Vector{Float64}:
 -2.1
  0.0
  7.0
 -1.5
  3.2
  
julia> y = copy(x)
5-element Vector{Float64}:
 -2.1
  0.0
  7.0
 -1.5
  3.2

julia> x[3] = 4.0;

julia> y
5-element Vector{Float64}:
 -2.1
  0.0
  7.0
 -1.5
  3.2

#yはコピーでxのみ変更されているので、falseになる
julia> y == x
false

vcat関数を使うと連結できます

julia> x = [ 1, -3 ]
2-element Vector{Int64}:
 1
 -3
 
julia> y = [ 2, 5, 6 ]
3-element Vector{Int64}:
 2
 5
 6

julia> z = vcat(x,y)
5-element Vector{Int64}:
  1
 -3
  2
  5
  6

Vectorを持つlist

julia> x = [ 1.0, 0 ]; y = [ 1.0, -1.0 ]; z = [ 0, 1.0];

julia> list = [ x, y, z ]
3-element Vector{Vector{Float64}}:
 [1.0, 0.0]
 [1.0, -1.0]
 [0.0, 1.0]

zeros(n)でゼロベクトル作成

julia> zeros(2)
2-element Vector{Float64}:
0.0
0.0

Julia inline関数を使って、次元n, i番目の単位ベクトルを作成

julia> unit_vector(i,n) = [zeros(i-1); 1 ; zeros(n-i)]
unit_vector (generic function with 1 method)

julia> unit_vector(3,5)
5-element Vector{Float64}:
0.0
0.0
1.0
0.0
0.0

ones(n)でn次元で全て1のベクトル作成

julia> ones(3)
3-element Vector{Float64}:
1.0
1.0
1.0

rand(n)でn次元のランダムベクトル作成

  julia> rand(2)
2-element Vector{Float64}:
0.5362840580544231
0.6267353630651851  

randn(n)にすると正規分布に従っているn次元のベクトルをランダムで提供します。

randn(3)
3-element Vector{Float64}:
-0.01862640006942847
-0.6767070903788958
-1.191567956516634

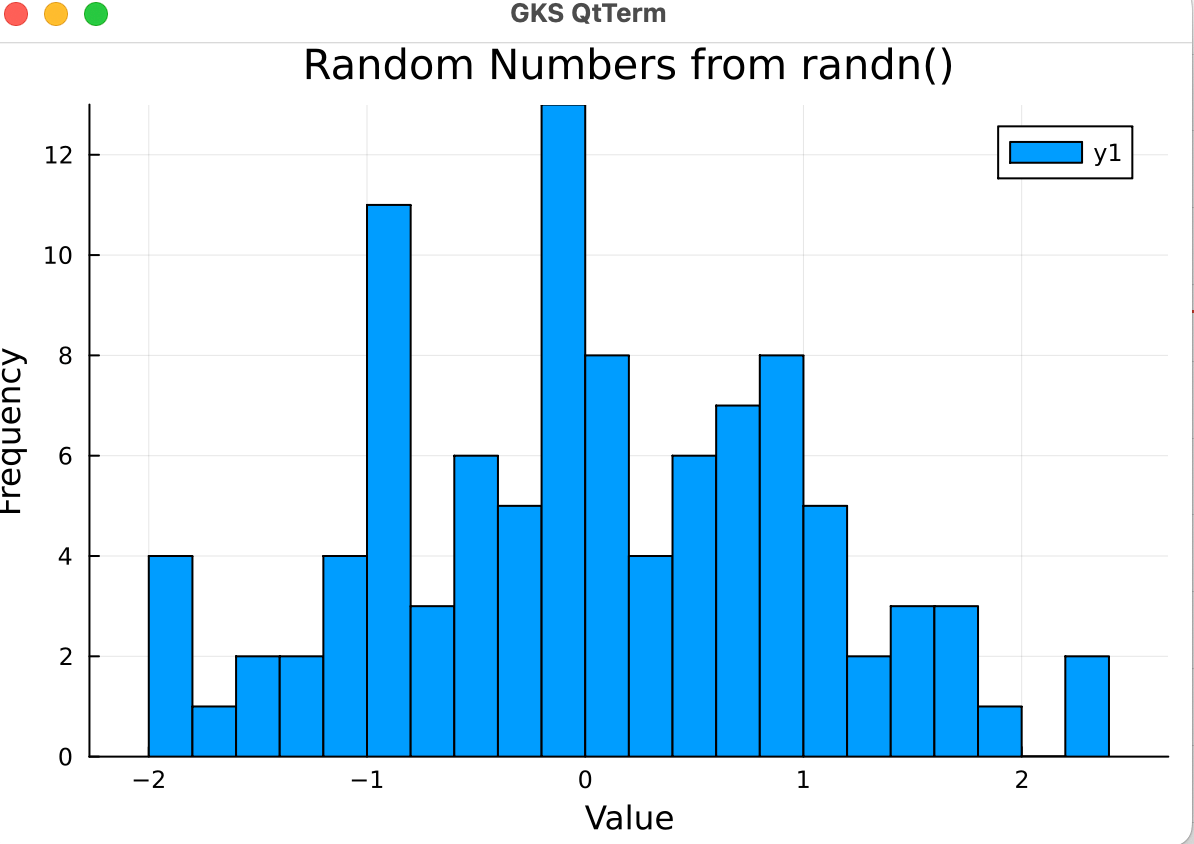
Plotsで可視化しよう

julia> using Plots
julia> n = 100；
julia> random_vector = randn(n);
julia> histogram(random_vector, bins=20, xlabel="Value", ylabel="Frequency", title="Random Numbers from randn()")

Vector演算

足し算

julia> [ 1, 4, 3 ] + [ 1, 2, 4 ]
3-element Vector{Int64}:
 2
 6
 7

引き算

julia> [ 1, 4, 3 ] - [ 1, 2, 4 ]
3-element Vector{Int64}:
  0
  2
 -1

Scalarで掛け算

julia> x = [ 10, 3, -1 ];

julia> 5 * x
3-element Vector{Int64}:
 50
 15
 -5
 
 # 反対にしても結果は一緒
 julia> x * 5 
3-element Vector{Int64}:
 50
 15
 -5

Scalarで割り算

julia> x / 4
3-element Vector{Float64}:
  2.5
  0.75
 -0.25

#反対にして/を\にすると結果は一緒
julia> 4 \ x
3-element Vector{Float64}:
  2.5
  0.75
 -0.25
 
 反対にしたままだと違う計算に
 julia> 4 / x
1×3 transpose(::Vector{Float64}) with eltype Float64:
 0.363636  0.109091  -0.0363636

x .+ a. でscalar aとvector xを足し算

julia> x = [1,2,3]
3-element Vector{Int64}:
 1
 2
 3

julia> a = -1
-1

julia> x .+a
3-element Vector{Int64}:
 0
 1
 2
 
 julia> x .-a
3-element Vector{Int64}:
 2
 3
 4

要素ごとの演算
演算子の前にピリオドまたはドットを追加する。例えば、xとyが同じ長さのベクトルである場合、x.*y、x./y、x.\y、x.^yは要素ごとの演算です。これらはxとyと同じ長さのベクトルを生成し、それぞれi番目の要素はxiyi、xi/yi、yi/xi、およびxiyi^iになる。

julia> x = [1.0, 2.0, 3.0, 4.0];
julia> y = [5.0, 6.0, 7.0, 8.0];
# 要素ごとの乗算（xとyの各要素同士を掛け算）
julia> x .* y 
4-element Vector{Float64}:
  5.0
 12.0
 21.0
 32.0
# 要素ごとの除算（xとyの各要素同士を割り算）
julia> x ./ y 
4-element Vector{Float64}:
 0.2
 0.3333333333333333
 0.42857142857142855
 0.5

# 要素ごとのべき乗（xの各要素をyの各要素乗算） 
julia> x .^ y
4-element Vector{Float64}:
     1.0
    64.0
  2187.0
 65536.0

関数にもピリオドが使える

julia> x = [0.0, π/2, π, 3π/2]
# sin関数を要素ごとに適用
julia> sine_values = sin.(x)
4-element Vector{Float64}:
  0.0
  1.0
  1.2246467991473532e-16
 -1.0
 
 # 2つのベクトルを作成
julia> a = [1, 2, 3];
julia> b = [1, 3, 3];

# 等号テスト演算子を要素ごとに適用
julia> elementwise_equality = a .== b
3-element BitVector:
 1
 0
 1

線形結合

# ベクトルを定義
julia> a = [1.0, 2.0, 3.0];
julia> b = [4.0, 5.0, 6.0];

# スカラー係数を定義
julia> alpha = 2.0;
julia> beta = 3.0;

# 線形結合を計算
julia> linear_combination = alpha * a + beta * b
3-element Vector{Float64}:
 14.0
 19.0
 24.0

内積

n-ベクトルxとyの内積x^T yは。x'*y

julia> x = [1,2,3];

julia> y = [2,0,10];

julia> x'*y
32

疎なベクトル

SparseArraysで疎なベクトルを作成、操作する
Juliaでは、sparsevec関数を使用して、インデックスと値のリストから疎なベクトルを作成できる。また、最初にゼロの疎なベクトル（spzeros(n)を使用して）を作成し、その後ゼロでないエントリに値を割り当てることも可能。非疎なベクトルから疎なベクトルを作成するにはsparse(x)を使用し、xの疎なバージョンを返す。nnz(x)は疎なベクトルのゼロでない要素の数を返す。疎なベクトルは、通常のベクトル操作と同じように動作するようにオーバーロードされており、適切な場合には非疎なベクトルとして自動的に再キャストされる。

julia> a = sparsevec( [ 123456, 123457 ], [ 1.0, -1.0 ], 10^6 )
1000000-element SparseVector{Float64, Int64} with 2 stored entries:
  [123456]  =  1.0
  [123457]  =  -1.0
  
julia> length(a)
1000000

julia> nnz(a)
2

#疎ではないベクトルbを作成し、a, bの計算効率比較
julia> b = randn(10^6);
julia> @time 2*a;
  0.000010 seconds (3 allocations: 192 bytes)
julia> @time 2*b;
  0.001327 seconds (2 allocations: 7.629 MiB)