Zenn
⚗️

クローズドLLM (GPT, Gemini, Claude, etc.)からの知識蒸留 [論文より]

に公開
AI
論文
LLM
生成 AI
知識蒸留
tech

はじめに

LLMって、どうやって知識蒸留(Knowledge Distillation: KD)するんだろう、ふと疑問に思いました。
arXivを探してたところ、サーベイ論文を発見したので読んでみました。
そのメモを残していきます。

調査のきっかけ

LLMをKDしようと思ったときに、2パターンあると思います。

  1. Open Source（Open Weight）モデルから蒸留する場合
  2. Closed Source (Proprietary)モデルから蒸留する場合

[2]によると、1の場合はAttention行列を模倣することがよくあるそうです。Attension行列には文法に基づいた注意パターンを表しており、それを真似することで効果的に暗黙知(dark knowledge)を学習できるとのこと。
確かにオープンソースであれば好きな箇所の出力を取得することができるので、特徴蒸留もできますし、たしかにうまくいきそうな感じがします。
では、2の場合はどうでしょう。Closed Sourceモデル（GPT-4、Claude、Geminiなど）からKDする場合、Open Sourceモデルとは大きく異なるアプローチが必要になります。前述のようにオープンソースモデルではAttention行列などの内部表現にアクセスできますが、独自モデルではそれらの内部状態にアクセスできないため、別の戦略が求められます。

単純に考えると、Closed Sourceモデルに与えたInputとそのOutputを元に、生徒モデルを学習させることになります（それしかできなさそうですね）。
果たして、その方法はうまくいくのでしょうか？
論文[1]を調査し、どのような方法があるのか調べてみました。

論文[1]の調査結果

1. イントロダクション（モチベーション）

[1]の1. INTRODUCTIONの内容です。

Closed Sourceモデルには、アクセス制限と高コスト、そしてデータプライバシーとセキュリティの観点での懸念という欠点がある。
対象的に、Open Sourceモデルは、制限や（インフラがあれば）コストの支払いなしに使用できるのに加えて、AI研究の促進にも貢献する。

しかし、性能的にはどうしてもClosed Sourceモデル > Open Sourceモデルとなっているのが現実である。この性能格差を埋める手段として知識蒸留(KD)の手法の研究が進んでいる。


KDはLLMにおいて3つの重要な役割を果たす([1]のFigure 1)。
①性能の向上
②効率性のための規模圧縮(compression)
③自己生成知識(self-generated knowledge)による自己改善(Self-Improvement)

論文[1]によると、一連の蒸留技術を通じて、Closed SourceモデルとOpen Sourceモデルの間のギャップは、大幅に狭まっているとのことです。


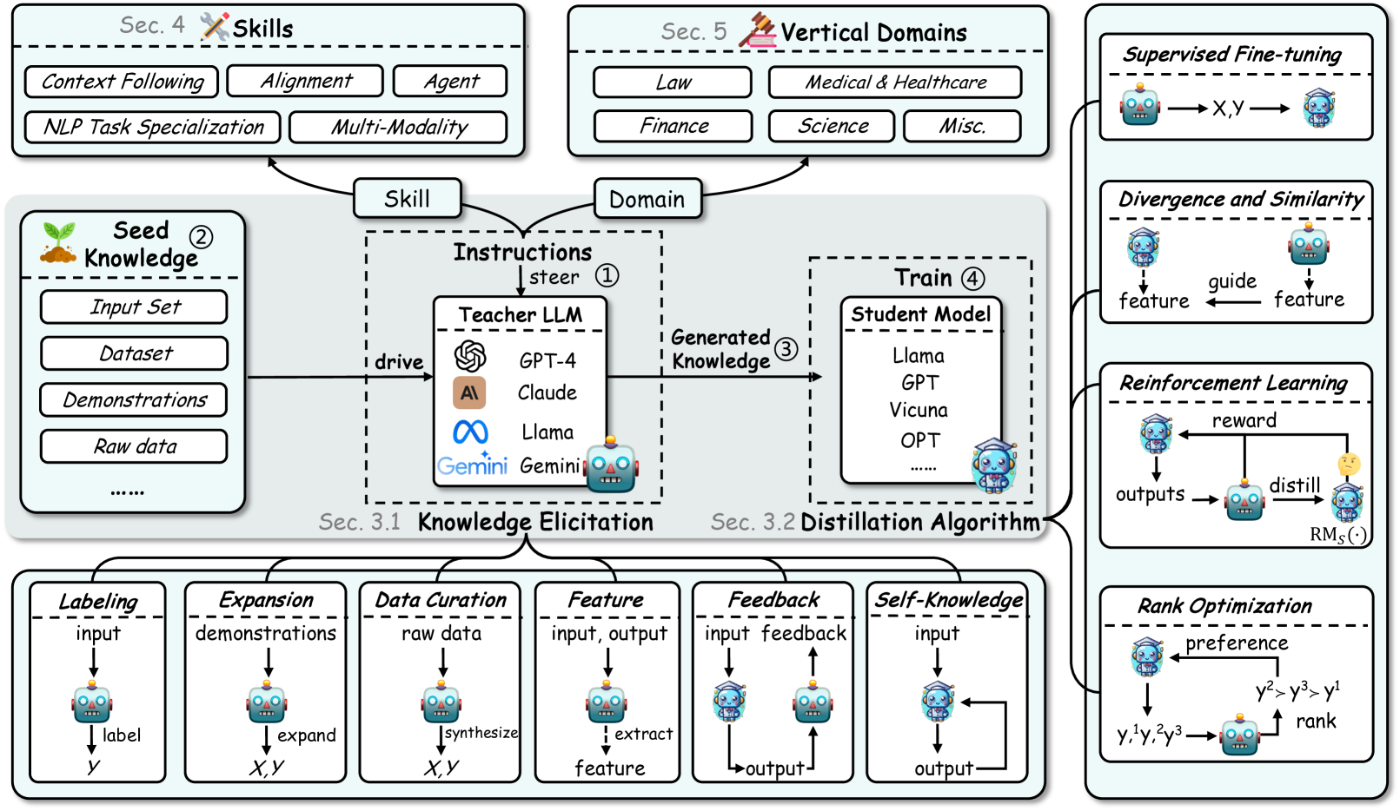
[1]のFigure 2には本論文における調査の構成と、LLMにおけるKDのステップ①→②→③→④が示されています。

本記事では、2章の知識蒸留の概要、3章の知識を引き出す手法(Knowledge Elicitation)と蒸留アルゴリズム(Distillation Algorithm)についてまとめたいと思います。

知識蒸留の概要

[1]の2. OVERVIEWの内容です。

従来の蒸留から、LLMの蒸留へ

AI分野における蒸留とは、大規模で複雑なモデル（教師モデル）から、小規模で効率的なモデル（生徒モデル）へ知識を転移するプロセスを指していた。
しかしLLMの出現により状況は変わりました。GPT-4やGeminiなどのClosed Sourceモデルには、我々はパラメータにアクセスできないためで、プルーニングや量子化を使用して圧縮することが困難です。そこで、知識蒸留の目的としては、単なるアーキテクチャの圧縮から知識の引き出しと転移と、焦点をシフトしていったそうです。

この「知識を引き出し転移する」アプローチの鍵は、プロンプトです。プロンプトは、自然言語理解から推論や課題解決などのより複雑な認知タスクまで、様々な領域におけるLLMの理解と能力を活用するように設計されます。この工夫により、特定のスキルや関心領域に焦点を当てた、より的を絞った知識の抽出を可能にしているそうです。

Data Augmentation (DA)

DAは、LLMの知識蒸留において必要不可欠な要素になりつつあるそうです。
従来はparaphrasing (ある１データの意味とできるだけ同じになるように、新たなデータを作成する手法)やback-translation (元のテキストを他の言語に翻訳し、その翻訳したテキストを再び元の言語に翻訳することで、新たなデータを生成する方法)などの手法で、機械的にデータを拡張していました。
しかし、LLMのコンテキストにおけるDAは、特定のドメインやスキルに合わせた新しいコンテキストリッチなトレーニングデータの生成に焦点を当てています。

LLM時代の蒸留パイプライン

強い教師モデルから、より単純な生徒モデルへ知識を転移することを目的としたプロセスを紹介します。このパイプラインは、GPT-4やGeminiなどのClosed Sourceモデルの高度な能力を、よりアクセスしやすく効率的なOpen Sourceモデルの対応物で活用するために不可欠です。このパイプラインの概要は、知識蒸留において重要な役割を果たす4つの明確な段階に大きく分類できます([1]のFigure 4)。

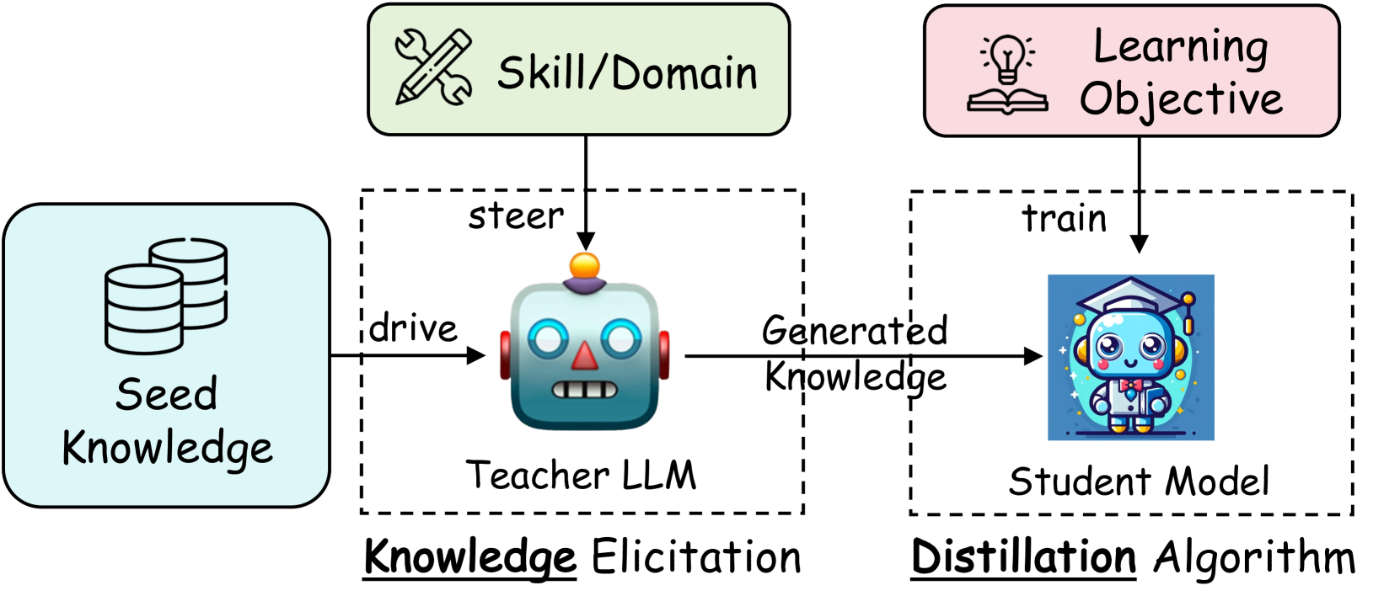
  1. ターゲットのスキル/ドメインに基づく、教師LLMのステアリング
    教師LLMの出力を、特定のターゲットスキルまたはドメインに向けるために指示を出す。例えば、システムプロンプトなどで実行される。

  2. インプットとしてのシード知識を収集
    教師LLM提供するためのシード知識(特定の分野やスキルに関連する基本的な情報や初期データセット)を収集する。

  3. 蒸留知識の生成
    ステアリングとシード知識に応じて、教師LLMに知識例を生成させる。これらの例は主にQA対話形式や語り口調の説明形式となる。

  4. 特定の学習目標を持つ生徒モデルのトレーニング
    生成された知識例を使用して生徒モデルをトレーニングする。このトレーニングには学習目標に合わせた損失関数が定義され、損失関数を最小化することで学習する。

上記の1～4のステージは、下記の2式に定式化できますね。

\mathcal{D}_I^{(\text{kd})} = \{\text{Parse}(o, s)|o \sim p_T(o|I \oplus s), \forall s \sim \mathcal{S}\}

ここで、\oplusはテキストの結合、Iはステアリングのためのインストラクションプロンプト、s \sim \mathcal{S}はシード知識です。oは教師LLMのアウトプット(蒸留例)であり、\text{Parse}(o, s)は蒸留例をパース(学習しやすい形に）しています。p_Tはパラメータ\theta_Tを持つ教師LLMです。このようにして作成された知識蒸留のためのデータセット\mathcal{D}_I^{(\text{kd})}が与えられます。

上記の式は、言葉で書くと、シード知識郡\mathcal{S}からサンプリングされたシード知識sと、インストラクションIを教師LLMに与えて出力されたoを、何らかの形にパースして知識蒸留データセット\mathcal{D}_I^{(\text{kd})}に蓄える、という解釈になります。

次に損失関数です。

\mathcal{L} = \sum_I \mathcal{L}_I(\mathcal{D}_I^{(\text{kd})}; \theta_S)

ここで、\sum_Iは生徒モデルに複数のタスクまたはスキルが蒸留される可能性があることを表し、\mathcal{L}_I()は特定のドメインやスキルに対する損失関数を表します。また、\theta_Sは生徒モデルのパラメータです。

本論文では、LLM時代に目立った特定の蒸留について紹介するそうです。

上記（[1]のFigure 5)は、教師LLMからの知識の引き出し方を表しています（詳しくは次の章で説明されます）。

  • Labeling: 教師モデルが入力から出力を生成する
  • Expansion: 教師モデルが文脈内学習を通じて、与えられた例示に似たサンプルを生成する
  • Data Curation: 教師モデルがトピックやエンティティなどのメタ情報に基づいてデータを合成する
  • Feature: データを教師モデルに入力し、ロジットや特徴などの内部知識を抽出する (抽出できる場合に限る)
  • Feedback: 教師モデルが生徒モデルの生成に対して、好み、修正、難しいサンプルの拡張などのフィードバックを提供する
  • Self-Knowledge: 生徒モデルが最初に出力を生成し、それが高品質のものにフィルタリングされるか、生徒モデル自身によって評価される

知識を引き出す手法

[1]の3.1. Knowledgeの手法です。

Labeling

Labelingとは、教師LLMを使用して、インストラクションI、いくつかのデモンストレーション（few shotにあたる。入力例と回答例をいくつか渡す。）cに従って、与えられた入力xに対する出力yを取得する方法です。
最もシンプルな割に効果的で、広く適用されているそうです。

\mathcal{D}^{(\text{lab})} = \{x, y|x \sim \mathcal{X}, y \sim p_T(y|I \oplus c \oplus x)\}

数式もシンプルですね。xは既存のNLPタスクデータセット\mathcal{X}から取得することができ、お手軽です。Iとcとxをつなげたプロンプトを教師モデルp_Tに渡してyを得て、それを(x, y)のペアとしてデータセットに保管してます。
指示Iやcなどに、CoTプロンプトを渡し、多くの出力を得る、という工夫もされているそうです。

Expansion


Labelingのアプローチは、入力データが多様性を持つものでないと、うまくはたらきません。この制約に対処するために、様々な拡張方法が提案されています。大まかな流れは、デモンストレーションcをシード知識として使用し、コンテキスト内学習（いわゆるfew shot）によって大規模で多様なデータに拡張することを目的としています。

\mathcal{D}^{(\text{exp})} = \{(x, y)|x \sim p_T(x|I \oplus c), y \sim p_T(y|I \oplus x)\}

I \oplus xからの出力yは普通のように思えますが、その入力xがI \oplus cを入力とした教師LLMのoutputから生成されているところが、Labelingと異なります（LabelingはNLPタスクデータセット\mathcal{X}からサンプリングしていた）。

ExpansionはLLMのコンテキスト内学習の強みを活用して、入力と出力の両方を持つより多様で広範なデータセットを生成します。ただし、生成されたデータの品質と多様性は、教師LLMと初期シード知識に大きく依存するという問題点があります。このことは、教師LLMから固有のバイアスを持つデータセットが生成されやすくなったり、アウトプットxが類似性を持ちやすいという同質性の問題につながる可能性があり、Expansionの目的である多様性を制限します。

Data Curation

Data Curationは、LabelingとExpansionの課題である、多様性の確保を解決するために考案されました。

\mathcal{D}^{(\text{cur})} = \{(x, y)|x \sim p_T(x|I \oplus m), y \sim p_T(y|I \oplus x)\}

Data Curationは、トピックや知識ポイントなどの多様なメタ情報mをプロセスに組み込んで、制御可能な x と y を生成します。入力xがI \oplus mから生成されていますね。

このメタ情報には何を使うのか、は研究によって異なるそうです。
1つは、広範なメタ情報を使用する方法です。例えば「テクノロジー」や「食べ物と飲み物」などの30のメタトピックを使用して、幅広い指示と会話を蒸留しています。

もう一方はいわゆる「教科書」のような高品質で小規模なデータセットでの蒸留に焦点を当てています。こちらは例えばコーディングドメインを学習するときに用いられ、Pythonであれば、蒸留されるデータは10億トークンのPython教科書および解答付きの1億8千万トークンのPython演習という量にのぼります。これを使用したモデルは、HumanEvalやMBPPなどのコーディングベンチマークでほぼすべてのオープンソースモデルを上回るパフォーマンスを発揮したそうです。

このようにData Curationは、高品質で多様かつ大規模なデータセットを合成するための有望な技術とされています。

Feature


これまでの手法と異なり、こちらはホワイトボックスモデルに対してのみ行える蒸留方法です。そのためGPTやGeminiなどには適用できません。

\mathcal{D}^{(\text{feat})} = \{(x, y, \phi_{\text{feat}}(x, y; \theta_T)) | x \sim \mathcal{X}, y \sim \mathcal{Y}\}

\mathcal{Y} は出力セットであり、教師モデル、生徒モデルによって生成されるか、データセットから直接取得されます。\phi_{\text{feat}}(\cdot; \theta_T) は教師モデルから特徴知識（出力分布など）を抽出する操作を表します。

この手法は特に小さなモデルで有望性を示しますが、ブラックボックスモデルでは使用できません。さらに、ホワイトボックスな教師モデルよりもブラックボックスの教師モデル（例：GPT-4）がより強力な傾向にあるため、ブラックボックスの同等モデルと比較して性能が劣る可能性があります。

Feedback


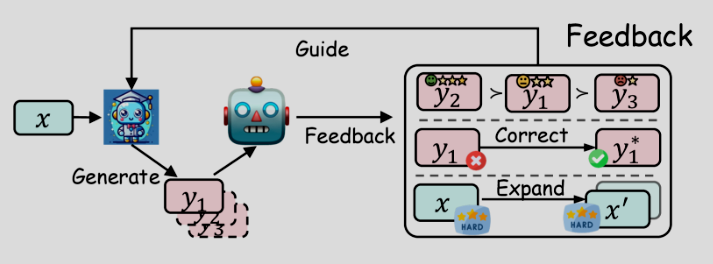
これまでのパイプラインは、主に教師モデルから生徒モデルへの一方向の知識伝達に焦点を当てており、生徒モデルの生成物に対する教師モデルからのフィードバックを考慮していませんでした。教師モデルからのフィードバックは通常、生徒モデルが生成した出力に対する選好、評価、または修正情報を提供することで行われます。例えば、一般的なフィードバック形式として、教師モデルが生徒モデルの生成物をランク付けし、この選好をAIフィードバックからの強化学習（Reinforcement Learning from AI Feedback: RLAIF）を通じて生徒モデルに蒸留することが挙げられます。

\mathcal{D}^{(\text{fb})} = \{(x, y, \phi_{\text{fb}}(x, y; \theta_T))|x \sim \mathcal{X}, y \sim p_S(y|x)\}

ここで、yは入力xに対する生徒モデルp_Sによって生成された出力を表し、\phi_{fb}(\cdot; \theta_T)は教師モデルからのフィードバックを表します。生徒モデルがフィードバックを生成できるようにするだけでなく、生徒モデルがフィードバックに基づいて応答を改善できるようにします。この高度な知識を引き出すためにさまざまな方法が探求されています。

選好のほかにも、生徒モデルの生成物を単に評価するだけでなく、教師モデルは生徒モデルが不十分な部分に対して広範なフィードバックを提供する手法も存在するそうです。

Self-Knowledge


Self-Knowledgeとは、生徒モデル自信から引き出した知識のことです。同じモデルが教師と生徒の両方の役割を果たし、以前に生成した出力を蒸留・改良することで自身を反復的に改善します。この方法では、GPTのような外部の強力な教師モデル（多くの場合はClosed Sourceモデル）の必要性を独自に回避します。

\mathcal{D}^{(\text{sk})} = \{(x, y, \phi_{\text{sk}}(x, y))|x \sim \mathcal{S}, y \sim p_S(y|I \oplus x)\}

ここで、\phi_{\text{sk}}(\cdot)は自己生成出力yに対する追加プロセスを表す一般化関数であり、フィルタリング、報酬付け、またはその他yを強化または評価するメカニズムを指します。要するにそのまま出力yを使うのではなく、学習しやすいように整形するのですね。これは外部ツールまたは生徒モデル自身\theta_Sによって整形されます。この分野の最近の研究では、Self-Knowledgeを引き出すためのさまざまな方法論が提案されており、より効率的で自律的な学習システムを作成する可能性を示しています。

蒸留アルゴリズム

Supervised Fine-Tuning: SFT

SFTは、ブラックボックスLLMを蒸留するための最もシンプルかつ効果的な方法の1つです。SFTは教師モデルによって生成されたシーケンスの尤度を最大化することで生徒モデルをFine-Tuningし、生徒モデルの予測を教師の予測に合わせます。
損失関数は下記となります。

\mathcal{L}_{SFT} = \mathbb{E}_{x \sim \mathcal{X}, y \sim p_T(y|x)} [ -\log p_S(y|x) ]

ここでyは教師モデルによって生成された出力シーケンスです。

Divergence and Similarity

ここでの手法は、主にホワイトボックスである教師モデルから特徴蒸留をするためのアルゴリズムです。これらは、大きく2グループに分類できます。

  • 確率分布のDivergenceを最小化すること
  • 隠れ層の類似性を高めること

確率分布のDivergenceの最小化

損失関数は下記で表されます。

\mathcal{L}_\text{Div} = \mathbb{E}_{x \sim \mathcal{X}, y \sim \mathcal{Y}} [ D( p_T(y | x), p_S(y | x)) ]

Dの具体的な形式は、使用されるDivergenceのタイプによって異なります。例えば、一般的に使用されるDの形式は、Kullback-Leibler Divergence（KLD）であり、それを最小化する、すなわちp_Tとp_Sの出力を同じにすることと同義です。

隠れ層の類似性(Similarity)を高める

Similarity-basedの手法は、生徒モデルの隠れ状態または特徴マップを教師モデルのもとの整合させることを目的としています。
損失関数は下記となります。

\mathcal{L}_{Sim} = \mathbb{E}_{x\sim\mathcal{X},y\sim\mathcal{Y}}[\mathcal{L}_F(\Phi_T(f_T(x,y)),\Phi_S(f_S(x,y)))]

ここでf_T(x,y)とf_S(x,y)はそれぞれ教師モデルと生徒モデルの特徴マップです。変換関数\Phi_Tと\Phi_Sはこれらの特徴マップに適用され、同じ形状になるようにして直接比較を可能にします(FitNetでもこのような変換関数が見られますね)。
類似性関数\mathcal{L}_Fは、これらの変換された特徴マップをマッチングするために使用されます。\mathcal{L}_Fには例えば、L1ノルム、L2ノルム、クロスエントロピーなどを用いるようです。

現状、LLMの知識蒸留においては、Similarity-basedのものはかなり少ないようです。

強化学習

強化学習を用いて教師モデルから生徒モデルへ知識を蒸留する方法が紹介されています。

まずは報酬モデルの訓練です。これは、教師モデルによって作成されたフィードバックデータ\mathcal{D}^{(\text{fb})} (上の方で解説したもの) を使用して報酬モデルr_\phiを訓練します。報酬モデルの損失関数は下記です。

\mathcal{L}_{\mathrm{RM}}(r_{\phi}, \mathcal{D}^{(\mathrm{fd})}) = - \mathbb{E}_{(x,y_w,y_l) \sim \mathcal{D}^{(\mathrm{fd})}} [\log \sigma (r_{\phi} (x, y_w) - r_{\phi} (x, y_l))]

ここで、y_w、y_lはそれぞれ"winning"と"losing"のアウトプットを指します。これは一般的な報酬モデルの損失関数ですね。この損失関数が意味するところとしては、

r_{\phi} (x, y_w) - r_{\phi} (x, y_l)を正にしたい
↓
そうすれば\sigma(\cdot)が1に近づく
↓
そうすれば\logが0に近づく
↓
そうすれば- \mathbb{E}が小さくなる

ということで、y_wに対しては高い報酬を、y_lに対しては低い報酬を返すように学習するのでした。
報酬モデルができたら、それを用いて下記のように期待値を最大化します。

\max_{\pi_\theta} \mathbb{E}_{x \sim X, y \sim \pi_\theta(y|x)} [r_\phi(x,y)] - \beta D_{\mathrm{KL}} [\pi_\theta(y|x) \| \pi_{\mathrm{ref}}(y|x)]

これは、訓練された報酬モデルに従って期待報酬を最大化するように最適化されます。ただし、それだけでは学習データに過学習してしまうので、同時に、- \beta D_{\mathrm{KL}} [\pi_\theta(y|x) \| \pi_{\mathrm{ref}}(y|x)]をすることで、初期段階の生徒モデル\pi_{\mathrm{ref}}と大きく分布が変わらないように制御していますね。

強化学習については、こちらでも解説しています。
https://zenn.dev/barukan300/articles/32bac2a1015b58

ランク最適化

こちらは強化学習に変わる手法です。例えばDPOというものがあります。
DPOについては下記で解説していますので、そちらを参照ください。
https://zenn.dev/barukan300/articles/e16f4b1de300a5

さいごに

今回は"A Survey on Knowledge Distillation of Large Language Models"という論文の1～3章まで見て、いかにClosed Sourceモデルから（一部Open Sourceモデルから）知識を蒸留するかという手法を見てきました。

この論文には4～6章もありますので、機会があればぜひ読んでみたいと思います！

参考文献

[1] Xiaohan Xu, Ming Li, Chongyang Tao, Tao Shen, Reynold Cheng, Jinyang Li, Can Xu, Dacheng Tao, Tianyi Zhou "A Survey on Knowledge Distillation of Large Language Models" arXiv:2402.13116v4, 2024
https://arxiv.org/abs/2402.13116

[2] 佐藤竜馬. 深層ニューラルネットワークの高速化 (第5章). 技術評論社. 2022
https://gihyo.jp/book/2024/978-4-297-14309-1

[3] 岡谷貴之. 深層学習　改訂第2版 (10章). 講談社. 2022
https://www.kspub.co.jp/book/detail/5133323.html

Discussion